禁止转载,来源:totuma.cn
1.3 时间复杂度
🧭 时间复杂度-时间增长趋势
💡 提示
时间复杂度分析统计的不是算法运行时间,而是算法运行时间随着数据量变大时的增长趋势。
通过下面的代码来了解什么是增长趋势
抛开硬件和运行环境等其它影响因素,我们假设每个语句的执行需要一个固定的单位时间为unit_time。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
// 算法 A 的时间复杂度:常数阶
void FuncA(int n) {
int sum = 0; // 1 * unit_time
sum = (1 + n) * n / 2; // 1 * unit_time
printf("sum = %d", sum); // 1 * unit_time
}
// 算法 B 的时间复杂度:线性阶
void FuncB(int n) {
int sum = 0; // 1 * unit_time
for (
int i = 0; // 1 * unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
sum = sum + i; // n * unit_time
}
printf("sum = %d", sum); // 1 * unit_time
}
// 算法 C 的时间复杂度:常数阶
void FuncC(int n) {
int sum = 0; // 1 * unit_time
for (
int i = 0; // 1 * unit_time
i < 99999999; // 99999999 * unit_time
i++ // 99999999 * unit_time
) {
sum = sum + i; // 99999999 * unit_time
}
printf("%d", 0); // 1 * unit_time
}
// 完整代码:totuma.cn如果执行环境固定,则unit_time就是固定的,那么设$T(n)$为$n$和算法操作数量相关的函数。
算法FuncA:虽然语句sum = (1 + n) * n / 2;看上去和$n$相关,但是其运行时间并不会随着问题输入规模$n$的变化而变化。
$$T(n)= 3 * unit\_time$$所以其运行时间可以看做为常数阶$O(1)$。算法FuncB:使用循环对$0$到$n-1$的数进行累加的算法。循环的执行次数与输入规模$n$成正比。
$$\begin{split} T(n)&=3 * unit\_time + n * unit\_time + n*unit\_time + n*unit\_time \\ &= (1 + 3*n*)unit\_time \end{split}$$ 其运行时间和n相关,称为线性阶$O(n)$算法FuncC:也是一个使用循环进行累加的算法,但循环的终止条件与输入规模$n$无关,而是一个固定值。因此,无论输入的 n 是多少,循环都会执行相同的次数。 $$\begin{split} T(n) &= 3 * unit\_time + 3 * 99999999 * unit\_time \\ &= (1 + 3 * 99999999) * unit\_time \end{split}$$ 所以其也为常数阶$O(1)$
大$O$表示法
时间复杂度是用来估计算法运行时间的一种方法,它表示算法的执行时间与输入规模之间的关系。具体地说,时间复杂度描述了算法的运行时间随着输入规模的增加而增长的趋势。
其形式定义如下:
假设$T(n)$是一个算法关于输入规模$n$的函数,用$O(f(n))$表示算法的时间复杂度,当存在为正的常数$c$和$n_0$,使得对于所有的$n > n_0$,都有$0 ≤ T(n) ≤ c * f(n)$成立时,就可以说算法的时间复杂度是$O(f(n))$。
💡 提示
时间复杂度通常表示的是算法的增长趋势,而不是具体的运行时间。
其中:
$T(n)$表示$n$和算法操作数量相关的函数。
$f(n)$表示算法的运行时间的一个上界(上限),是一个函数。
简而言之,时间复杂度$O(f(n))$表示算法的运行时间与$f(n)$的增长趋势相同,或者说算法的运行时间不会超过$f(n)$的某个常数倍。
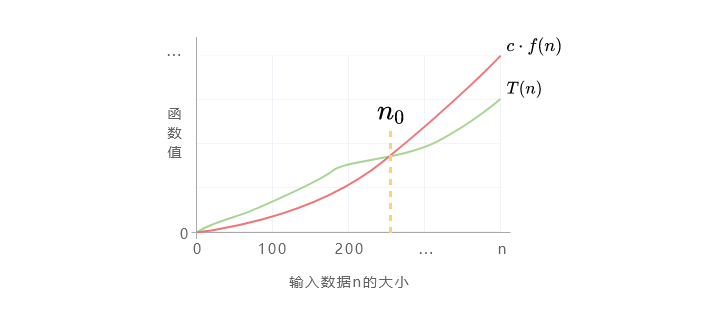
算法 A,B,C 对应增长趋势
通过上述定义我们知道要计算时间复杂度$O(f(n))$首先需要计算操作统计量$T(n)$,其次确认渐进上界$f(n)$。
计算操作统计量$T(n)$
操作统计量是指对算法执行过程中的基本操作进行计数的一种方法,通过统计关键操作的执行次数来分析算法的性能。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
void A (int n) {
int a = 1; // 1 unit_time
a = 2 * a + n; // 1 unit_time
for (
int i = 0; // 1 次
i < 3 * n + 200; // (3 * n + 200) * unit_time
i++ // (3 * n + 200) * unit_time
) {
printf("%d", i); // (3 * n + 200) * unit_time
}
for (
int i = 0; // 1 unit_time
i < 3 * n + 200; // (3 * n + 200) * unit_time
i++ // (3 * n + 200) * unit_time
) {
// 注意,外循环每循环一次,内循环都会循环 (n + 1) 次
// 外循环 总共(3 * n + 200)次,所以内循环应在乘上 (3 * n + 200)
for (
int j = 0; // 1 * (3 * n + 200) unit_time
j < n + 1; // (n + 1) * (3 * n + 200) * unit_time
j++ // (n + 1) * (3 * n + 200) * unit_time
) {
printf("%d", j); // (n + 1) * (3 * n + 200) unit_time
}
}
}
// 完整代码:totuma.cn以上代码的执行次数总和为:
$$\begin{split}T(n)&= 1 + 1 + 1 + 3 * (3 * n + 200) + 1 + 2*(3 * n + 200) + (3 * n + 200) * (1 + 3 * (n + 1) ) \\ &=9n^2 + 627n + 1804 \end{split}$$
2.确认渐进上界$f(n)$
💡 提示
在时间复杂度分析中,常数项和系数通常被省略以简化表达的复杂度,因为它们对于大规模问题来说不是主要的影响因素。主要关注算法的增长趋势,以更好地理解算法在不同输入规模下的性能。
下表展示了一些不同操作数量对应的时间复杂度的例子,其时间复杂度均为最高阶项。
常见的类型
设输入数据的大小为$n$,常见的时间复杂度包括(从低到高顺序排序):
$$O(1)\lt O(\log n) \lt O(n) \lt O(n\log n) \lt O(n^2) \lt O(2^n) \lt O(n!)$$
常数阶 $\lt$ 对数阶 $\lt$ 线性阶 $\lt$ 线性对数阶 $\lt$ 平方阶 $\lt$ 指数阶 $\lt$ 阶乘阶
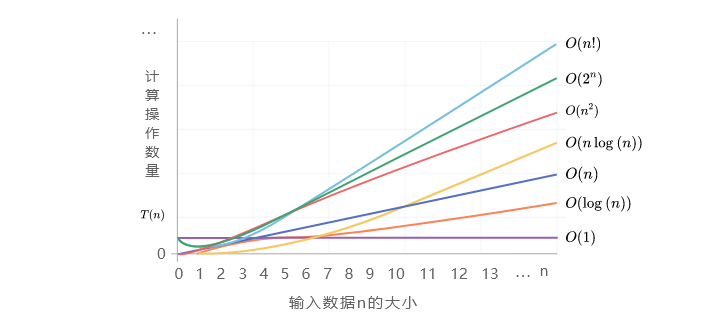
从低到高顺序排序
常数阶时间复杂度$O(1)$
只要我们的程序段执行的时间和输入数据的规模和$n$没有关系,即使需要执行成千上万行代码,那么程序的时间复杂度依旧是$O(1)$。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
// 常数阶
int A () {
int sum = 0; // 1 * unit_time
int i = 0; // 1 * unit_time
int j = 0; // 1 * unit_time
return 0; // 1 * unit_time
}
// 线性阶
int B (int n) {
int count = 0; // 1 * unit_time
for (
int i = 0; // 1 * unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
count++; // n * unit_time
}
return count; // 1 * unit_time
}
// 平方阶
int C (int n) {
int count = 0; // 1 unit_time
for (
int i = 0; // 1 unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
// 注意,外循环每循环一次,内循环都会循环 n 次
// 外循环 总共(3 * n + 200)次,所以内循环应在乘上 (3 * n + 200)
for (
int j = 0; // 1 * n * unit_time
j < n; // n * n * unit_time
j++ // n * n * unit_time
) {
count++; // n * n unit_time
}
}
return count; // 1 unit_time
}
// 完整代码:totuma.cn上述代码段的时间复杂度为: $$\begin{split}T(n)&=4*unit\_time \\&\Longrightarrow f(n)= 4 \\&\Longrightarrow T(n)=O(4)\\& \Longrightarrow O(1)\end{split}$$
线性阶时间复杂度$O(n)$
线性阶的操作数量相对于输入数据大小$n$以线性级别增长。线性阶通常出现在单层循环中:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
// 常数阶
int A () {
int sum = 0; // 1 * unit_time
int i = 0; // 1 * unit_time
int j = 0; // 1 * unit_time
return 0; // 1 * unit_time
}
// 线性阶
int B (int n) {
int count = 0; // 1 * unit_time
for (
int i = 0; // 1 * unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
count++; // n * unit_time
}
return count; // 1 * unit_time
}
// 平方阶
int C (int n) {
int count = 0; // 1 unit_time
for (
int i = 0; // 1 unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
// 注意,外循环每循环一次,内循环都会循环 n 次
// 外循环 总共(3 * n + 200)次,所以内循环应在乘上 (3 * n + 200)
for (
int j = 0; // 1 * n * unit_time
j < n; // n * n * unit_time
j++ // n * n * unit_time
) {
count++; // n * n unit_time
}
}
return count; // 1 unit_time
}
// 完整代码:totuma.cn上述代码的时间复杂度为: $$\begin{split} T(n)&=(1 + 1 + 1) * unit\_time + (n + n + n) * (unit\_time) \\ &=3 * unit\_time + 3n * unit\_time \\ \Longrightarrow f(n) &= 3 + 3n \\ \Longrightarrow O(3 +& 3n) = O(n) \end{split}$$
平方阶时间复杂度$O(n^2)$
平方阶的操作数量相对于输入数据大小$n$以平方级别增长。 平方阶通常出现在嵌套循环中,外层循环和内层循环都为$O(n)$ ,因此总体为$O(n^2)$。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
// 常数阶
int A () {
int sum = 0; // 1 * unit_time
int i = 0; // 1 * unit_time
int j = 0; // 1 * unit_time
return 0; // 1 * unit_time
}
// 线性阶
int B (int n) {
int count = 0; // 1 * unit_time
for (
int i = 0; // 1 * unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
count++; // n * unit_time
}
return count; // 1 * unit_time
}
// 平方阶
int C (int n) {
int count = 0; // 1 unit_time
for (
int i = 0; // 1 unit_time
i < n; // n * unit_time
i++ // n * unit_time
) {
// 注意,外循环每循环一次,内循环都会循环 n 次
// 外循环 总共(3 * n + 200)次,所以内循环应在乘上 (3 * n + 200)
for (
int j = 0; // 1 * n * unit_time
j < n; // n * n * unit_time
j++ // n * n * unit_time
) {
count++; // n * n unit_time
}
}
return count; // 1 unit_time
}
// 完整代码:totuma.cn上述代码的时间复杂度为: $$\begin{split} T(n) &= 3 * unit\_time + 3n * unit\_time + 3n^2 * unit\_time \\ \Longrightarrow f(n) &= 3n^2 + 3n + 3 \\ \Longrightarrow O(3n^2& + 3n + 3) = O(n^2) \end{split}$$
最好、最坏平均时间复杂度
算法的时间效率往往不是固定的,而是与输入的数据有关。
下面给出的代码是在数组(arr)中从头到尾查找目标值(target)。
最好的情况是目标值在数组的头部,那就是常量级的即时间复杂度为$O(1)$。
最坏的情况是目标值在数组的末尾查询了n次才能找到,时间复杂度为$O(n)$。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
// arr 待查找的数组,target 待查找值,n 数组长度
int find(int arr[], int target, int n){
int result = -1;
for(int i = 0; i < n; ++i){
if(arr[i] == target)
return -result;
}
return result;
}
// 完整代码:totuma.cn上述代码中的平均复杂度计算:
一共有 n 种查找到值的情况(可能在第1位查找到,可能第2位....,可能第n位),每一种情况对应的执行次数为 1、2、3……n , 平均复杂度$=\frac{1+2+3+……+n}{n} = \frac{1+n}{2}$,所以平均时间复杂度为$O\left ( n \right )$。