正在载入交互式动画窗口请稍等
BellmanFord(贝尔曼福特) 可视化交互式动画版

假设你有一张地图,地图上不同的城市通过道路连接,每条道路都有一定距离。Bellman -Ford 算法就像一本指南,可以帮助你找到从一个城市到所有其他城市的最短路径,即使有些道路的长度为负数。它就像计算机的GPS,可用于找出网络中从一个点到另一个点的最快路径。在本文中,我们将仔细研究该算法的工作原理以及它为何在解决日常问题时如此方便。
目录
- Bellman-Ford 算法
- Bellman Ford 算法背后的思想
- Bellman-Ford 的边缘松弛原理
- 为什么放松边 N-1 次可以给我们单源最短路径?
- 为什么第N次松弛中距离的减少预示着负循环的存在?
- 使用 Bellman-Ford 算法检测图中的负循环
- 使用 Bellman-Ford 算法查找有向加权图中的负循环
- 处理算法中的不连通图
- Bellman-Ford 算法的复杂度分析
- Bellman Ford 算法的应用
- Bellman Ford 算法的缺点
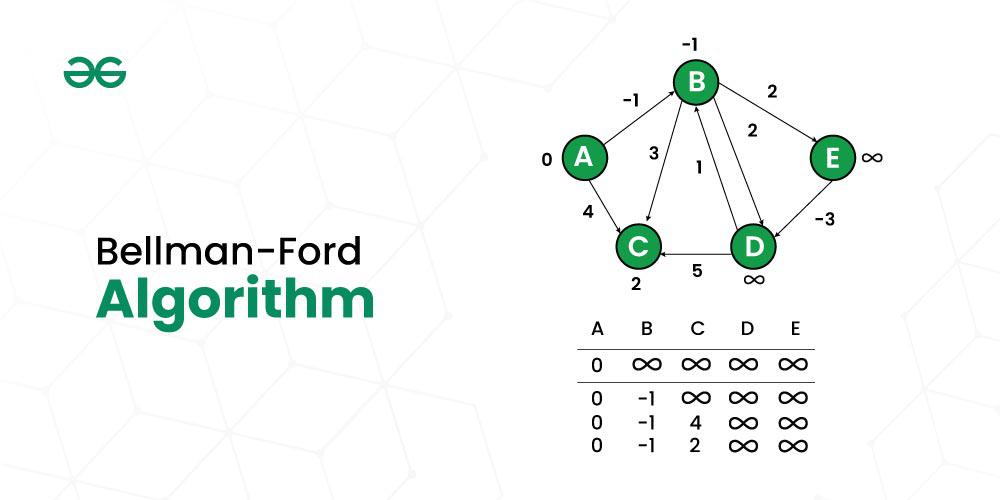
Bellman-Ford 算法
Bellman-Ford是一种单源最短路径算法,用于确定给定源顶点与图中每个其他顶点之间的最短路径。此算法可用于加权和非加权图。
Bellman-Ford算法也能保证找到图中的最短路径,类似于Dijkstra 算法。尽管 Bellman-Ford 算法比Dijkstra 算法慢,但它能够处理具有负边权重的图,这使其更加通用。如果图中存在负循环,则无法找到最短路径。如果我们继续无限次地绕负循环,那么路径的成本将继续下降(即使路径的长度在增加)。因此,Bellman-Ford还能够检测负循环,这是一个重要特性。
Bellman Ford 算法背后的想法:
Bellman-Ford 算法的主要原理是从一个源开始,计算到每个节点的距离。距离最初是未知的,并假设为无限的,但随着时间的推移,该算法通过识别一些较短的路径来放宽这些路径。因此,人们说 Bellman-Ford 是基于“放宽原则”的。
Bellman-Ford 的边缘松弛原理:
- 它指出,对于具有N 个顶点的图,应将所有边放宽N-1次以计算单源最短路径。
- 为了检测是否存在负循环,请再一次放松所有边,如果任何节点的最短距离减少,那么我们可以说存在负循环。简而言之,如果我们将边放松N次,并且第N-1 次和第 N 次放松之间任何节点的最短距离有任何变化,则存在负循环,否则不存在。
为什么放松边 N-1 次可以给我们单源最短路径?
在最坏的情况下,两个顶点之间的最短路径最多可以有N-1条边,其中N是顶点的数量。这是因为在具有N 个顶点的图中,一条简单路径最多可以有N-1条边,因为如果不重新访问顶点,就不可能形成闭环。
通过放宽边N-1次,Bellman-Ford 算法可确保所有顶点的距离估计值都已更新为最佳值(假设图不包含任何可从源顶点到达的负权重循环)。如果图包含可从源顶点到达的负权重循环,则算法可以在N-1次迭代后检测到它,因为负循环会破坏最短路径长度。
总之,在 Bellman-Ford 算法中,将边放宽N-1次可确保算法已探索长度不超过N-1的所有可能路径,这是具有N 个顶点的图中最短路径的最大可能长度。这允许算法正确计算从源顶点到所有其他顶点的最短路径(假设不存在负权重循环)。
为什么第N次松弛中距离的减少预示着负循环的存在?
如前所述,实现到所有其他节点的单源最短路径需要N-1 次松弛。如果第 N 次松弛进一步缩短了任何节点的最短距离,则意味着某条具有负权重的边又被遍历了一次。值得注意的是,在N-1 次松弛期间,我们假设每个顶点只被遍历一次。然而,第 N 次松弛期间距离的缩短表示重新访问了顶点。
使用Bellman-Ford算法检测图中的负循环:
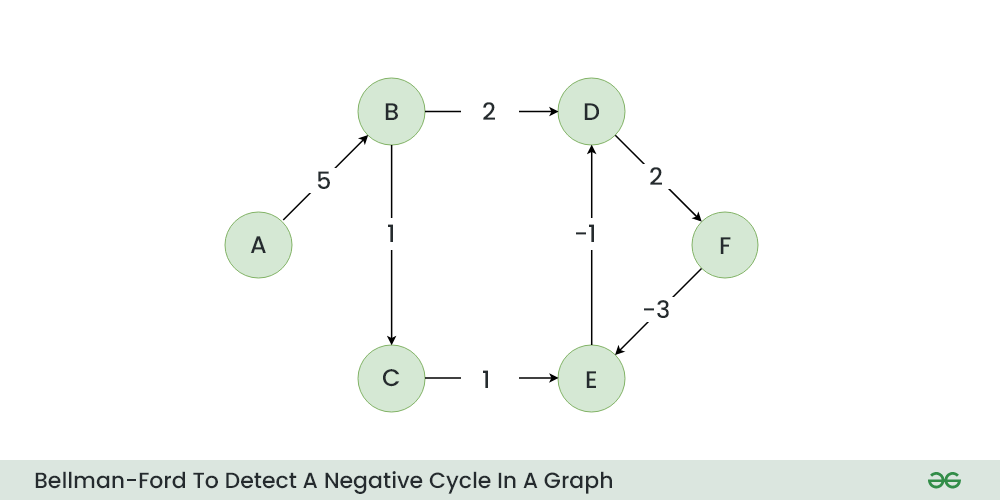
假设我们有如下所示的图表,我们想使用 Bellman-Ford 来查找是否存在负循环。
初始图表
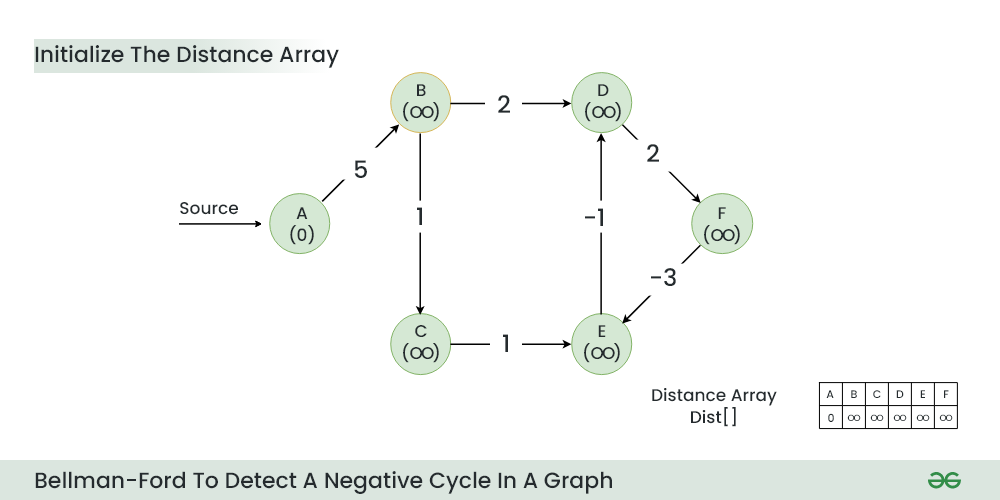
步骤 1:初始化距离数组 Dist[],用于存储每个顶点与源顶点之间的最短距离。最初源顶点的距离为 0,其他顶点的距离为无穷大。
初始化距离数组
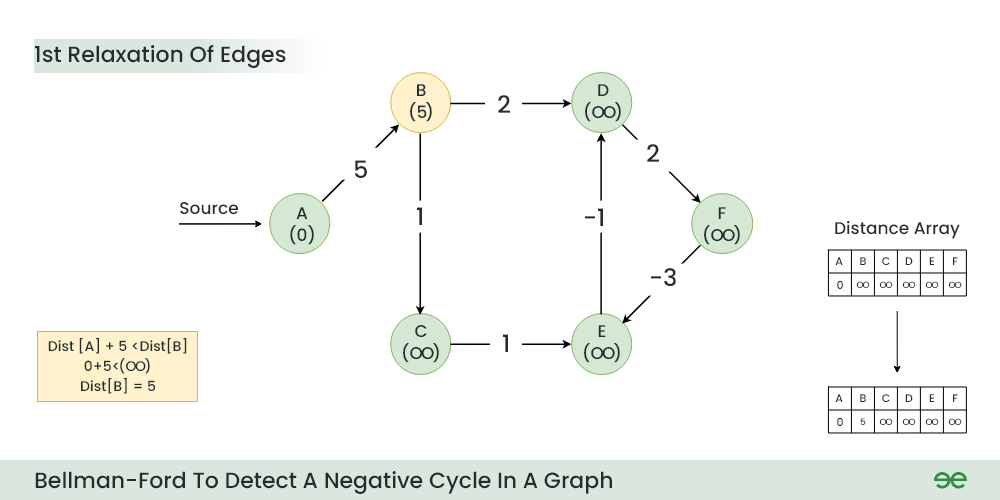
第 2 步:在第一次放松期间开始放松边缘:
- B 的当前距离 > (A 的距离) + (A 到 B 的权重),即无穷大 > 0 + 5
- 因此,Dist[B] = 5
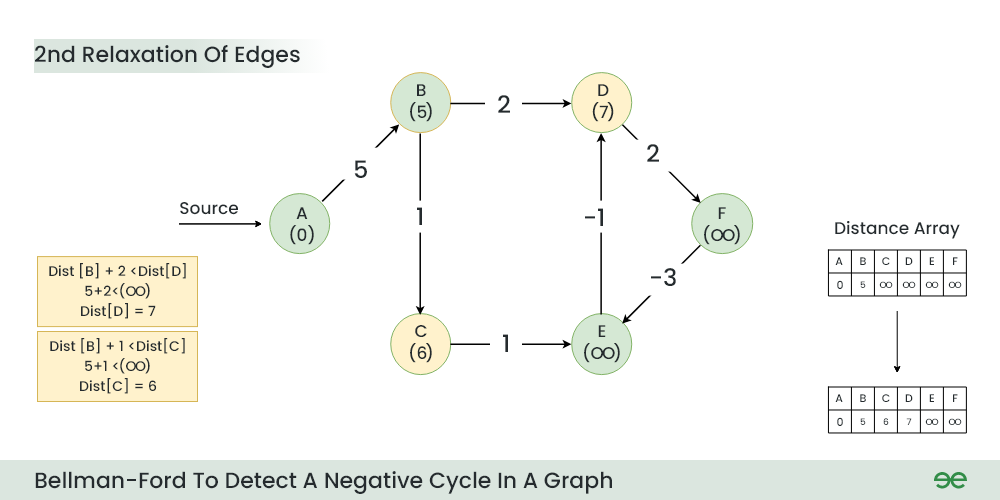
步骤 3:第二次放松时:第一次放松
- D 的当前距离 > (B 的距离) + (B 到 D 的权重) 即无穷大 > 5 + 2
- 距离[D] = 7
- C 的当前距离 > (B 的距离) + (B 到 C 的权重),即无穷大 > 5 + 1
- 距离[C] = 6
第二次放松
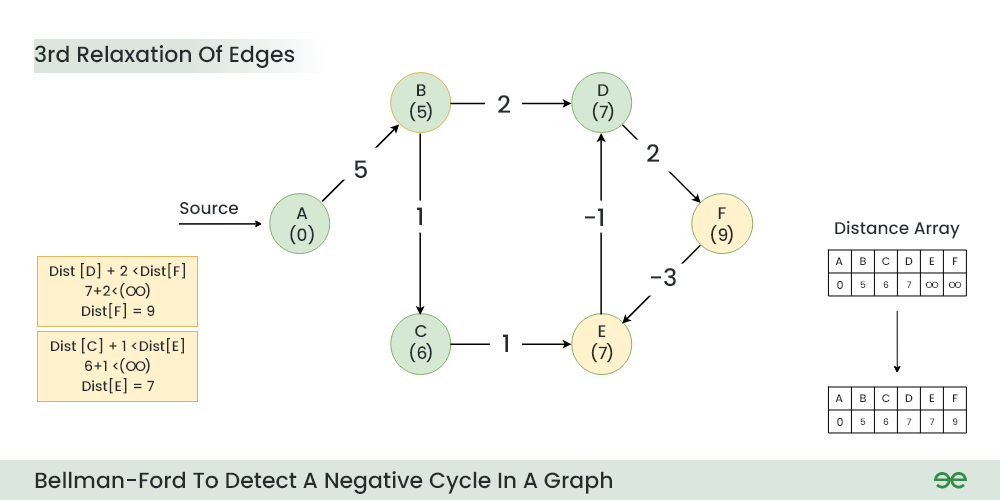
步骤 4:第三次放松时:
- F 的当前距离 > (D 的距离) + (D 到 F 的权重),即无穷大 > 7 + 2
- 距离[F] = 9
- E 的当前距离 > (C 的距离) + (C 到 E 的权重),即无穷大 > 6 + 1
- 距离[E] = 7
第三次放松
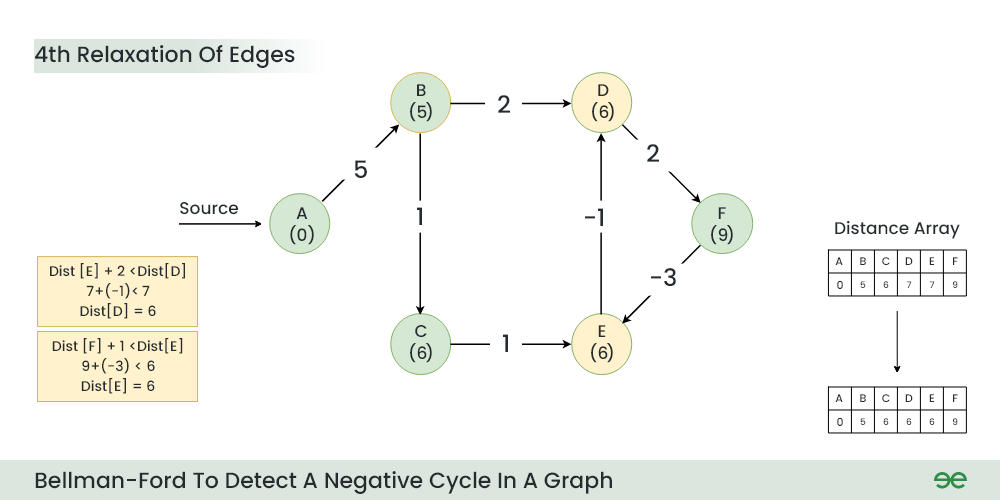
步骤5:第四次放松时:
- D 的当前距离 > (E 的距离) + (E 到 D 的权重) 即 7 > 7 + (-1)
- 距离[D] = 6
- E 的当前距离 > (F 的距离) + (F 到 E 的权重) 即 7 > 9 + (-3)
- 距离[E] = 6
第四放松
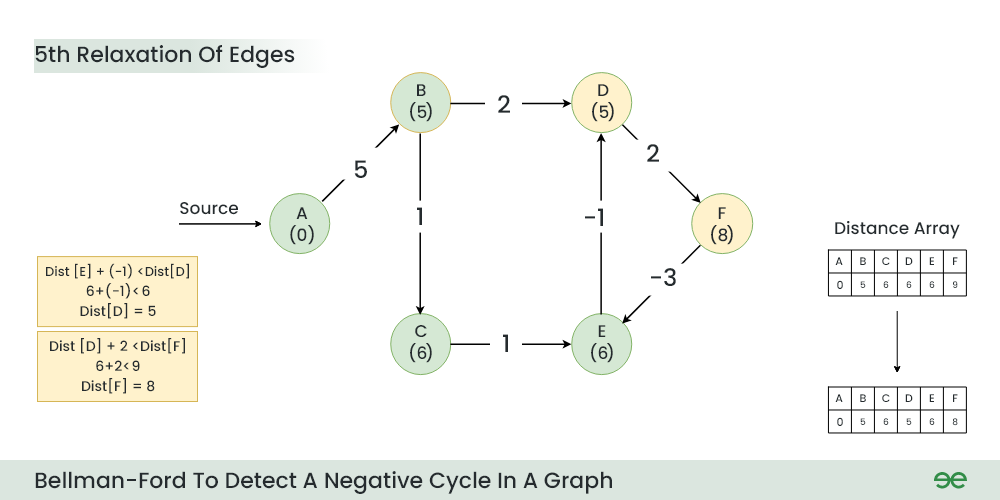
步骤 6:第五次放松时:
- F 的当前距离 > (D 的距离) + (D 到 F 的权重),即 9 > 6 + 2
- 距离[F] = 8
- D 的当前距离 > (E 的距离) + (E 到 D 的权重) 即 6 > 6 + (-1)
- 距离[D] = 5
- 由于图有 6 个顶点,因此在第 5 次松弛期间应该计算出所有顶点的最短距离。
第五放松
步骤 7:现在,最后的放松,即第 6 次放松,如果第 5 次放松的距离数组有任何变化,则应该指示存在负循环。
在第6次放松时,可以看到以下变化:
- E 的当前距离 > (F 的距离) + (F 到 E 的权重) 即 6 > 8 + (-3)
- 距离[E]=5
- F 的当前距离 > (D 的距离) + (D 到 F 的权重),即 8 > 5 + 2
- 距离[F]=7
因为我们观察到距离数组的变化,因此我们可以得出图中存在负循环的结论。
第六次放松
结果:图中存在负循环(D->F->E)。
使用 Bellman-Ford 在有向加权图中查找负循环的算法:
- 为每个顶点 ' v '初始化距离数组 dist[]为dist[v] = INFINITY。
- 假设任何顶点(假设为“0”)作为源并分配dist = 0。
- 根据以下条件放松所有边(u,v,权重)N-1次:
- dist[v] = 最小值(dist[v],距离[u] + 权重)
- 现在,再次放松所有边,即第 N次,并基于以下两种情况,我们可以检测负循环:
- 情况 1(存在负循环):对于任何边(u,v,权重),如果 dist[u] + weight < dist[v]
- 情况 2(无负循环):情况 1 对于所有边均失败。
处理算法中的不连通图:
如果给定的图是不连通的,则上述算法和程序可能无法工作。当所有顶点都可以从源顶点0到达时,它才有效。
为了处理不连通的图,我们可以对距离 = INFINITY 的顶点重复上述算法,或者仅对未访问的顶点重复上述算法。
下面是上述方法的实现:
// A C++ program for Bellman-Ford's single source
// shortest path algorithm.
#include <bits/stdc++.h>
using namespace std;
// a structure to represent a weighted edge in graph
struct Edge {
int src, dest, weight;
};
// a structure to represent a connected, directed and
// weighted graph
struct Graph {
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
struct Edge* edge;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
// A utility function used to print the solution
void printArr(int dist[], int n)
{
printf("Vertex Distance from Source\n");
for (int i = 0; i < n; ++i)
printf("%d \t\t %d\n", i, dist[i]);
}
// The main function that finds shortest distances from src
// to all other vertices using Bellman-Ford algorithm. The
// function also detects negative weight cycle
void BellmanFord(struct Graph* graph, int src)
{
int V = graph->V;
int E = graph->E;
int dist[V];
// Step 1: Initialize distances from src to all other
// vertices as INFINITE
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times. A simple
// shortest path from src to any other vertex can have
// at-most |V| - 1 edges
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX
&& dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles. The above
// step guarantees shortest distances if graph doesn't
// contain negative weight cycle. If we get a shorter
// path, then there is a cycle.
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX
&& dist[u] + weight < dist[v]) {
printf("Graph contains negative weight cycle");
return; // If negative cycle is detected, simply
// return
}
}
printArr(dist, V);
return;
}
// Driver's code
int main()
{
/* Let us create the graph given in above example */
int V = 5; // Number of vertices in graph
int E = 8; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1 (or A-B in above figure)
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
// add edge 1-4 (or B-E in above figure)
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
// Function call
BellmanFord(graph, 0);
return 0;
}
// A Java program for Bellman-Ford's single source shortest
// path algorithm.
import java.io.*;
import java.lang.*;
import java.util.*;
// A class to represent a connected, directed and weighted
// graph
class Graph {
// A class to represent a weighted edge in graph
class Edge {
int src, dest, weight;
Edge() { src = dest = weight = 0; }
};
int V, E;
Edge edge[];
// Creates a graph with V vertices and E edges
Graph(int v, int e)
{
V = v;
E = e;
edge = new Edge[e];
for (int i = 0; i < e; ++i)
edge[i] = new Edge();
}
// The main function that finds shortest distances from
// src to all other vertices using Bellman-Ford
// algorithm. The function also detects negative weight
// cycle
void BellmanFord(Graph graph, int src)
{
int V = graph.V, E = graph.E;
int dist[] = new int[V];
// Step 1: Initialize distances from src to all
// other vertices as INFINITE
for (int i = 0; i < V; ++i)
dist[i] = Integer.MAX_VALUE;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times. A simple
// shortest path from src to any other vertex can
// have at-most |V| - 1 edges
for (int i = 1; i < V; ++i) {
for (int j = 0; j < E; ++j) {
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != Integer.MAX_VALUE
&& dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles. The
// above step guarantees shortest distances if graph
// doesn't contain negative weight cycle. If we get
// a shorter path, then there is a cycle.
for (int j = 0; j < E; ++j) {
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != Integer.MAX_VALUE
&& dist[u] + weight < dist[v]) {
System.out.println(
"Graph contains negative weight cycle");
return;
}
}
printArr(dist, V);
}
// A utility function used to print the solution
void printArr(int dist[], int V)
{
System.out.println("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
System.out.println(i + "\t\t" + dist[i]);
}
// Driver's code
public static void main(String[] args)
{
int V = 5; // Number of vertices in graph
int E = 8; // Number of edges in graph
Graph graph = new Graph(V, E);
// add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// add edge 1-4 (or B-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
// Function call
graph.BellmanFord(graph, 0);
}
}
// Contributed by Aakash Hasija
# Python3 program for Bellman-Ford's single source
# shortest path algorithm.
# Class to represent a graph
class Graph:
def __init__(self, vertices):
self.V = vertices # No. of vertices
self.graph = []
# function to add an edge to graph
def addEdge(self, u, v, w):
self.graph.append([u, v, w])
# utility function used to print the solution
def printArr(self, dist):
print("Vertex Distance from Source")
for i in range(self.V):
print("{0}\t\t{1}".format(i, dist[i]))
# The main function that finds shortest distances from src to
# all other vertices using Bellman-Ford algorithm. The function
# also detects negative weight cycle
def BellmanFord(self, src):
# Step 1: Initialize distances from src to all other vertices
# as INFINITE
dist = [float("Inf")] * self.V
dist[src] = 0
# Step 2: Relax all edges |V| - 1 times. A simple shortest
# path from src to any other vertex can have at-most |V| - 1
# edges
for _ in range(self.V - 1):
# Update dist value and parent index of the adjacent vertices of
# the picked vertex. Consider only those vertices which are still in
# queue
for u, v, w in self.graph:
if dist[u] != float("Inf") and dist[u] + w < dist[v]:
dist[v] = dist[u] + w
# Step 3: check for negative-weight cycles. The above step
# guarantees shortest distances if graph doesn't contain
# negative weight cycle. If we get a shorter path, then there
# is a cycle.
for u, v, w in self.graph:
if dist[u] != float("Inf") and dist[u] + w < dist[v]:
print("Graph contains negative weight cycle")
return
# print all distance
self.printArr(dist)
# Driver's code
if __name__ == '__main__':
g = Graph(5)
g.addEdge(0, 1, -1)
g.addEdge(0, 2, 4)
g.addEdge(1, 2, 3)
g.addEdge(1, 3, 2)
g.addEdge(1, 4, 2)
g.addEdge(3, 2, 5)
g.addEdge(3, 1, 1)
g.addEdge(4, 3, -3)
# function call
g.BellmanFord(0)
# Initially, Contributed by Neelam Yadav
# Later On, Edited by Himanshu Garg
// C# program for Bellman-Ford's single source shortest
// path algorithm.
using System;
// A class to represent a connected, directed and weighted
// graph
class Graph {
// A class to represent a weighted edge in graph
class Edge {
public int src, dest, weight;
public Edge() { src = dest = weight = 0; }
};
int V, E;
Edge[] edge;
// Creates a graph with V vertices and E edges
Graph(int v, int e)
{
V = v;
E = e;
edge = new Edge[e];
for (int i = 0; i < e; ++i)
edge[i] = new Edge();
}
// The main function that finds shortest distances from
// src to all other vertices using Bellman-Ford
// algorithm. The function also detects negative weight
// cycle
void BellmanFord(Graph graph, int src)
{
int V = graph.V, E = graph.E;
int[] dist = new int[V];
// Step 1: Initialize distances from src to all
// other vertices as INFINITE
for (int i = 0; i < V; ++i)
dist[i] = int.MaxValue;
dist[src] = 0;
// Step 2: Relax all edges |V| - 1 times. A simple
// shortest path from src to any other vertex can
// have at-most |V| - 1 edges
for (int i = 1; i < V; ++i) {
for (int j = 0; j < E; ++j) {
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != int.MaxValue
&& dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// Step 3: check for negative-weight cycles. The
// above step guarantees shortest distances if graph
// doesn't contain negative weight cycle. If we get
// a shorter path, then there is a cycle.
for (int j = 0; j < E; ++j) {
int u = graph.edge[j].src;
int v = graph.edge[j].dest;
int weight = graph.edge[j].weight;
if (dist[u] != int.MaxValue
&& dist[u] + weight < dist[v]) {
Console.WriteLine(
"Graph contains negative weight cycle");
return;
}
}
printArr(dist, V);
}
// A utility function used to print the solution
void printArr(int[] dist, int V)
{
Console.WriteLine("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
Console.WriteLine(i + "\t\t" + dist[i]);
}
// Driver's code
public static void Main()
{
int V = 5; // Number of vertices in graph
int E = 8; // Number of edges in graph
Graph graph = new Graph(V, E);
// add edge 0-1 (or A-B in above figure)
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = -1;
// add edge 0-2 (or A-C in above figure)
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 4;
// add edge 1-2 (or B-C in above figure)
graph.edge[2].src = 1;
graph.edge[2].dest = 2;
graph.edge[2].weight = 3;
// add edge 1-3 (or B-D in above figure)
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 2;
// add edge 1-4 (or B-E in above figure)
graph.edge[4].src = 1;
graph.edge[4].dest = 4;
graph.edge[4].weight = 2;
// add edge 3-2 (or D-C in above figure)
graph.edge[5].src = 3;
graph.edge[5].dest = 2;
graph.edge[5].weight = 5;
// add edge 3-1 (or D-B in above figure)
graph.edge[6].src = 3;
graph.edge[6].dest = 1;
graph.edge[6].weight = 1;
// add edge 4-3 (or E-D in above figure)
graph.edge[7].src = 4;
graph.edge[7].dest = 3;
graph.edge[7].weight = -3;
// Function call
graph.BellmanFord(graph, 0);
}
// This code is contributed by Ryuga
}
// a structure to represent a connected, directed and
// weighted graph
class Edge {
constructor(src, dest, weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
}
class Graph {
constructor(V, E) {
this.V = V;
this.E = E;
this.edge = [];
}
}
function createGraph(V, E) {
const graph = new Graph(V, E);
for (let i = 0; i < E; i++) {
graph.edge[i] = new Edge();
}
return graph;
}
function printArr(dist, V) {
console.log("Vertex Distance from Source");
for (let i = 0; i < V; i++) {
console.log(`${i} \t\t ${dist[i]}`);
}
}
function BellmanFord(graph, src) {
const V = graph.V;
const E = graph.E;
const dist = [];
for (let i = 0; i < V; i++) {
dist[i] = Number.MAX_SAFE_INTEGER;
}
dist[src] = 0;
for (let i = 1; i <= V - 1; i++) {
for (let j = 0; j < E; j++) {
const u = graph.edge[j].src;
const v = graph.edge[j].dest;
const weight = graph.edge[j].weight;
if (dist[u] !== Number.MAX_SAFE_INTEGER && dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
}
}
}
for (let i = 0; i < E; i++) {
const u = graph.edge[i].src;
const v = graph.edge[i].dest;
const weight = graph.edge[i].weight;
if (dist[u] !== Number.MAX_SAFE_INTEGER && dist[u] + weight < dist[v]) {
console.log("Graph contains negative weight cycle");
return;
}
}
printArr(dist, V);
}
// Driver program to test methods of graph class
// Create a graph given in the above diagram
const V = 5;
const E = 8;
const graph = createGraph(V, E);
graph.edge[0] = new Edge(0, 1, -1);
graph.edge[1] = new Edge(0, 2, 4);
graph.edge[2] = new Edge(1, 2, 3);
graph.edge[3] = new Edge(1, 3, 2);
graph.edge[4] = new Edge(1, 4, 2);
graph.edge[5] = new Edge(3, 2, 5);
graph.edge[6] = new Edge(3, 1, 1);
graph.edge[7] = new Edge(4, 3, -3);
BellmanFord(graph, 0);
输出
顶点与源的距离 0 0 1 -1 2 2 3 -2 4 1
Bellman-Ford算法的复杂度分析:
- 图连通时的时间复杂度:
- 最佳情况: O(E),当第一次和第二次松弛后的距离数组相同时,我们可以简单地停止进一步处理
- 平均情况: O(V*E)
- 最坏情况: O(V*E)
- 图断开连接时的时间复杂度:
- 所有情况: O(E*(V^2))
- 辅助空间: O(V),其中V是图中的顶点数。
Bellman Ford 算法的应用:
- 网络路由: Bellman-Ford 用于计算机网络中查找路由表内的最短路径,帮助数据包在网络中高效导航。
- GPS 导航:GPS 设备使用 Bellman-Ford 计算位置之间最短或最快路线,从而辅助导航应用程序和设备。
- 运输和物流: Bellman-Ford算法可用于确定运输和物流中车辆的最佳路径,从而最大限度地减少燃料消耗和行程时间。
- 游戏开发: Bellman-Ford 可用于在游戏开发中为虚拟世界中的移动和导航建模,其中不同的路径可能具有不同的成本或障碍。
- 机器人和自动驾驶汽车:该算法可帮助机器人或自动驾驶汽车进行路径规划,同时考虑障碍物、地形和能源消耗。
Bellman Ford 算法的缺点:
- Bellman-Ford algorithm will fail if the graph contains any negative edge cycle.
Related articles on single source shortest path algorithms:
- Dijkstra’s Algorithm
- Floyd-Warshall Algorithm