正在载入交互式动画窗口请稍等

顺序表-数组 可视化交互式动画版

图码-数据结构可视化动画版

在这篇文章中，我们将讨论数据结构中的数组。 数组被定义为存储在连续内存位置的相似类型数据项的集合。 它是最简单的数据结构之一，其中每个数据元素可以通过使用其索引号来随机访问。

在C编程中，它们是可以存储原始类型数据的派生数据类型，例如int、char、double、float等。例如，如果我们要存储一个学生在6个科目上的成绩，那么我们不不需要为不同科目的分数定义不同的变量。 相反，我们可以定义一个数组，将每个主题的标记存储在连续的内存位置。

数组的属性

数组的一些属性如下所示 -

  • 数组中的每个元素都具有相同的数据类型，并且具有相同的大小（4 字节）。
  • 数组中的元素存储在连续的内存位置，其中第一个元素存储在最小的内存位置。
  • 数组的元素可以随机访问，因为我们可以使用给定的基地址和数据元素的大小计算数组中每个元素的地址。

数组的表示

我们可以用不同的编程语言以多种方式表示数组。 作为说明，让我们看一下 C 语言中数组的声明 -

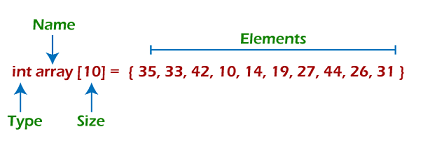
DS 中的数组

根据上图，有以下一些要点 -

  • 索引从0开始。
  • 数组的长度是10，这意味着我们可以存储10个元素。
  • 数组中的每个元素都可以通过其索引进行访问。

为什么需要数组？

数组很有用，因为 -

  • 对数组中的值进行排序和搜索更加容易。
  • 数组最适合快速轻松地处理多个值。
  • 数组适合在单个变量中存储多个值 - 在计算机编程中，大多数情况需要存储大量相似类型的数据。 为了存储如此大量的数据，我们需要定义大量的变量。 在编写程序时记住所有变量的名称是非常困难的。 与其用不同的名称命名所有变量，不如定义一个数组并将所有元素存储到其中。

数组的内存分配

如上所述，数组的所有数据元素都存储在主存储器中的连续位置。 数组的名称代表基址或主存中第一个元素的地址。 数组的每个元素都由适当的索引表示。

我们可以通过以下方式定义数组的索引 -

  1. 0（从零开始索引）：数组的第一个元素将为 arr[0]。
  2. 1（基于一的索引）：数组的第一个元素为 arr[1]。
  3. n（基于 n 的索引）：数组的第一个元素可以驻留在任意随机索引号处。
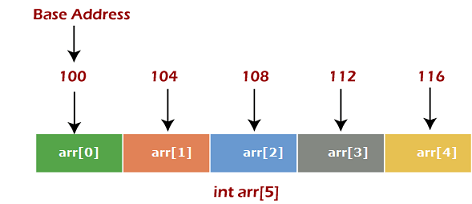
DS 中的数组

在上图中，我们显示了大小为 5 的数组 arr 的内存分配。该数组遵循从 0 开始的索引方法。 数组的基地址是100字节。 它是arr[0]的地址。 这里，使用的数据类型的大小为4字节； 因此，每个元素将在内存中占用 4 个字节。

如何访问数组中的元素？

我们需要下面给出的信息来访问数组中的任何随机元素 -

  • 数组的基地址。
  • 元素的大小（以字节为单位）。
  • 索引类型，后面是数组。

计算访问数组元素的地址的公式 -

  1. 元素 A[i] 的字节地址 = 基地址 + 大小 * ( i - 第一个索引)     

这里，size代表原始数据类型占用的内存。 例如， C 语言中 int 占用 2 个字节， float占用 4 个字节的内存空间。

我们可以通过一个例子来理解它——

假设一个数组 A[-10 ..... +2 ] 的基地址 (BA) = 999，元素大小 = 2 字节，找到 A[-1] 的位置。

L(A[-1]) = 999 + 2 x [(-1) - (-10)]

= 999 + 18

= 1017

基本操作

现在，让我们讨论数组中支持的基本操作 -

  • 遍历 - 此操作用于打印数组的元素。
  • 插入 - 用于在特定索引处添加元素。
  • 删除 - 用于从特定索引中删除元素。
  • 搜索 - 用于使用给定索引或值搜索元素。
  • 更新 - 它更新特定索引处的元素。

遍历操作

执行此操作是为了遍历数组元素。 它依次打印所有数组元素。 我们可以通过下面的程序来理解它——

  1. #include <stdio.h>   
  2. 无效  主（）{  
  3.     int  Arr[5] = {18, 30, 15, 70, 12};  
  4. 整数  我；  
  5.    printf( "数组的元素是：\n" );  
  6.     for (i = 0; i<5; i++) {  
  7.       printf( "Arr[%d] = %d," , i, Arr[i]);  
  8.    }  
  9. }  

输出

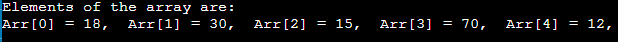
DS 中的数组

插入操作

执行此操作是为了将一个或多个元素插入到数组中。 根据要求，可以在数组的开头、结尾或任何索引处添加元素。 现在，让我们看看向数组中插入元素的实现。

  1. #include <stdio.h>   
  2. int  main()  
  3. {  
  4.      int  arr[20] = { 18, 30, 15, 70, 12 };  
  5.      int  i, x, pos, n = 5;  
  6.     printf( "插入之前的数组元素\n" );  
  7.      对于  (i = 0; i < n; i++)  
  8.         printf( "%d" , arr[i]);  
  9.     printf( “\n” );  
  10.   
  11.     x = 50；  //要插入的元素   
  12.     位置=4；  
  13.     n++；  
  14.   
  15.      对于  (i = n-1; i >= pos; i--)  
  16.         arr[i] = arr[i - 1];  
  17.     arr[位置 - 1] = x;  
  18.     printf( "插入后的数组元素\n" );  
  19.      对于  (i = 0; i < n; i++)  
  20.         printf( "%d" , arr[i]);  
  21.     printf( “\n” );  
  22.      返回  0；  
  23. }  

输出

DS 中的数组

删除操作

顾名思义，此操作从数组中删除一个元素，然后重新组织所有数组元素。

  1. #include <stdio.h>   
  2.   
  3. 无效  主（）{  
  4.     int  arr[] = {18, 30, 15, 70, 12};  
  5.     整数  k = 30，n = 5；  
  6.     整数  i，j；  
  7.      
  8.    printf( "给定的数组元素是：\n" );  
  9.       
  10.     for (i = 0; i<n; i++) {  
  11.       printf( "arr[%d] = %d," , i, arr[i]);  
  12.    }  
  13.       
  14.    j = k；  
  15.       
  16.     而 （j<n）{  
  17.       arr[j-1] = arr[j];  
  18.       j = j + 1；  
  19.    }  
  20.       
  21.    n = n -1;  
  22.      
  23.    printf( "\n删除后数组元素：\n" );  
  24.       
  25.     for (i = 0; i<n; i++) {  
  26.       printf( "arr[%d] = %d," , i, arr[i]);  
  27.    }  
  28. }  

输出

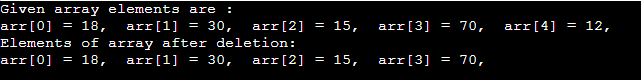
DS 中的数组

搜索操作

执行此操作是为了根据值或索引搜索数组中的元素。

  1. #include <stdio.h>   
  2.   
  3. 无效  主（）{  
  4.     int  arr[5] = {18, 30, 15, 70, 12};  
  5.     int  item = 70, i, j=0 ;  
  6.      
  7.    printf( "给定的数组元素是：\n" );  
  8.       
  9.     for (i = 0; i<5; i++) {  
  10.       printf( "arr[%d] = %d," , i, arr[i]);  
  11.    }  
  12.     printf( "\n要搜索的元素 = %d" , item);  
  13.     而 （ j < 5）{  
  14.        if ( arr[j] == 项目 ) {  
  15.           打破 ；  
  16.       }  
  17.           
  18.       j = j + 1；  
  19.    }  
  20.       
  21.    printf( "\n元素 %d 在 %d 位置找到" , item, j+1);  
  22. }  

输出

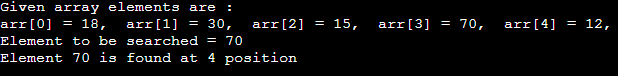
DS 中的数组

更新操作

执行此操作是为了更新位于给定索引处的现有数组元素。

  1. #include <stdio.h>   
  2.   
  3. 无效  主（）{  
  4.     int  arr[5] = {18, 30, 15, 70, 12};  
  5.     int  item = 50，i，pos = 3；  
  6.      
  7.    printf( "给定的数组元素是：\n" );  
  8.       
  9.     for (i = 0; i<5; i++) {  
  10.       printf( "arr[%d] = %d," , i, arr[i]);  
  11.    }  
  12.       
  13. arr[pos-1] = 项目；    
  14.    printf( "\n更新后的数组元素:\n" );  
  15.       
  16.     for (i = 0; i<5; i++) {  
  17.       printf( "arr[%d] = %d," , i, arr[i]);  
  18.    }  
  19. }  

输出

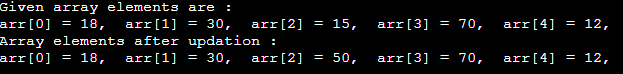
DS 中的数组

数组操作的复杂性

下表描述了各种数组操作的时间和空间复杂度。

时间复杂度

手术 平均情况 最坏的情况下
使用权 复杂度(1) 复杂度(1)
搜索 在） 在）
插入 在） 在）
删除 在） 在）

空间复杂度

在数组中，最坏情况的空间复杂度为 O(n) 。

数组的优点

  • 数组为同一类型的变量组提供单一名称。 因此，很容易记住数组所有元素的名称。
  • 遍历数组是一个非常简单的过程； 我们只需要增加数组的基地址就可以一一访问每个元素。
  • 数组中的任何元素都可以通过索引直接访问。

数组的缺点

  • 数组是同质的。 这意味着可以在其中存储具有相似数据类型的元素。
  • 在数组中，存在静态内存分配，即数组的大小无法更改。
  • 如果我们存储的元素数量少于声明的大小，就会浪费内存。

结论

在本文中，我们讨论了特殊的数据结构，即数组，以及对其执行的基本操作。 数组提供了一种独特的方式来构造存储的数据，以便可以轻松访问并使用索引进行查询以获取值。

二维数组可以定义为数组的数组。 二维数组被组织为矩阵，可以表示为行和列的集合。

然而，创建二维数组是为了实现类似于关系数据库的数据结构。 它可以轻松地一次保存大量数据，这些数据可以在需要时传递到任意数量的函数。

如何声明二维数组

声明二维数组的语法与一维数组的语法非常相似，如下所示。

  1. int  arr[最大行数][最大列数];   

但是，它生成的数据结构如下所示。


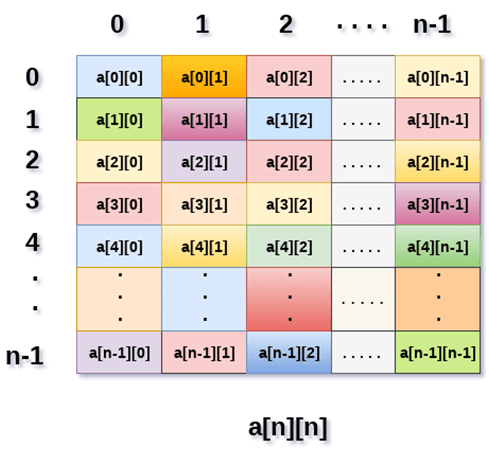
DS 二维阵列

上图显示了二维数组，元素以行和列的形式组织。 第一行的第一个元素由 a[0][0] 表示，其中第一个索引中显示的数字是该行的编号，而第二个索引中显示的数字是列的编号。

我们如何访问二维数组中的数据

由于二维数组的元素可以随机访问。 与一维数组类似，我们可以使用单元格的索引来访问二维数组中的各个单元格。 特定单元格有两个索引，一个是其行号，另一个是其列号。

但是，我们可以使用以下语法将存储在 2D 数组的任何特定单元格中的值存储到某个变量 x 中。

  1. int  x = a[i][j];   

其中 i 和 j 分别是单元格的行号和列号。

我们可以使用以下代码将 2D 数组的每个单元格分配为 0：

  1. for  (  int  i= 0 ; i<n ;i++)  
  2. {  
  3.      for  ( int  j= 0 ; j<n; j++)   
  4.     {  
  5.         a[i][j] =  0 ；   
  6.     }  
  7. }  

初始化二维数组

我们知道，在C编程中同时声明和初始化一维数组时，不需要指定数组的大小。 然而，这不适用于二维数组。 我们必须至少定义数组的第二个维度。

声明和初始化二维数组的语法如下。

  1. int  arr[ 2 ][ 2 ] = { 0 , 1 , 2 , 3 };   

二维数组中可以存在的元素数量始终等于（ 行数 * 列数 ）。

示例： 将用户数据存储到二维数组中并打印。

C 示例：

  1. #include <stdio.h>  
  2. 无效  主()  
  3. {  
  4.      int  arr[ 3 ][ 3 ],i,j;   
  5.      对于  (i= 0 ;i< 3 ;i++)  
  6.     {  
  7.          对于  (j= 0 ;j< 3 ;j++)  
  8.         {  
  9.             printf( "输入a[%d][%d]:" ,i,j);              
  10.             scanf( "%d" ,&arr[i][j]);  
  11.         }  
  12.     }  
  13.     printf( "\n 打印元素 ....\n" );   
  14.      对于 (i= 0 ;i< 3 ;i++)  
  15.     {  
  16.         printf( “\n” );  
  17.          对于  (j= 0 ;j< 3 ;j++)  
  18.         {  
  19.             printf( "%d\t" ,arr[i][j]);  
  20.         }  
  21.     }  
  22. }  

Java示例

  1. 导入  java.util.Scanner；  
  2. 公共类 TwoDArray {  
  3. publicstaticvoid main(String[] args) {  
  4.      int [][] arr = newint[ 3 ][ 3 ];  
  5.     扫描仪 sc =  新  扫描仪(System.in);  
  6.      对于  (inti = 0 ;i< 3 ;i++)  
  7.     {  
  8.          对于 (intj= 0 ;j< 3 ;j++)  
  9.         {  
  10.             System.out.print( "输入元素" );  
  11.             arr[i][j]=sc.nextInt();  
  12.             System.out.println();  
  13.         }  
  14.     }  
  15.     System.out.println( "打印元素..." );  
  16.      对于 (inti= 0 ;i< 3 ;i++)  
  17.     {   
  18.         System.out.println();  
  19.          对于 (intj= 0 ;j< 3 ;j++)  
  20.         {  
  21.             System.out.print(arr[i][j]+ "\t" );  
  22.         }  
  23.     }  
  24. }  
  25. }  

C# 示例

  1. 使用系统；  
  2.                       
  3. 公开 课  节目    
  4. {  
  5.      公共 静态 无效  Main（）      
  6.     {  
  7.          int [,] arr =  新 int [ 3 , 3 ];    
  8.          for  ( int  i= 0 ;i< 3 ;i++)  
  9.         {  
  10.              for  ( int  j= 0 ;j< 3 ;j++)  
  11.             {  
  12.                 Console.WriteLine( "输入元素" );  
  13.                 arr[i,j]= Convert.ToInt32(Console.ReadLine());  
  14.             }  
  15.         }  
  16.         Console.WriteLine( "正在打印元素..." );  
  17.          for  ( int  i= 0 ;i< 3 ;i++)  
  18.         {  
  19.             Console.WriteLine();  
  20.              for  ( int  j= 0 ;j< 3 ;j++)  
  21.             {  
  22.                 Console.Write(arr[i,j]+ " " );  
  23.             }  
  24.         }  
  25.     }  
  26. }  

将 2D 数组映射到 1D 数组

当谈到映射二维数组时，我们大多数人可能会想到为什么需要这种映射。 然而，从用户的角度来看，二维数组是存在的。 创建二维数组是为了实现类似关系数据库表的数据结构，在计算机内存中，二维数组的存储技术类似于一维数组。

二维数组的大小等于数组中的行数和列数的乘积。 我们确实需要将二维数组映射到一维数组，以便将它们存储在内存中。

下图显示了 3 X 3 二维数组。 然而，这个数组需要映射到一维数组才能将其存储到内存中。


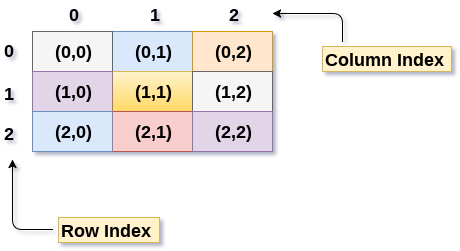
DS 二维阵列

将二维数组元素存储到内存中的主要技术有两种

1.行主排序

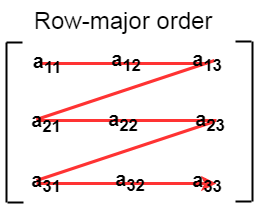
在行主排序中，二维数组的所有行都连续存储到内存中。 考虑到上图中显示的数组，其根据行主顺序的内存分配如下所示。


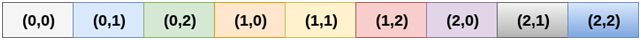
DS 二维阵列

首先，将 数组的第一行完全存储到内存中，然后将数组的第二 行 完全存储到内存中，依此类推，直到最后一行 。


DS 二维阵列

2. 栏目主要排序

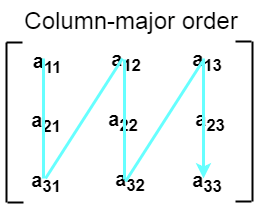
根据列主排序，二维数组的所有列都连续存储到内存中。 上图中所示数组的内存分配如下。


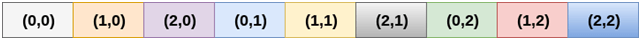
DS 二维阵列

首先，将数组的第一 列 完全存储到内存中，然后将 数组的第二行完全存储到内存中，依此类推，直到数组的最后一列 。


DS 二维阵列

计算二维数组的随机元素的地址

由于存在两种不同的将二维数组存储到内存中的技术，因此有两种不同的公式来计算二维数组的随机元素的地址。

按行主要顺序

如果数组由 a[m][n] 声明，其中 m 是行数，n 是列数，则按行主序存储的数组元素 a[i][j] 的地址计算如下,

  1. 地址(a[i][j]) = B.A. + (i * n + j) * 大小   

其中， BA 是基地址或数组 a[0][0] 的第一个元素的地址。

例子 ：

  1. a[ 10 ... 30 ,  55 ... 75 ]，数组基地址 (BA) =  0 ，元素大小 =  4 个  字节。   
  2. 找到a[ 15 ][ 68 ]的位置 。   
  3.   
  4. 地址(a[ 15 ][ 68 ]) =  0  +   
  5. (( 15-10 )  ×  ( 68-55 +  1  ) + ( 68-55 ) )   ×   4    
  6.   
  7. = ( 5  x  14  +  13 ) x  4   
  8. =  83  x  4    
  9. =  332 个  答案   

按栏目主要顺序

如果数组由 a[m][n] 声明，其中 m 是行数，n 是列数，则按行主序存储的数组元素 a[i][j] 的地址计算如下,

  1. 地址(a[i][j]) = ((j*m)+i)*大小 + BA   

其中 BA 是数组的基地址。

例子：

  1. A [- 5  ... + 20 ][ 20  ...  70 ]，BA =  1020 ，元素大小 =  8  字节。 找到a[ 0 ][ 30 ] 的位置 。   
  2.   
  3. 地址 [A[ 0 ][ 30 ]) = (( 30 - 20 ) x  24  +  5 ) x  8  +  1020    =   245  x  8  +  1020  =  2980  字节   

无论你的目标是考试成功、职业发展，还是纯粹的兴趣，这个数据结构和算法可视化的网站都会是一个无价的资源。

前往这个网站，开始你的学习之旅吧！

这些是常见的：【C语言描述】《数据结构和算法》数据结构JAVA实现 数据结构与算法基础（青岛大学-王卓）数据结构与算法王道数据结构c语言实现 速成数据结构期末考前救急 数据结构视频C语言版教程 数据结构严蔚敏 数据结构郝斌 数据结构考研 JAVA数据结构算法与基础 数据结构王道 2022数据结构学习 数据结构小甲鱼 王卓 学习数据结构 数据结构浙江大学 数据结构复习 数据结构马士兵 数据结构零基础教程 数据结构和算法 数据结构入门 考研数据结构习题讲解 数据结构期末复习 计算机二级