Prim(普里姆)算法可视化交互式动画版

Prim的算法简介：

我们已经讨论了最小生成树的 Kruskal 算法。与Kruskal算法一样，Prim算法也是一种贪心算法。该算法始终从单个节点开始，然后移动到多个相邻节点，以便探索沿途所有连接的边。

该算法从空的生成树开始。这个想法是维护两组顶点。第一个集合包含已包含在 MST 中的顶点，另一个集合包含尚未包含在 MST 中的顶点。在每一步中，它都会考虑连接两个集合的所有边，并从这些边中选择最小权重边。拾取边后，它将边的另一个端点移动到包含 MST 的集合。

连接图中两组顶点的一组边在图论中称为割。因此，在 Prim 算法的每一步中，找到一个切割，从切割中选取最小权重边，并将该顶点包含在 MST 集合（包含已包含顶点的集合）中。

Prim 算法如何工作？

Prim 算法的工作原理可以通过以下步骤来描述：

步骤1： 确定任意一个顶点作为MST的起始顶点。
步骤2： 按照步骤3到5，直到出现未包含在MST中的顶点（称为边缘顶点）。
步骤3： 找到连接任意树顶点和边缘顶点的边。
第四步： 找到这些边中的最小值。
步骤5： 如果选择的边不形成任何环，则将其添加到MST中。
步骤6： 返回MST并退出

注意： 为了确定环，我们可以将顶点分为两组[一组包含MST中包含的顶点，另一组包含边缘顶点。]

Prim算法说明：

以下图为例，我们需要找到最小生成树（MST）。

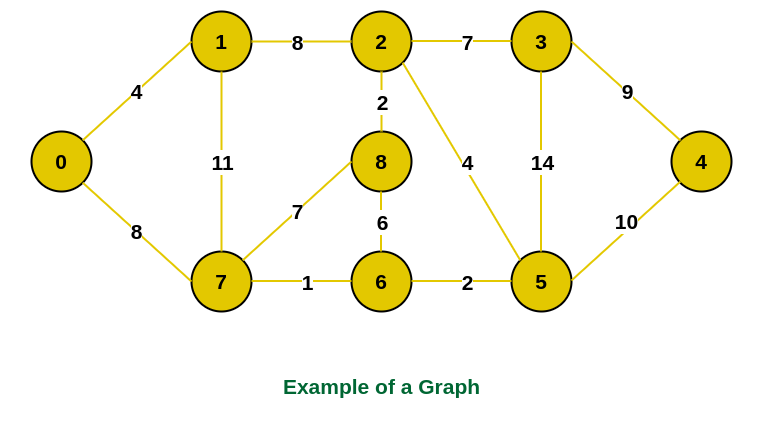
图表示例

步骤1： 首先，我们选择一个任意顶点作为最小生成树的起始顶点。这里我们选择顶点 0 作为起始顶点。

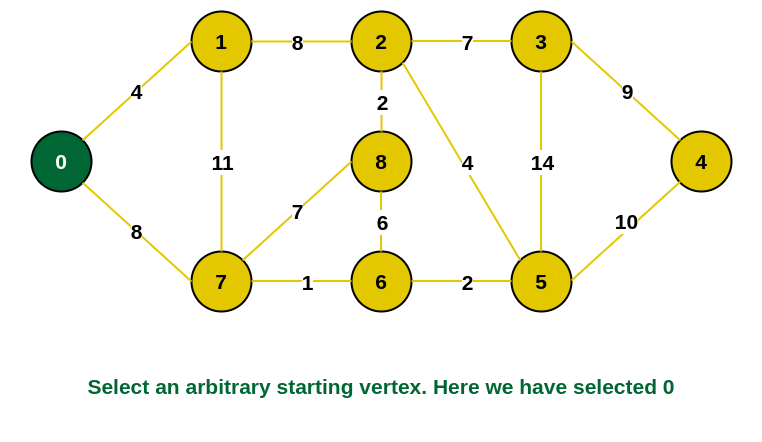
选择 0 作为起始顶点

步骤2： 连接不完整MST和其他顶点的所有边都是边{0, 1}和{0, 7}。在这两者之间，权重最小的边是{0, 1}。因此，将边和顶点 1 包含在 MST 中。

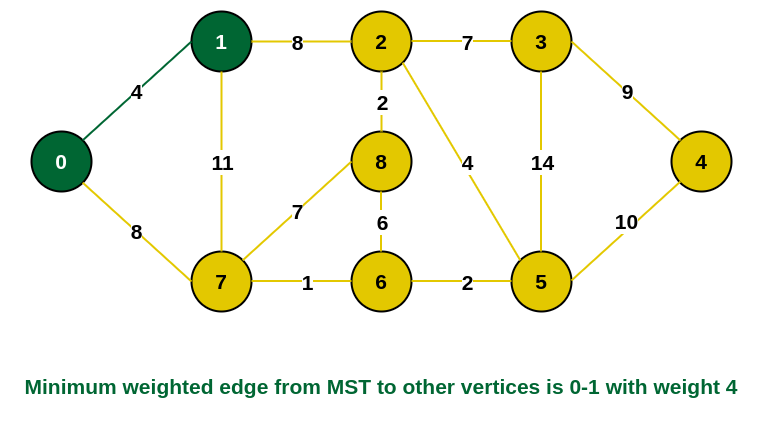
MST中添加1

步骤3： 连接不完整MST到其他顶点的边是{0, 7}、{1, 7}和{1, 2}。在这些边中，边{0, 7}和{1, 2}的最小权重为8。让我们在 MST 中包含边 {0, 7} 和顶点 7。 [我们还可以在 MST 中包含边 {1, 2} 和顶点 2]。

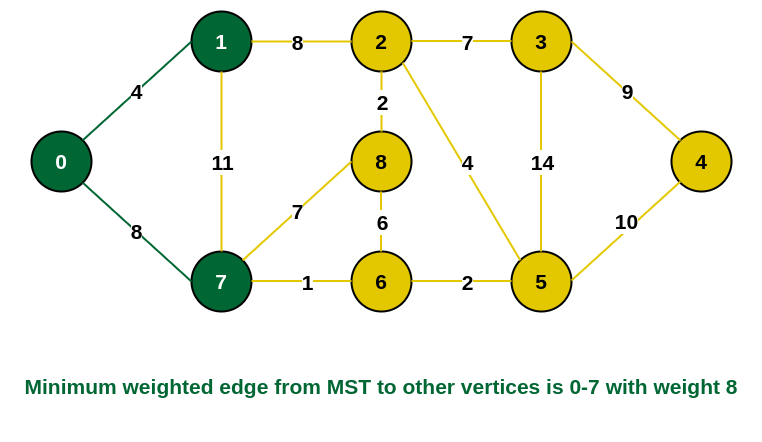
MST中添加7

步骤4： 连接不完整MST与边缘顶点的边为{1, 2}、{7, 6}和{7, 8}。将边 {7, 6} 和顶点 6 添加到 MST 中，因为它的权重最小（即 1）。

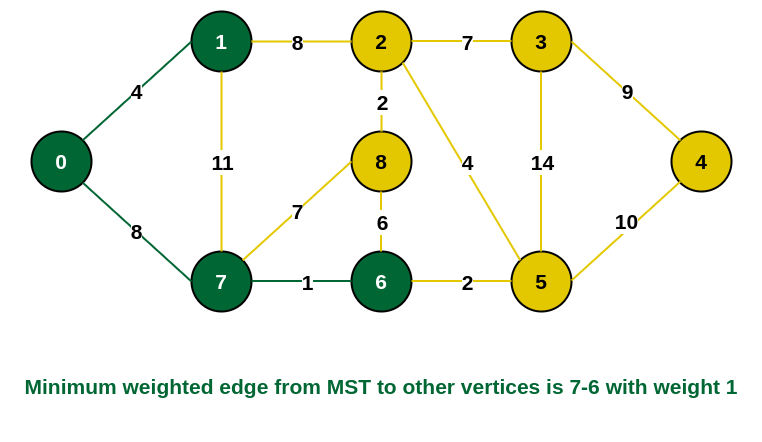
MST中添加6

第 5 步： 连接边现在为 {7, 8}、{1, 2}、{6, 8} 和 {6, 5}。将边{6, 5}和顶点5包含在MST中，因为其中边的权重最小（即2）。

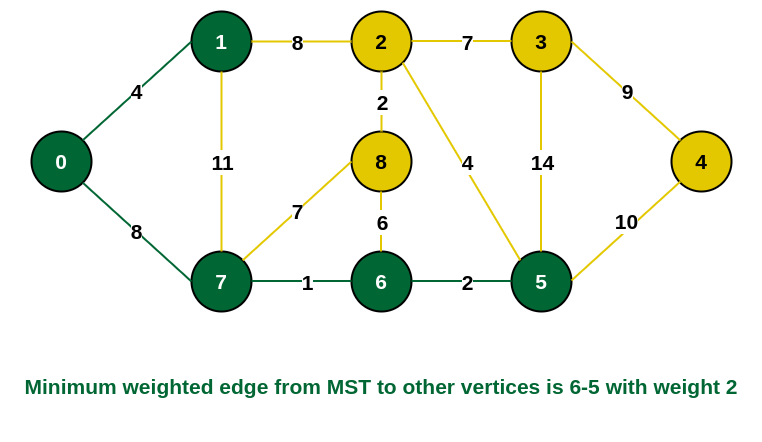
将顶点 5 包含在 MST 中

步骤6： 当前连接边中，边{5, 2}的权重最小。因此，将该边和顶点 2 包含在 MST 中。

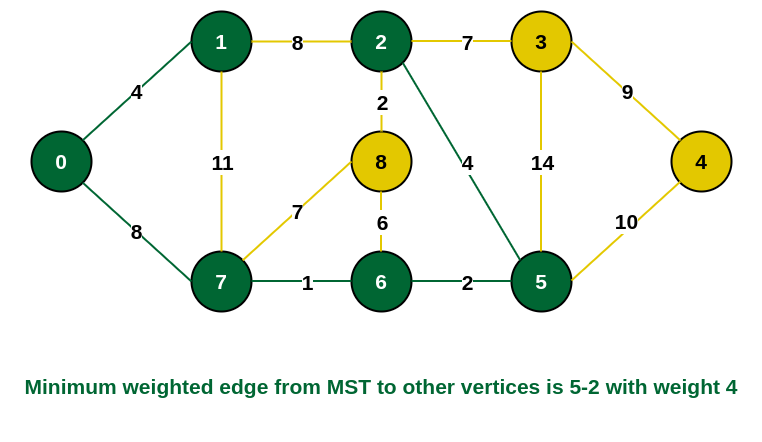
将顶点 2 包含在 MST 中

步骤7： 不完整MST与其他边的连接边为{2, 8}、{2, 3}、{5, 3}和{5, 4}。权重最小的边是边 {2, 8}，其权重为 2。因此，将该边和顶点 8 包含在 MST 中。

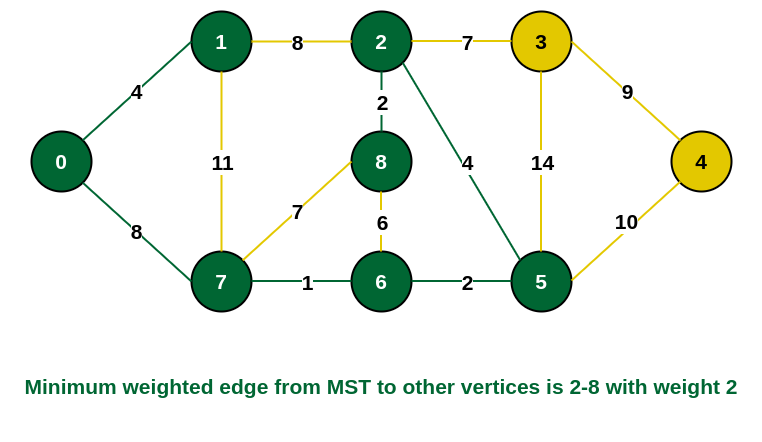
在 MST 中添加顶点 8

步骤8： 看到这里，边{7, 8}和{2, 3}都具有相同的权重，并且权重最小。但 7 已经是 MST 的一部分。因此，我们将考虑边 {2, 3} 并将该边和顶点 3 包含在 MST 中。

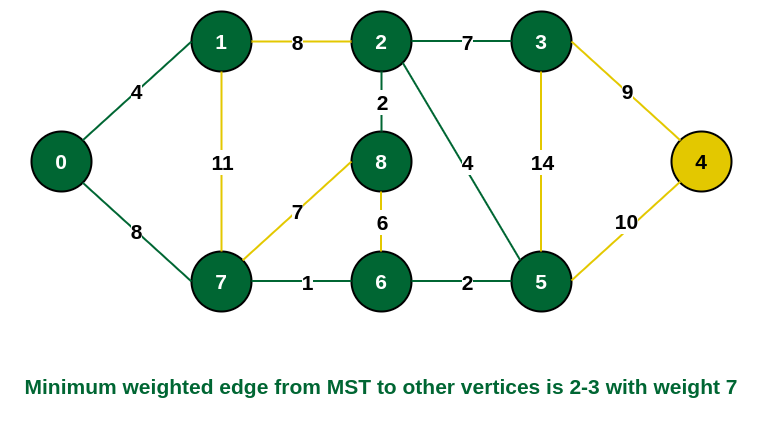
在 MST 中包含顶点 3

步骤9： 仅保留顶点4。从不完整的MST到4的最小加权边是{3, 4}。

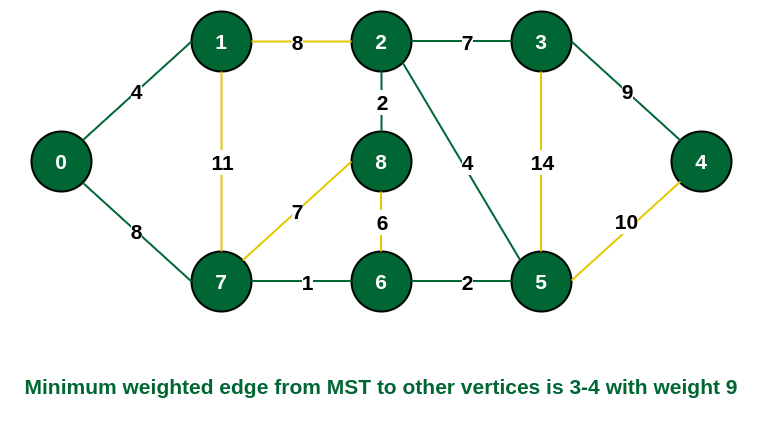
将顶点 4 包含在 MST 中

MST的最终结构如下，MST边的权重为 (4 + 8 + 1 + 2 + 4 + 2 + 7 + 9) = 37 。

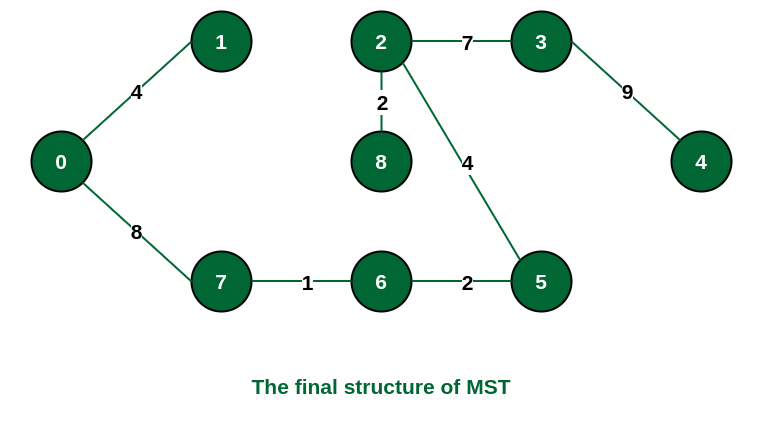
使用上述方法形成的MST的结构

注意： 如果我们在第三步中选择了边 {1, 2}，则 MST 将如下所示。

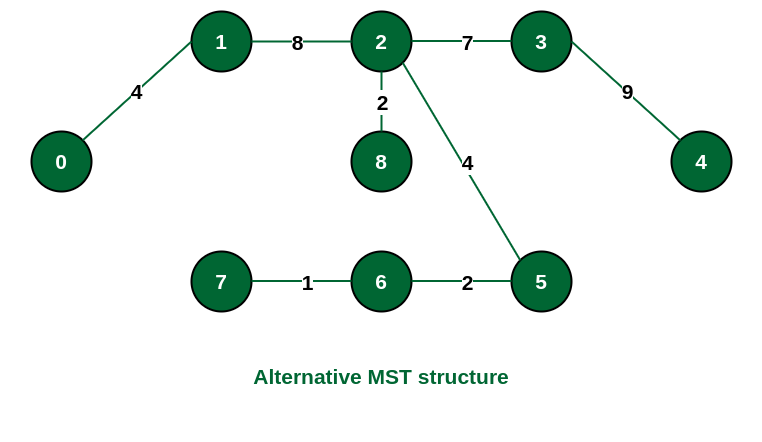
如果我们在 MST 中选择了边 {1, 2}，则备用 MST 的结构

如何实现Prim算法？

按照给定的步骤使用上面提到的 Prim 算法 来查找图的 MST：

创建一个 mstSet 集来跟踪已包含在 MST 中的顶点。
为输入图中的所有顶点分配一个键值。将所有键值初始化为 INFINITE。将第一个顶点的键值指定为 0，以便首先选取它。
虽然 mstSet 不包含所有顶点
- 选择一个不在 mstSet 中且具有最小键值的顶点 u 。
- 将u 包含在 mstSet 中。
- 更新u 所有相邻顶点的键值。要更新键值，请迭代所有相邻顶点。
  - 对于每个相邻顶点 v ，如果边 uv 的权重小于 v 的前一个键值，则将键值更新为 uv 的权重。

使用关键值的想法是从切割中选取最小权重边缘。键值仅用于尚未包含在 MST 中的顶点，这些顶点的键值表示将它们连接到 MST 中包含的顶点集的最小权重边。

下面是该方法的实现：

C++

              
                
                    // A C++ program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
 
#include <bits/stdc++.h>
using namespace std;
 
// Number of vertices in the graph
#define V 5
 
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
                        
int minKey(int key[], bool mstSet[])
{
    // Initialize min value
    int
                          min = INT_MAX, min_index;
 
    for (int v = 0; v < V; v++)
        if (mstSet[v] == false && key[v] < min)
                        
            min = key[v], min_index = v;
 
    return min_index;
}
 
// A utility function to print the
// constructed MST stored in parent[]
void printMST(int parent[], int graph[V][V])
{
    cout << "Edge \tWeight\n";
    for (int i = 1; i < V; i++)
        cout << parent[i] << " - "
                          << i << " \t"
             << graph[i][parent[i]] << " \n";
}
 
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
                        
void primMST(int graph[V][V])
{
    // Array to store constructed MST
    int
                          parent[V];
 
    // Key values used to pick minimum weight edge in cut
    int
                          key[V];
 
    // To represent set of vertices included in MST
    bool mstSet[V];
 
    // Initialize all keys as INFINITE
    for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;
 
    // Always include first 1st vertex in MST.
    // Make key 0 so that this vertex is picked as first
    // vertex.
    key[0] = 0;
   
                        
    // First node is always root of MST
    parent[0] = -1;
 
    // The MST will have V vertices
    for (int count = 0; count < V - 1; count++) {
         
        // Pick the minimum key vertex from the
        // set of vertices not yet included in MST
        int u = minKey(key, mstSet);
 
        // Add the picked vertex to the MST Set
        mstSet[u] = true;
 
        // Update key value and parent index of
        // the adjacent vertices of the picked vertex.
        // Consider only those vertices which are not
        // yet included in MST
        for (int v = 0; v < V; v++)
 
            // graph[u][v] is non zero only for adjacent
            // vertices of m mstSet[v] is false for vertices
            // not yet included in MST Update the key only
            // if graph[u][v] is smaller than key[v]
            if (graph[u][v] && mstSet[v] == false
                && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }
 
    // Print the constructed MST
    printMST(parent, graph);
}
 
// Driver's code
int main()
{
    int
                          graph[V][V] = { { 0, 2, 0, 6, 0 },
                        { 2, 0, 3, 8, 5 },
                        { 0, 3, 0, 0, 7 },
                        { 6, 8, 0, 0, 9 },
                        { 0, 5, 7, 9, 0 } };
 
    // Print the solution
    primMST(graph);
 
    return 0;
}
 
// This code is contributed by rathbhupendra

                  

              
            

C

              
                
                    // A C program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
 
#include <limits.h>
#include <stdbool.h>
#include <stdio.h>
                        
 
// Number of vertices in the graph
#define V 5
 
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
                        
int minKey(int key[], bool mstSet[])
{
    // Initialize min value
    int
                          min = INT_MAX, min_index;
 
    for (int v = 0; v < V; v++)
        if (mstSet[v] == false && key[v] < min)
                        
            min = key[v], min_index = v;
 
    return min_index;
}
 
// A utility function to print the
// constructed MST stored in parent[]
int printMST(int parent[], int graph[V][V])
{
    printf("Edge \tWeight\n");
    for (int i = 1; i < V; i++)
        printf("%d - %d \t%d \n", parent[i], i,
               graph[i][parent[i]]);
}
 
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
                        
void primMST(int graph[V][V])
{
    // Array to store constructed MST
    int
                          parent[V];
    // Key values used to pick minimum weight edge in cut
    int
                          key[V];
    // To represent set of vertices included in MST
    bool mstSet[V];
 
    // Initialize all keys as INFINITE
    for (int i = 0; i < V; i++)
        key[i] = INT_MAX, mstSet[i] = false;
 
    // Always include first 1st vertex in MST.
    // Make key 0 so that this vertex is picked as first
    // vertex.
    key[0] = 0;
   
                        
    // First node is always root of MST
    parent[0] = -1;
 
    // The MST will have V vertices
    for (int count = 0; count < V - 1; count++) {
         
        // Pick the minimum key vertex from the
        // set of vertices not yet included in MST
        int u = minKey(key, mstSet);
 
        // Add the picked vertex to the MST Set
        mstSet[u] = true;
 
        // Update key value and parent index of
        // the adjacent vertices of the picked vertex.
        // Consider only those vertices which are not
        // yet included in MST
        for (int v = 0; v < V; v++)
 
            // graph[u][v] is non zero only for adjacent
            // vertices of m mstSet[v] is false for vertices
            // not yet included in MST Update the key only
            // if graph[u][v] is smaller than key[v]
            if (graph[u][v] && mstSet[v] == false
                && graph[u][v] < key[v])
                parent[v] = u, key[v] = graph[u][v];
    }
 
    // print the constructed MST
    printMST(parent, graph);
}
 
// Driver's code
int main()
{
    int
                          graph[V][V] = { { 0, 2, 0, 6, 0 },
                        { 2, 0, 3, 8, 5 },
                        { 0, 3, 0, 0, 7 },
                        { 6, 8, 0, 0, 9 },
                        { 0, 5, 7, 9, 0 } };
 
    // Print the solution
    primMST(graph);
 
    return 0;
}

                  

              
            

Java

              
                
                    // A Java program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency matrix
// representation of the graph
 
import java.io.*;
import java.lang.*;
import java.util.*;
 
class MST {
 
    // Number of vertices in the graph
    private
                          static final int V = 5;
 
    // A utility function to find the vertex with minimum
    // key value, from the set of vertices not yet included
    // in MST
    int
                          minKey(int key[], Boolean mstSet[])
    {
        // Initialize min value
        int min = Integer.MAX_VALUE, min_index = -1;
 
        for (int
                          v = 0; v < V; v++)
            if (mstSet[v] == false && key[v] < min) {
                min = key[v];
                min_index = v;
            }
 
        return min_index;
    }
 
    // A utility function to print the constructed MST
    // stored in parent[]
    void
                          printMST(int parent[], int graph[][])
    {
        System.out.println("Edge \tWeight");
        for (int
                          i = 1; i < V; i++)
            System.out.println(parent[i] + " - " + i + "\t"
                               + graph[i][parent[i]]);
    }
 
    // Function to construct and print MST for a graph
    // represented using adjacency matrix representation
    void
                          primMST(int graph[][])
    {
        // Array to store constructed MST
        int parent[] = new int[V];
                        
 
        // Key values used to pick minimum weight edge in
        // cut
        int key[] = new int[V];
                        
 
        // To represent set of vertices included in MST
        Boolean mstSet[] = new Boolean[V];
 
        // Initialize all keys as INFINITE
        for (int
                          i = 0; i < V; i++) {
            key[i] = Integer.MAX_VALUE;
            mstSet[i] = false;
        }
 
        // Always include first 1st vertex in MST.
        // Make key 0 so that this vertex is
        // picked as first vertex
        key[0] = 0;
       
        // First node is always root of MST
        parent[0] = -1;
 
        // The MST will have V vertices
        for (int
                          count = 0; count < V - 1; count++) {
             
                        
            // Pick the minimum key vertex from the set of
            // vertices not yet included in MST
            int u = minKey(key, mstSet);
 
            // Add the picked vertex to the MST Set
            mstSet[u] = true;
 
            // Update key value and parent index of the
            // adjacent vertices of the picked vertex.
            // Consider only those vertices which are not
            // yet included in MST
            for (int
                          v = 0; v < V; v++)
 
                // graph[u][v] is non zero only for adjacent
                // vertices of m mstSet[v] is false for
                // vertices not yet included in MST Update
                // the key only if graph[u][v] is smaller
                // than key[v]
                if (graph[u][v] != 0 && mstSet[v] == false
                    && graph[u][v] < key[v]) {
                    parent[v] = u;
                    key[v] = graph[u][v];
                }
        }
 
        // Print the constructed MST
        printMST(parent, graph);
    }
 
    public
                          static void main(String[] args)
    {
        MST t = new MST();
        int graph[][] = new int[][] { { 0, 2, 0, 6, 0 },
                                      { 2, 0, 3, 8, 5 },
                                      { 0, 3, 0, 0, 7 },
                                      { 6, 8, 0, 0, 9 },
                                      { 0, 5, 7, 9, 0 } };
 
        // Print the solution
        t.primMST(graph);
    }
}
 
// This code is contributed by Aakash Hasija

                  

              
            

Python3

              
                
                    # A Python3 program for 
                        
# Prim's Minimum Spanning Tree (MST) algorithm.
# The program is for adjacency matrix 
# representation of the graph
 
# Library for INT_MAX
import sys
 
 
class Graph():
    def
                          __init__(self, vertices):
        self.V = vertices
        self.graph =
                          [[0 for
                          column in range(vertices)]
                      for row in
                          range(vertices)]
 
    # A utility function to print 
    # the constructed MST stored in parent[]
    def
                          printMST(self, parent):
        print("Edge \tWeight")
        for i in
                          range(1, self.V):
            print(parent[i], "-", i, "\t", self.graph[i][parent[i]])
 
    # A utility function to find the vertex with
    # minimum distance value, from the set of vertices
    # not yet included in shortest path tree
    def
                          minKey(self, key, mstSet):
 
        # Initialize min value
        min = sys.maxsize
 
        for v in
                          range(self.V):
            if key[v] < min and mstSet[v] ==
                          False:
                min = key[v]
                min_index = v
                        
 
        return min_index
 
    # Function to construct and print MST for a graph
    # represented using adjacency matrix representation
    def
                          primMST(self):
 
        # Key values used to pick minimum weight edge in cut
        key = [sys.maxsize] * self.V
        parent = [None] * self.V  # Array to store constructed MST
        # Make key 0 so that this vertex is picked as first vertex
        key[0] = 0
        mstSet = [False] * self.V
 
        parent[0] = -1 
                          # First node is always the root of
 
        for cout in
                          range(self.V):
 
            # Pick the minimum distance vertex from
            # the set of vertices not yet processed.
            # u is always equal to src in first iteration
            u = self.minKey(key, mstSet)
 
            # Put the minimum distance vertex in
            # the shortest path tree
            mstSet[u] = True
 
            # Update dist value of the adjacent vertices
            # of the picked vertex only if the current
            # distance is greater than new distance and
            # the vertex in not in the shortest path tree
            for v in
                          range(self.V):
 
                # graph[u][v] is non zero only for adjacent vertices of m
                # mstSet[v] is false for vertices not yet included in MST
                # Update the key only if graph[u][v] is smaller than key[v]
                if self.graph[u][v] > 0 and mstSet[v] == False
                          \
                and key[v] > self.graph[u][v]:
                    key[v] = self.graph[u][v]
                    parent[v] = u
                        
 
        self.printMST(parent)
 
 
# Driver's code
if __name__ ==
                          '__main__':
    g = Graph(5)
    g.graph = [[0, 2, 0, 6, 0],
               [2, 0, 3, 8, 5],
               [0, 3, 0, 0, 7],
               [6, 8, 0, 0, 9],
               [0, 5, 7, 9, 0]]
 
    g.primMST()
 
 
# Contributed by Divyanshu Mehta

                  

              
            

C#

              
                
                    // A C# program for Prim's Minimum
// Spanning Tree (MST) algorithm.
// The program is for adjacency
// matrix representation of the graph
 
using System;
class MST {
 
    // Number of vertices in the graph
    static
                          int V = 5;
 
    // A utility function to find
    // the vertex with minimum key
    // value, from the set of vertices
    // not yet included in MST
    static
                          int minKey(int[] key, bool[] mstSet)
    {
        // Initialize min value
        int min = int.MaxValue, min_index = -1;
 
        for (int
                          v = 0; v < V; v++)
            if (mstSet[v] == false && key[v] < min) {
                min = key[v];
                min_index = v;
            }
 
        return min_index;
    }
 
    // A utility function to print
    // the constructed MST stored in parent[]
    static
                          void printMST(int[] parent, int[, ] graph)
    {
        Console.WriteLine("Edge \tWeight");
        for (int
                          i = 1; i < V; i++)
            Console.WriteLine(parent[i] + " - " + i + "\t"
                              + graph[i, parent[i]]);
    }
 
    // Function to construct and
    // print MST for a graph represented
    // using adjacency matrix representation
    static
                          void primMST(int[, ] graph)
    {
        // Array to store constructed MST
        int[] parent = new int[V];
                        
 
        // Key values used to pick
        // minimum weight edge in cut
        int[] key = new int[V];
                        
 
        // To represent set of vertices
        // included in MST
        bool[] mstSet = new bool[V];
                        
 
        // Initialize all keys
        // as INFINITE
        for (int
                          i = 0; i < V; i++) {
            key[i] = int.MaxValue;
            mstSet[i] = false;
        }
 
        // Always include first 1st vertex in MST.
        // Make key 0 so that this vertex is
        // picked as first vertex
        // First node is always root of MST
        key[0] = 0;
        parent[0] = -1;
 
        // The MST will have V vertices
        for (int
                          count = 0; count < V - 1; count++) {
 
            // Pick the minimum key vertex
            // from the set of vertices
            // not yet included in MST
            int u = minKey(key, mstSet);
 
            // Add the picked vertex
            // to the MST Set
            mstSet[u] = true;
 
            // Update key value and parent
            // index of the adjacent vertices
            // of the picked vertex. Consider
            // only those vertices which are
            // not yet included in MST
            for (int
                          v = 0; v < V; v++)
 
                // graph[u][v] is non zero only
                // for adjacent vertices of m
                // mstSet[v] is false for vertices
                // not yet included in MST Update
                // the key only if graph[u][v] is
                // smaller than key[v]
                if (graph[u, v] != 0 && mstSet[v] == false
                    && graph[u, v] < key[v]) {
                    parent[v] = u;
                    key[v] = graph[u, v];
                }
        }
 
        // Print the constructed MST
        printMST(parent, graph);
    }
 
    // Driver's Code
    public
                          static void Main()
    {
        int[, ] graph = new int[, ] { { 0, 2, 0, 6, 0 },
                                      { 2, 0, 3, 8, 5 },
                                      { 0, 3, 0, 0, 7 },
                                      { 6, 8, 0, 0, 9 },
                                      { 0, 5, 7, 9, 0 } };
 
        // Print the solution
        primMST(graph);
    }
}
 
// This code is contributed by anuj_67.

                  

              
            

Javascript

              
                
                    <script>
 
// Number of vertices in the graph 
let V = 5;
 
// A utility function to find the vertex with 
// minimum key value, from the set of vertices 
// not yet included in MST 
                        
function minKey(key, mstSet) 
{ 
    // Initialize min value 
    let min = Number.MAX_VALUE, min_index; 
 
    for
                          (let v = 0; v < V; v++) 
        if (mstSet[v] == false && key[v] < min) 
            min = key[v], min_index = v; 
 
    return
                          min_index; 
} 
 
// A utility function to print the 
// constructed MST stored in parent[] 
function printMST(parent, graph) 
{ 
    document.write("Edge      Weight" + "<br>"); 
    for
                          (let i = 1; i < V; i++) 
        document.write(parent[i] + "   -  " + i + "     " + graph[i][parent[i]] + "<br>"); 
} 
 
// Function to construct and print MST for 
// a graph represented using adjacency 
// matrix representation 
                        
function primMST(graph) 
{ 
    // Array to store constructed MST 
    let parent = []; 
     
    // Key values used to pick minimum weight edge in cut 
    let key = []; 
     
    // To represent set of vertices included in MST 
    let mstSet = []; 
 
    // Initialize all keys as INFINITE 
    for
                          (let i = 0; i < V; i++) 
        key[i] = Number.MAX_VALUE, mstSet[i] = false; 
 
    // Always include first 1st vertex in MST. 
    // Make key 0 so that this vertex is picked as first vertex. 
    key[0] = 0; 
    parent[0] = -1; // First node is always root of MST 
 
    // The MST will have V vertices 
    for
                          (let count = 0; count < V - 1; count++)
    { 
        // Pick the minimum key vertex from the 
        // set of vertices not yet included in MST 
        let u = minKey(key, mstSet); 
 
        // Add the picked vertex to the MST Set 
        mstSet[u] = true; 
 
        // Update key value and parent index of 
        // the adjacent vertices of the picked vertex. 
        // Consider only those vertices which are not 
        // yet included in MST 
        for (let v = 0; v < V; v++) 
 
            // graph[u][v] is non zero only for adjacent vertices of m 
            // mstSet[v] is false for vertices not yet included in MST 
            // Update the key only if graph[u][v] is smaller than key[v] 
            if (graph[u][v] && mstSet[v] == false
                          && graph[u][v] < key[v]) 
                parent[v] = u, key[v] = graph[u][v]; 
    } 
 
    // print the constructed MST 
    printMST(parent, graph); 
} 
 
// Driver code
     
let graph = [ [ 0, 2, 0, 6, 0 ], 
[ 2, 0, 3, 8, 5 ], 
[ 0, 3, 0, 0, 7 ], 
[ 6, 8, 0, 0, 9 ], 
[ 0, 5, 7, 9, 0 ] ]; 
 
// Print the solution 
                        
primMST(graph); 
 
 
// This code is contributed by Dharanendra L V.
</script>

                  

              
            

输出

时间复杂度： O(V ² )，如果输入图使用邻接表表示，那么Prim算法的时间复杂度可以借助二叉堆降低到O(E * logV)。在这个实现中，我们总是考虑生成树从图的根开始
辅助空间： O(V)

Prim算法的其他实现：

下面给出了 Prim 算法的一些其他实现

用于邻接矩阵表示的 Prim 算法 – 在本文中，我们讨论了在图由邻接矩阵表示的情况下实现 Prim 算法的方法。
Prim 的邻接列表表示算法 – 在本文中，Prim 的算法实现针对由邻接列表表示的图进行了描述。
使用优先级队列的 Prim 算法：在本文中，我们讨论了一种实现 Prim 算法的省时方法。

PRIM算法的优化方法：

直觉

我们使用ArrayList<ArrayList<Integer>> 将邻接矩阵转换为邻接列表。

然后我们创建一个 Pair 类来存储顶点及其权重。

我们根据最低权重对列表进行排序。

我们创建优先级队列并将第一个顶点及其权重推入队列中

然后我们遍历它的边并将最小的权重存储在一个名为 ans 的变量中。

最后，在所有顶点之后，我们返回 ans。

执行

C++
Java
Python3

C++

              
                
                    #include<bits/stdc++.h>
using namespace std;
 
typedef pair<int,int> pii;
 
// Function to find sum of weights of edges of the Minimum Spanning Tree.
                        
int spanningTree(int V, int E, int edges[][3])
{   
    // Create an adjacency list representation of the graph
    vector<vector<int>> adj[V];
     
    // Fill the adjacency list with edges and their weights
    for (int i = 0; i < E; i++) {
        int u = edges[i][0];
        int v = edges[i][1];
        int wt = edges[i][2];
        adj[u].push_back({v, wt});
        adj[v].push_back({u, wt});
    }
     
    // Create a priority queue to store edges with their weights
    priority_queue<pii, vector<pii>, greater<pii>> pq;
                        
     
    // Create a visited array to keep track of visited vertices
    vector<bool> visited(V, false);
     
    // Variable to store the result (sum of edge weights)
    int
                          res = 0;
     
    // Start with vertex 0
    pq.push({0, 0});
     
    // Perform Prim's algorithm to find the Minimum Spanning Tree
    while(!pq.empty()){
        auto p = pq.top();
        pq.pop();
         
        int wt = p.first;  // Weight of the edge
        int u = p.second;  // Vertex connected to the edge
         
        if(visited[u] == true){
            continue;  // Skip if the vertex is already visited
        }
         
        res += wt;  // Add the edge weight to the result
        visited[u] = true;  // Mark the vertex as visited
                        
         
        // Explore the adjacent vertices
        for(auto v : adj[u]){
            // v[0] represents the vertex and v[1] represents the edge weight
                        
            if(visited[v[0]] == false){
                pq.push({v[1], v[0]});  // Add the adjacent edge to the priority queue
            }
        }
    }
     
    return res;  // Return the sum of edge weights of the Minimum Spanning Tree
}
 
int main()
{
    int
                          graph[][3] = {{0, 1, 5},
                      {1, 2, 3},
                      {0, 2, 1}};
 
    // Function call
    cout << spanningTree(3, 3, graph) << endl;
 
    return 0;
}

                  

              
            

Java

              
                
                    // A Java program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency list
// representation of the graph
 
import java.io.*;
import java.util.*;
 
// Class to form pair
class Pair implements Comparable<Pair>
{
    int
                          v;
    int
                          wt;
    Pair(int v,int wt)
    {
        this.v=v;
        this.wt=wt;
    }
    public
                          int compareTo(Pair that)
    {
        return this.wt-that.wt;
    }
}
 
class GFG {
 
// Function of spanning tree
static int spanningTree(int V, int
                          E, int edges[][])
    {
         ArrayList<ArrayList<Pair>> adj=new ArrayList<>();
         for(int i=0;i<V;i++)
                        
         {
             adj.add(new ArrayList<Pair>());
         }
         for(int i=0;i<edges.length;i++)
         {
             int u=edges[i][0];
             int v=edges[i][1];
             int wt=edges[i][2];
             adj.get(u).add(new Pair(v,wt));
             adj.get(v).add(new Pair(u,wt));
         }
         PriorityQueue<Pair> pq = new PriorityQueue<Pair>();
         pq.add(new Pair(0,0));
         int[] vis=new
                          int[V];
         int s=0;
         while(!pq.isEmpty())
         {
             Pair node=pq.poll();
             int v=node.v;
             int wt=node.wt;
             if(vis[v]==1) 
             continue;
              
                        
             s+=wt;
             vis[v]=1;
             for(Pair it:adj.get(v))
             {
                 if(vis[it.v]==0)
                 {
                     pq.add(new Pair(it.v,it.wt));
                 }
             }
         }
         return s;
    }
     
    // Driver code
    public
                          static void main (String[] args) {
        int graph[][] = new int[][] {{0,1,5},
                                    {1,2,3},
                                    {0,2,1}};
  
        // Function call
        System.out.println(spanningTree(3,3,graph));
    }
}

                  

              
            

Python3

              
                
                    import heapq
 
def tree(V, E, edges):
    # Create an adjacency list representation of the graph
    adj = [[] for
                          _ in range(V)]
    # Fill the adjacency list with edges and their weights
    for
                          i in range(E):
        u, v, wt = edges[i]
        adj[u].append((v, wt))
        adj[v].append((u, wt))
    # Create a priority queue to store edges with their weights
    pq = []
    # Create a visited array to keep track of visited vertices
    visited = [False] * V
    # Variable to store the result (sum of edge weights)
    res = 0
    # Start with vertex 0
    heapq.heappush(pq, (0, 0))
    # Perform Prim's algorithm to find the Minimum Spanning Tree
    while
                          pq:
        wt, u = heapq.heappop(pq)
        if visited[u]:
            continue 
            # Skip if the vertex is already visited
        res += wt  
        # Add the edge weight to the result
        visited[u] = True 
        # Mark the vertex as visited
        # Explore the adjacent vertices
        for v, weight in adj[u]:
            if not visited[v]:
                heapq.heappush(pq, (weight, v))  
                # Add the adjacent edge to the priority queue
    return
                          res  
  # Return the sum of edge weights of the Minimum Spanning Tree
if __name__ ==
                          "__main__":
    graph = [[0, 1, 5],
             [1, 2, 3],
             [0, 2, 1]]
    # Function call
    print(tree(3, 3, graph))

                  

              
            

输出

时间复杂度： O(E*log(E))，其中 E 是边数
辅助空间： O(V^2)，其中 V 是顶点数

Prim 寻找最小生成树（MST）的算法：

优点：

Prim 的算法保证在连通的加权图中找到 MST。
使用二叉堆或斐波那契堆的时间复杂度为 O(E log V)，其中 E 是边数，V 是顶点数。
与其他一些 MST 算法相比，它是一种易于理解和实现的相对简单的算法。

缺点：

与 Kruskal 算法一样，Prim 算法在具有许多边的密集图上可能会很慢，因为它需要对所有边至少迭代一次。
Prim 的算法依赖于优先级队列，这会占用额外的内存并在非常大的图上减慢算法的速度。
起始节点的选择会影响 MST 输出，这在某些应用中可能是不可取的。

Prim(普里姆)算法 可视化交互式动画版

Prim的算法简介：

Prim 算法如何工作？

Prim算法说明：

如何实现Prim算法？

C++

C

Java

Python3

C#

Javascript

Prim算法的其他实现：

PRIM算法的优化方法：

C++

Java

Python3

Prim 寻找最小生成树（MST）的算法：

优点：

缺点：

Prim(普里姆)算法可视化交互式动画版