正在载入交互式动画窗口请稍等
哈希表-拉链法 可视化交互式动画版

哈希表是最重要的数据结构之一,它使用称为哈希函数的特殊函数,将给定值与键映射以更快地访问元素。
哈希表是一种存储一些信息的数据结构,这些信息基本上有两个主要组成部分,即键和值。 哈希表可以借助关联数组来实现。 映射的效率取决于用于映射的散列函数的效率。
例如,假设键值为 John,值为电话号码,那么当我们将键值传递到哈希函数中时,如下所示:
哈希(键)=索引;
当我们在哈希函数中传递键时,它就会给出索引。
哈希(约翰)= 3;
上面的示例在索引 3 处添加了 john。
哈希函数的缺点
哈希函数为每个值分配一个唯一的键。 有时哈希表使用不完美的哈希函数会导致冲突,因为哈希函数生成两个不同值的相同键。
散列
散列是使用恒定时间的搜索技术之一。 哈希的时间复杂度是 O(1)。 到目前为止,我们了解了两种搜索技术,即 线性搜索 和 二分搜索 。 线性搜索的最差时间复杂度为 O(n),二分搜索的最差时间复杂度为 O(logn)。 在这两种搜索技术中,搜索取决于元素的数量,但我们希望该技术需要恒定的时间。 因此,提供恒定时间的哈希技术应运而生。
在哈希技术中,使用哈希表和哈希函数。 使用哈希函数,我们可以计算出可以存储该值的地址。
散列背后的主要思想是创建(键/值)对。 如果给出了密钥,则算法将计算存储该值的索引。 可以写成:
索引 = 哈希(键)
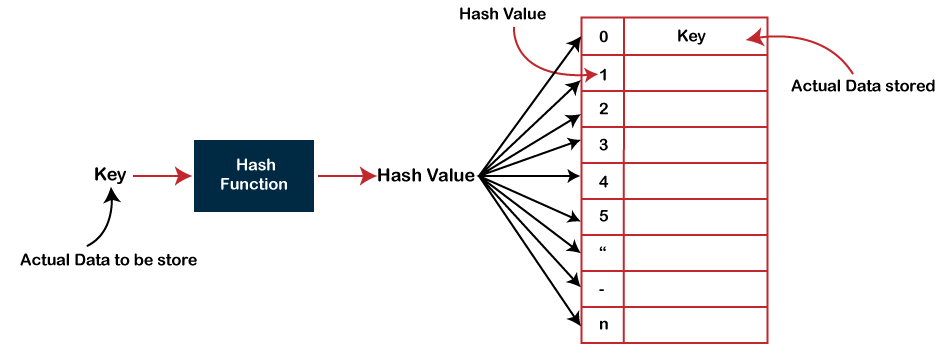
哈希函数的计算方式有以下三种:
- 划分方法
- 折叠方式
- 中方法
在除法中,哈希函数可以定义为:
h(ki ) =ki % m;
其中 m 是哈希表的大小。
例如,如果键值为 6,哈希表的大小为 10。当我们将哈希函数应用于键 6 时,索引将为:
h(6) = 6%10 = 6
存储该值的索引为 6。
碰撞
当两个不同的值具有相同的值时,两个值之间就会出现问题,称为冲突。 在上面的示例中,该值存储在索引 6 处。如果键值为 26,则索引将为:
h(26) = 26%10 = 6
因此,两个值存储在相同的索引处,即6,这会导致冲突问题。 为了解决这些冲突,我们有一些称为碰撞技术的技术。
以下是碰撞技巧:
- 开放散列:也称为封闭寻址。
- 封闭散列:也称为开放寻址。
开放散列
在开放散列中,用于解决冲突的方法之一称为链接方法。
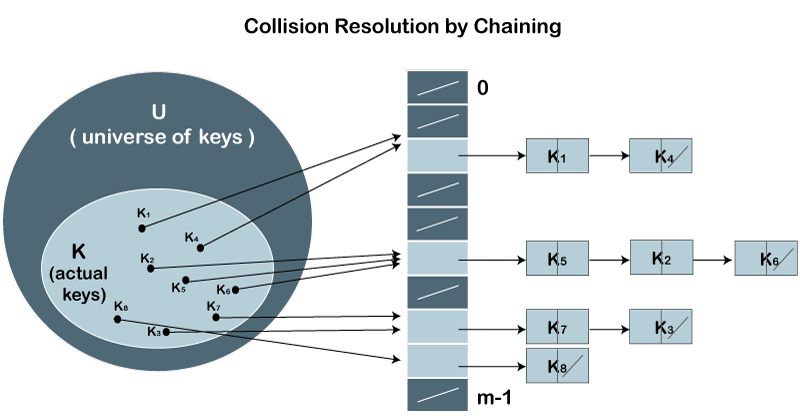
让我们首先了解解决冲突的链接。
假设我们有一个键值列表
A = 3, 2, 9, 6, 11, 13, 7, 12,其中 m = 10,且 h(k) = 2k+3
在这种情况下,我们不能直接使用 h(k) = k i /m 作为 h(k) = 2k+3
- 键值3的索引为:
索引 = h(3) = (2(3)+3)%10 = 9
值 3 将存储在索引 9 处。
- 键值2的索引为:
索引 = h(2) = (2(2)+3)%10 = 7
值 2 将存储在索引 7 处。
- 键值9的索引为:
索引 = h(9) = (2(9)+3)%10 = 1
值 9 将存储在索引 1 处。
- 键值6的索引为:
索引 = h(6) = (2(6)+3)%10 = 5
值 6 将存储在索引 5 处。
- 键值11的索引为:
索引 = h(11) = (2(11)+3)%10 = 5
值 11 将存储在索引 5 处。现在,我们有两个值 (6, 11) 存储在同一个索引处,即 5。这会导致冲突问题,因此我们将使用链接方法来避免冲突。 我们将再创建一个列表并将值 11 添加到该列表中。 创建新列表后,新创建的列表将链接到值为 6 的列表。
- 键值13的索引为:
索引 = h(13) = (2(13)+3)%10 = 9
值 13 将存储在索引 9 处。现在,我们有两个值 (3, 13) 存储在同一个索引处,即 9。这会导致冲突问题,因此我们将使用链接方法来避免冲突。 我们将再创建一个列表并将值 13 添加到该列表中。 创建新列表后,新创建的列表将链接到值为 3 的列表。
- 键值7的索引为:
索引 = h(7) = (2(7)+3)%10 = 7
值 7 将存储在索引 7 处。现在,我们有两个值 (2, 7) 存储在同一索引处,即 7。这会导致冲突问题,因此我们将使用链接方法来避免冲突。 我们将再创建一个列表并将值 7 添加到该列表中。 创建新列表后,新创建的列表将链接到值为 2 的列表。
- 键值12的索引为:
索引 = h(12) = (2(12)+3)%10 = 7
根据上面的计算,值 12 必须存储在索引 7 处,但值 2 存在于索引 7 处。因此,我们将创建一个新列表并将 12 添加到列表中。 新创建的列表将链接到值为 7 的列表。
计算出的每个键值关联的索引值如下表所示:
| 钥匙 | 地点(u) |
| 3 | ((2*3)+3)%10 = 9 |
| 2 | ((2*2)+3)%10 = 7 |
| 9 | ((2*9)+3)%10 = 1 |
| 6 | ((2*6)+3)%10 = 5 |
| 11 | ((2*11)+3)%10 = 5 |
| 13 | ((2*13)+3)%10 = 9 |
| 7 | ((2*7)+3)%10 = 7 |
| 12 | ((2*12)+3)%10 = 7 |
封闭散列
在封闭散列中,使用三种技术来解决冲突:
- 线性探测
- 二次探测
- 双哈希技术
线性探测
线性探测是开放寻址的形式之一。 我们知道哈希表中的每个单元都包含一个键值对,因此当通过将新键映射到已被另一个键占用的单元而发生冲突时,线性探测技术会搜索最近的空闲位置并添加新的那个空单元格的钥匙。 此时,从发生冲突的位置开始依次搜索,直到找不到空单元为止。
让我们通过一个例子来理解线性探测。
考虑上面的线性探测示例:
A = 3, 2, 9, 6, 11, 13, 7, 12,其中 m = 10,且 h(k) = 2k+3
键值3、2、9、6分别存储在索引9、7、1、5处。 计算出的索引值11是5,它已经被另一个键值6占用。当应用线性探测时,距离索引5最近的空单元格是6; 因此,值 11 将添加到索引 6 处。
下一个键值是13。当应用散列函数时,与该键值关联的索引值是9。 该单元格已在索引 9 处填充。应用线性探测时,距离索引 9 最近的空单元格为 0; 因此,值 13 将添加到索引 0 处。
下一个键值是7。当应用散列函数时,与该键值关联的索引值是7。 该单元格已在索引 7 处填充。应用线性探测时,距离索引 7 最近的空单元格是 8; 因此,值 7 将添加到索引 8 处。
下一个键值是12。当应用散列函数时,与该键值关联的索引值是7。 该单元格已在索引 7 处填充。应用线性探测时,距离索引 7 最近的空单元格为 2; 因此,值 12 将添加到索引 2 处。
二次探测
在线性探测的情况下,搜索是线性执行的。 相反,二次探测是一种开放寻址技术,它使用二次多项式进行搜索,直到找到空槽。
还可以将其定义为允许在从(u+i 2 )%m(其中i=0到m-1 )的第一个空闲位置处插入ki 。
让我们通过一个例子来理解二次探测。
考虑我们在线性探测中讨论的相同示例。
A = 3, 2, 9, 6, 11, 13, 7, 12,其中 m = 10,且 h(k) = 2k+3
键值3、2、9、6分别存储在索引9、7、1、5处。 我们不需要对这些关键值应用二次探测技术,因为不会发生冲突。
11的索引值为5,但是这个位置已经被6占据了。因此,我们应用二次探测技术。
当我=0时
指数= (5+0 2 )%10 = 5
当i=1时
索引 = (5+1 2 )%10 = 6
由于位置 6 为空,因此将在索引 6 处添加值 11。
下一个元素是 13。当对 13 应用哈希函数时,索引值为 9,这我们已经在链接方法中讨论过。 在索引 9 处,单元格被另一个值(即 3)占用。因此,我们将应用二次探测技术来计算空闲位置。
当i=0时
索引 = (9+0 2 )%10 = 9
当i=1时
索引 = (9+1 2 )%10 = 0
由于位置 0 为空,因此将在索引 0 处添加值 13。
下一个元素是 7。当对 7 应用哈希函数时,索引值为 7,这我们已经在链接方法中讨论过。 在索引 7 处,单元格被另一个值(即 7)占用。因此,我们将应用二次探测技术来计算空闲位置。
当i=0时
索引 = (7+0 2 )%10 = 7
当i=1时
索引 = (7+1 2 )%10 = 8
由于位置 8 为空,因此将在索引 8 处添加值 7。
下一个元素是 12。当对 12 应用哈希函数时,索引值为 7。当我们观察哈希表时,我们会知道索引 7 处的单元格已经被值 2 占用因此,我们对 12 应用二次探测技术来确定空闲位置。
当i=0时
指数= (7+0 2 )%10 = 7
当i=1时
索引 = (7+1 2 )%10 = 8
当i=2时
索引 = (7+2 2 )%10 = 1
当i=3时
索引 = (7+3 2 )%10 = 6
当i=4时
索引 = (7+4 2 )%10 = 3
由于位置 3 为空,因此值 12 将存储在索引 3 处。
最终的哈希表将是:
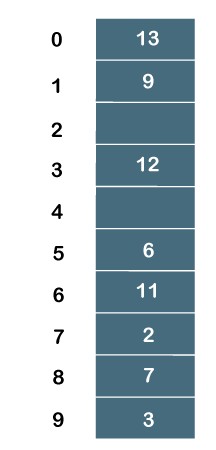
因此,元素的顺序为 13, 9, _, 12, _, 6, 11, 2, 7, 3。
双重哈希
双散列是一种开放寻址技术,用于避免冲突。 当发生冲突时,该技术使用密钥的二级哈希。 它使用一个哈希值作为索引向前移动,直到找到空位置。
在双重哈希中,使用两个哈希函数。 假设h 1 (k)是用于计算位置的哈希函数之一,而h 2 (k)是另一个哈希函数。 它可以定义为“ 在 (u+v*i)%m 的第一个空闲位置插入 k i ,其中 i=(0 到 m-1)”。 在这种情况下,u是使用哈希函数计算的位置,v等于(h 2 (k)%m)。
考虑我们在二次探测中使用的相同示例。
A = 3, 2, 9, 6, 11, 13, 7, 12,其中 m = 10,并且
h 1 (k) = 2k+3
h 2 (k) = 3k+1
| 钥匙 | 地点(你) | v | 探测 |
| 3 | ((2*3)+3)%10 = 9 | - | 1 |
| 2 | ((2*2)+3)%10 = 7 | - | 1 |
| 9 | ((2*9)+3)%10 = 1 | - | 1 |
| 6 | ((2*6)+3)%10 = 5 | - | 1 |
| 11 | ((2*11)+3)%10 = 5 | (3(11)+1)%10 =4 | 3 |
| 13 | ((2*13)+3)%10 = 9 | (3(13)+1)%10 = 0 | |
| 7 | ((2*7)+3)%10 = 7 | (3(7)+1)%10 = 2 | |
| 12 | ((2*12)+3)%10 = 7 | (3(12)+1)%10 = 7 | 2 |
我们知道插入键 (3, 2, 9, 6) 时不会发生冲突,因此我们不会对这些键值应用双重哈希。
将键 11 插入哈希表时,会发生冲突,因为计算出的 11 的索引值为 5,该值已被其他值占用。 因此,我们将对键11应用双重哈希技术。当键值为11时,v的值为4。
现在,将 u 和 v 的值代入 (u+v*i)%m
当i=0时
索引 = (5+4*0)%10 =5
当i=1时
索引 = (5+4*1)%10 = 9
当i=2时
索引 = (5+4*2)%10 = 3
由于哈希表中位置 3 为空; 因此,键 11 添加到索引 3 处。
下一个元素是 13。计算出的 13 的索引值是 9,它已经被另一个键值占用。 因此,我们将使用双重哈希技术来查找空闲位置。 v 的值为 0。
现在,将 u 和 v 的值代入 (u+v*i)%m
当i=0时
索引 = (9+0*0)%10 = 9
当 v 的值为零时,我们将在从 0 到 m-1 的所有迭代中得到 9 个值。 因此,我们不能将13插入到哈希表中。
下一个元素是 7。计算出的 7 的索引值是 7,它已经被另一个键值占用。 因此,我们将使用双重哈希技术来查找空闲位置。 v 的值为 2。
现在,将 u 和 v 的值代入 (u+v*i)%m
当i=0时
索引 = (7 + 2*0)%10 = 7
当i=1时
索引 = (7+2*1)%10 = 9
当i=2时
索引 = (7+2*2)%10 = 1
当i=3时
索引 = (7+2*3)%10 = 3
当i=4时
索引 = (7+2*4)%10 = 5
当i=5时
索引 = (7+2*5)%10 = 7
当i=6时
索引 = (7+2*6)%10 = 9
当i=7时
索引 = (7+2*7)%10 = 1
当i=8时
索引 = (7+2*8)%10 = 3
当i=9时
索引 = (7+2*9)%10 = 5
由于我们检查了 i 的所有情况(从 0 到 9),但是我们没有找到合适的位置插入 7。因此,键 7 不能插入到哈希表中。
下一个元素是 12。计算出的 12 的索引值是 7,它已经被另一个键值占用。 因此,我们将使用双重哈希技术来查找空闲位置。 v 的值为 7。
现在,将 u 和 v 的值代入 (u+v*i)%m
当i=0时
索引 = (7+7*0)%10 = 7
当i=1时
索引 = (7+7*1)%10 = 4
由于位置4是空的; 因此,键 12 被插入到索引 4 处。
最终的哈希表将是:
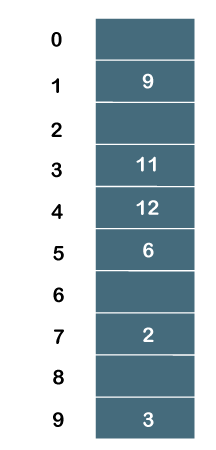
元素的顺序为_、9、_、11、12、6、_、2、_、3。