线索二叉树可视化交互式动画版

线索二叉树是一种二叉树数据结构，其中二叉树中的空左右子指针被替换为将节点直接链接到其有序前驱或后继的线索，从而提供了一种无需遍历树的方法。使用递归或堆栈。

二叉树的中序遍历可以使用递归或使用辅助堆栈来完成。线索二叉树的想法是使中序遍历更快，并且无需堆栈且无需递归。通过将通常为 NULL 的所有右子指针指向该节点的中序后继节点（如果存在），可以使二叉树成为线索化的。

当需要考虑空间时，线索二叉树会很有用，因为它们可以消除遍历过程中对堆栈的需要。然而，它们的实现比标准二叉树更复杂。

有两种类型的线索二叉树。
单线索： 其中 NULL 右指针指向中序后继者（如果后继者存在）
双线索： 其中左和右 NULL 指针分别指向中序前任者和中序后继者。前驱线索对于逆序遍历和后序遍历很有用。
线索对于快速访问节点的祖先也很有用。
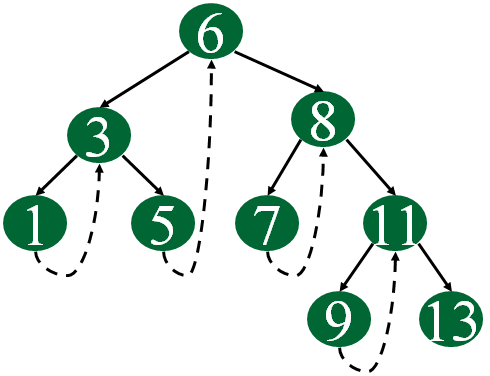
下图显示了一个单线索二叉树示例。虚线代表线索。

线索BT

线索节点的 C 和 C++ 表示
下面是单线索节点的 C 和 C++ 表示。

C

              
                    struct Node 
{
    int
                          data;
    struct Node *left, *right;
    bool rightThread;  
}

C++

              
                
                    // Use any below method to represent a Threaded Node
 
// Method 1: Using "struct" to make
// user-define data type
                        
struct node {
    int
                          data;
    struct node* left;
    struct node* right;
    bool rightThread;
};
 
// Method 2: Using "class" to make
// user-define data type
                        
class Node {
public:
    int
                          data;
    Node* left;
    Node* right;
    bool rightThread;
    // Val is the key or the value that has to be added to
    // the data part
    Node(int val){
        data = val;
        // Left and right child for node will be initialized
        // to null
        left = NULL;
        right = NULL;
        // rightThread will be initialized to false
        rightThread = false;
    }
};
 
// This code is contributed by Susobhan Akhuli

                  

              
            

线索节点的 Java 表示

以下是单线索节点的 Java 表示。

Java

Java

              
                    static class Node 
{
    int
                          data;
    Node left, right;
    boolean
                          rightThread;  
}
 
// This code contributed by aashish1995

由于右指针有两个用途，因此布尔变量 rightThread 用于指示右指针是否指向右孩子或中序后继。类似地，我们可以为双线索二叉树添加 leftThread。
使用线索进行中序遍历
以下是线索二叉树中中序遍历的代码。

C++

              
                
                    // Utility function to find leftmost node in a tree rooted with n
                        
Node* leftMost(Node* n){
    if
                          (n == NULL)
        return NULL;
 
    while (n->left != NULL)
        n = n->left;
 
    return n;
}
 
// CPP code to do inorder traversal in a threaded binary tree
void inOrder(Node* root){
    Node* cur = leftMost(root);
    while (cur != NULL) {
        cout<<cur->data<<" ";
 
        // If this node is a thread node, then go to
        // inorder successor
        if (cur->rightThread)
            cur = cur->right;
        else // Else go to the leftmost child in right
             // subtree
            cur = leftmost(cur->right);
    }
}
 
// This code is contributed by Susobhan Akhuli

                  

              
            

C

              
                
                    // Utility function to find leftmost node in a tree rooted
// with n
struct Node* leftMost(struct Node* n)
{
    if
                          (n == NULL)
        return NULL;
 
    while (n->left != NULL)
        n = n->left;
 
    return n;
}
 
// C code to do inorder traversal in a threaded binary tree
void inOrder(struct Node* root)
{
    struct Node* cur = leftMost(root);
                        
    while (cur != NULL) {
        printf("%d ", cur->data);
 
        // If this node is a thread node, then go to
        // inorder successor
        if (cur->rightThread)
            cur = cur->right;
        else // Else go to the leftmost child in right
             // subtree
            cur = leftmost(cur->right);
    }
}

                  

              
            

Java

              
                
                    // Utility function to find leftmost node in a tree rooted
// with n
Node leftMost(Node n)
{
    if
                          (n == null)
                        
        return null;
                        
 
    while
                          (n.left != null)
        n = n.left;
 
    return
                          n;
}
 
// C code to do inorder traversal in a threaded binary tree
static void inOrder(Node root)
{
    Node cur = leftMost(root);
    while
                          (cur != null) {
        System.out.printf("%d ", cur.data);
 
        // If this node is a thread node, then go to
        // inorder successor
        if (cur.rightThread)
            cur = cur.right;
        else // Else go to the leftmost child in right
             // subtree
            cur = leftmost(cur.right);
    }
}
 
// This code contributed by aashish1995

                  

              
            

Python3

              
                
                    # Utility function to find leftmost Node in a tree rooted
# with n
def leftMost(n):
 
    if
                          (n ==
                          None):
        return None;
                        
 
    while
                          (n.left != None):
        n = n.left;
                        
 
    return
                          n;
 
 
# C code to do inorder traversal in a threaded binary tree
def inOrder(root):
 
    cur = leftMost(root);
    while
                          (cur != None):
        print(cur.data," ");
 
        # If this Node is a thread Node, then go to
        # inorder successor
        if (cur.rightThread):
            cur = cur.right;
        else: # Else go to the leftmost child in right
             # subtree
            cur = leftmost(cur.right);
 
# This code is contributed by Rajput-Ji 

                  

              
            

C＃

              
                
                    // Utility function to find leftmost node in a tree rooted
// with n
Node leftMost(Node n)
{
  if (n == null)
    return
                          null;
 
  while (n.left != null)
    n = n.left;
 
  return n;
}
 
// C code to do inorder traversal in a threaded binary tree
static void inOrder(Node root)
{
  Node cur = leftMost(root);
  while (cur != null) 
  {
    Console.Write("{0} ", cur.data);
 
    // If this node is a thread node, then go to
    // inorder successor
    if
                          (cur.rightThread)
      cur = cur.right;
    else
                          // Else go to the leftmost child in right
      // subtree
      cur = leftmost(cur.right);
  }
}
 
// This code is contributed by gauravrajput1

                  

              
            

JavaScript

              
                
                    <script>
 
// Utility function to find leftmost node in a tree rooted
// with n
function leftMost(n)
{
    if
                          (n == null)
                        
        return null;
                        
  
    while
                          (n.left != null)
        n = n.left;
  
    return
                          n;
}
 
// JavaScript code to do inorder traversal in 
// a threaded binary tree
                        
function inOrder(root)
{
    let cur = leftMost(root);
    while
                          (cur != null) {
        document.write(cur.data+" ");
  
        // If this node is a thread node, then go to
        // inorder successor
        if (cur.rightThread)
            cur = cur.right;
        else // Else go to the leftmost child in right
             // subtree
            cur = leftmost(cur.right);
        }
}
 
// This code is contributed by unknown2108
 
</script>

                  

              
            

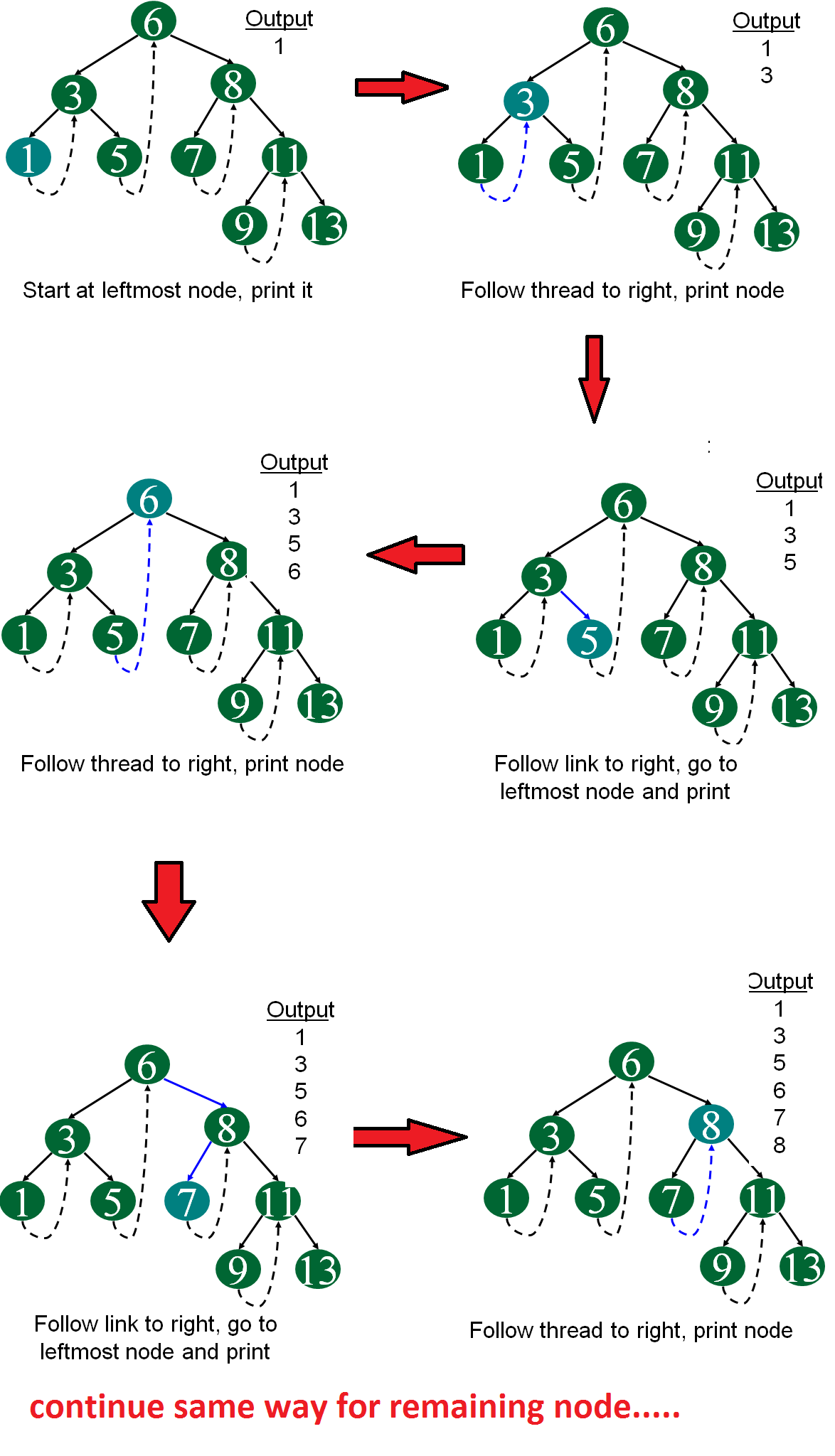
下图演示了使用线索进行中序遍历。

线索遍历

线索二叉树的优点

在这棵树中，它可以实现元素的线性遍历。
它在执行线性遍历时消除了堆栈的使用，因此节省了内存。
无需显式使用父指针即可找到父节点
线索树按顺序方式向前和向后遍历节点
节点包含指向有序前驱和后继的指针
对于给定的节点，我们可以轻松找到有序的前驱节点和后继节点。因此，搜索变得更加容易。
在线索二叉树中不存在 NULL 指针。因此，避免了占用 NULL 链接的内存浪费。
线索指向后继节点和前驱节点。这使得我们能够快速获得任意节点的前驱节点和后继节点。
遍历树时不需要堆栈，因为使用线索链接我们可以到达之前访问过的节点。

线索二叉树的缺点

线索二叉树中的每个节点都需要额外的信息（额外的内存）来指示其左节点或右节点是否指示其子节点或其有序前驱或后继。因此，该节点需要消耗额外的内存来实现。
插入和删除比普通插入和删除更加复杂和耗时，因为需要维护线索和普通链接。
为每个可能的节点实现线索很复杂。
复杂性增加：实现线索二叉树需要比常规二叉树更复杂的算法和数据结构。这会使代码更难阅读和调试。
额外的内存使用：在某些情况下，用于线索树的附加指针可能比常规二叉树占用更多的内存。如果树不完全平衡，则尤其如此，因为对倾斜的树进行线索化可能会导致大量额外的指针。
灵活性有限：线索二叉树是针对特定类型的遍历进行优化的专用数据结构。虽然对于这些类型的操作来说它们比常规二叉树更有效，但它们在其他场景中可能没有那么有用。例如，它们不能在不破坏线索的情况下轻松修改（例如插入或删除节点）。
并行化困难：在线索二叉树上并行化操作可能具有挑战性，因为线索可能会引入数据依赖性，从而难以独立处理节点。这可能会限制通过并行性实现的性能提升。

线索二叉树的应用 –

表达式求值：线索二叉树可用于以避免递归或堆栈的方式求算算术表达式。可以根据输入表达式构造树，然后按顺序或预顺序遍历以执行评估。
数据库索引：在数据库中，线索二叉树可用于根据特定字段（例如姓氏）对数据进行索引。可以使用索引值作为键来构造树，然后按顺序遍历以按排序顺序检索数据。
符号表管理：在编译器或解释器中，线索二叉树可用于存储和管理变量和函数的符号表。可以用符号作为键来构建树，然后按顺序或预顺序遍历以对符号表执行各种操作。
基于磁盘的数据结构：线索二叉树可用于基于磁盘的数据结构（例如B树）以提高性能。通过对树进行线索化，可以以最小化磁盘查找并提高引用局部性的方式遍历它。
分层数据的导航：在某些应用程序中，线索二叉树可用于导航分层数据结构，例如文件系统或网站目录。可以根据分层数据构建树，然后按顺序或预顺序遍历以按特定顺序有效地访问数据。

我们很快将讨论线索二叉树中的插入和删除。
来源：
http ://en.wikipedia.org/wiki/Threaded_binary_tree
www.cs.berkeley.edu/~kamil/teaching/su02/080802.ppt
如果您发现任何不正确的内容，或者您想分享更多相关信息，请发表评论上面讨论的主题

线索二叉树 可视化交互式动画版

C

C++

Java

C++

C

Java

Python3

C＃

JavaScript

线索二叉树的应用 –

线索二叉树可视化交互式动画版