简单选择排序可视化交互式动画版

选择排序 是一种简单而高效的排序算法，其工作原理是重复从列表的未排序部分中选择最小（或最大）元素并将其移动到列表的已排序部分。

该算法重复从列表的未排序部分中选择最小（或最大）元素，并将其与未排序部分的第一个元素交换。对剩余的未排序部分重复此过程，直到整个列表排序完毕。

选择排序算法如何工作？

让我们以以下数组为例： arr[] = {64, 25, 12, 22, 11}

第一遍：

对于排序数组中的第一个位置，从索引 0 到 4 顺序遍历整个数组。 当前存储64 的第一个位置，遍历整个数组后很明显 11 是最低值。

因此，将 64 替换为 11。一次迭代后， 11 （恰好是数组中的最小值）往往会出现在排序列表的第一个位置。

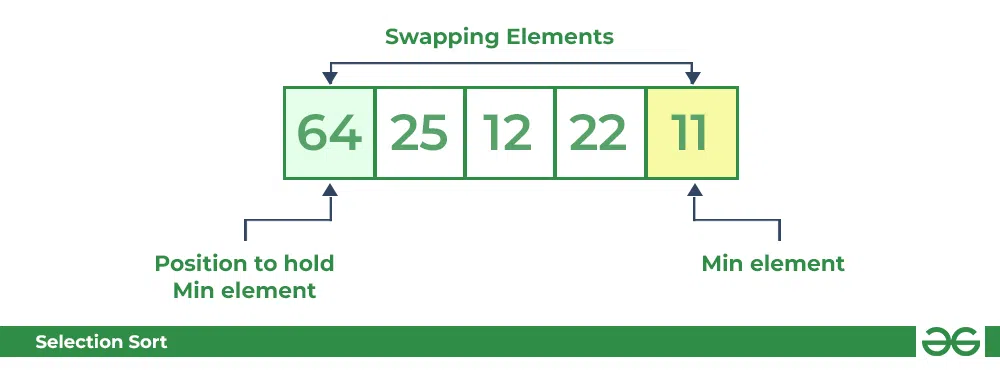
选择排序算法 | 将第一个元素与数组中的最小值交换

第二遍：

对于存在 25 的第二个位置，再次按顺序遍历数组的其余部分。

遍历完后，我们发现 12 是数组中倒数第二小的值，它应该出现在数组的第二位，因此交换这些值。

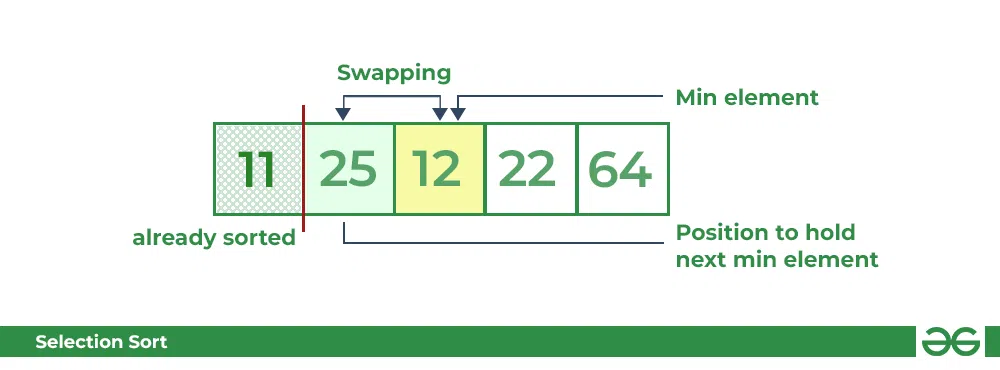
选择排序算法 | 将 i=1 与下一个最小元素交换

第三遍：

现在，对于第三个位置，其中存在 25， 再次遍历数组的其余部分并找到数组中存在的第三个最小值。

遍历时， 22 是第三个最小值，它应该出现在数组中的第三个位置，因此将 22 与第三个位置上的元素交换。

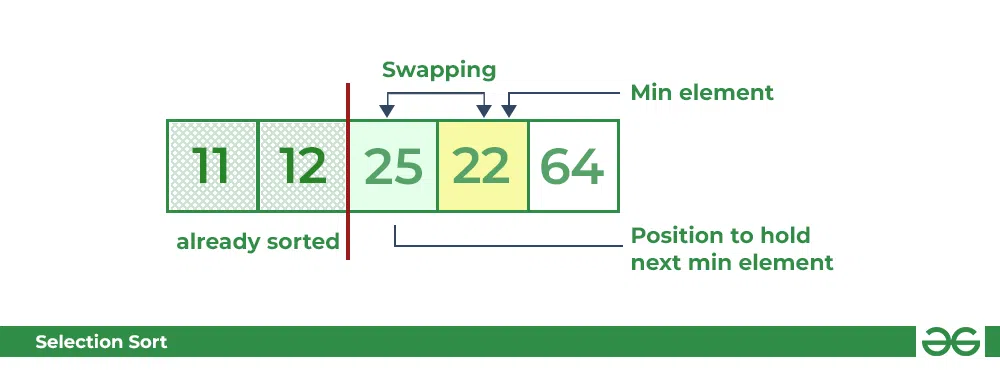
选择排序算法 | 将 i=2 与下一个最小元素交换

第四遍：

类似地，对于第四个位置，遍历数组的其余部分并找到数组中第四小的元素

由于 25 是第四低的值，因此它将排在第四位。

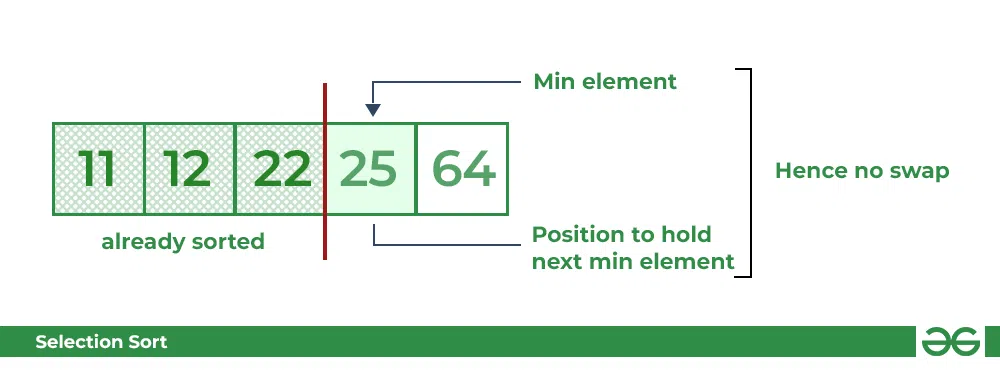
选择排序算法 | 将 i=3 与下一个最小元素交换

第五关：

最后，数组中存在的最大值自动放置在数组的最后一个位置

结果数组是排序后的数组。

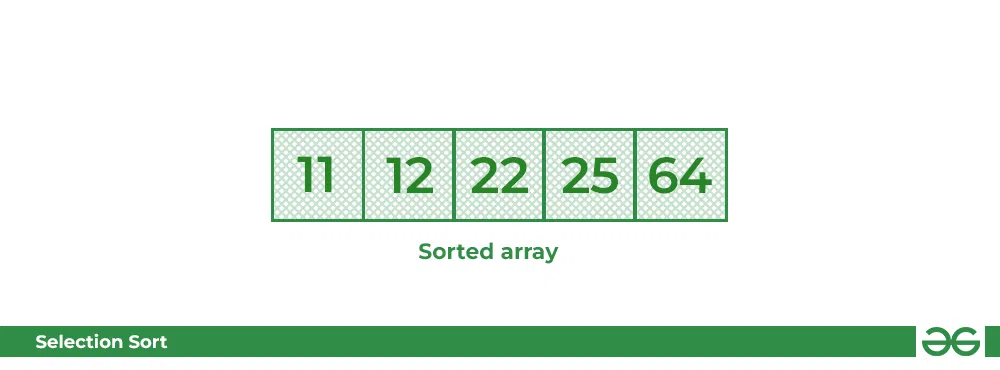
选择排序算法 | 需要排序的数组

下面是上述方法的实现：

C++

              
                
                    // C++ program for implementation of
// selection sort
#include <bits/stdc++.h>
using namespace std;
 
// Function for Selection sort
void selectionSort(int arr[], int n)
{
    int
                          i, j, min_idx;
 
    // One by one move boundary of
    // unsorted subarray
    for (i = 0; i < n - 1; i++) {
                        
 
        // Find the minimum element in
        // unsorted array
        min_idx = i;
        for (j = i + 1; j < n; j++) {
                        
            if (arr[j] < arr[min_idx])
                min_idx = j;
        }
 
        // Swap the found minimum element
        // with the first element
        if (min_idx != i)
            swap(arr[min_idx], arr[i]);
    }
}
 
// Function to print an array
void printArray(int arr[], int size)
{
    int
                          i;
    for (i = 0; i < size; i++) {
        cout << arr[i] << " ";
        cout << endl;
    }
}
 
// Driver program
int main()
{
    int
                          arr[] = { 64, 25, 12, 22, 11 };
    int
                          n = sizeof(arr) / sizeof(arr[0]);
 
    // Function Call
    selectionSort(arr, n);
    cout << "Sorted array: \n";
    printArray(arr, n);
    return 0;
}
 
// This is code is contributed by rathbhupendra

                  

              
            

C

              
                
                    // C program for implementation of selection sort
#include <stdio.h>
                        
 
void swap(int *xp, int *yp)
{
    int
                          temp = *xp;
    *xp = *yp;
    *yp = temp;
}
 
void selectionSort(int arr[], int n)
{
    int
                          i, j, min_idx;
 
    // One by one move boundary of unsorted subarray
    for (i = 0; i < n-1; i++)
    {
        // Find the minimum element in unsorted array
        min_idx = i;
        for (j = i+1; j < n; j++)
          if (arr[j] < arr[min_idx])
            min_idx = j;
 
        // Swap the found minimum element with the first element
           if(min_idx != i)
            swap(&arr[min_idx], &arr[i]);
    }
}
 
/* Function to print an array */
void printArray(int arr[], int size)
{
    int
                          i;
    for (i=0; i < size; i++)
        printf("%d ", arr[i]);
    printf("\n");
}
 
// Driver program to test above functions
int main()
{
    int
                          arr[] = {64, 25, 12, 22, 11};
    int
                          n = sizeof(arr)/sizeof(arr[0]);
    selectionSort(arr, n);
    printf("Sorted array: \n");
    printArray(arr, n);
    return 0;
}

                  

              
            

Python3

              
                    # Python program for implementation of Selection
# Sort
import sys
A = [64, 25, 12, 22, 11]
 
# Traverse through all array elements
for i in range(len(A)):
     
    # Find the minimum element in remaining 
    # unsorted array
    min_idx = i
                        
    for
                          j in range(i+1, len(A)):
        if A[min_idx] > A[j]:
            min_idx = j
                        
    # Swap the found minimum element with 
    # the first element        
    A[i], A[min_idx] = A[min_idx], A[i]
 
# Driver code to test above
print ("Sorted array")
                        
for i in range(len(A)):
    print("%d"
                          %A[i],end=" , ")

Java

              
                
                    // Java program for implementation of Selection Sort
import java.io.*;
public class SelectionSort
{
    void
                          sort(int arr[])
    {
        int n = arr.length;
 
        // One by one move boundary of unsorted subarray
        for (int
                          i = 0; i < n-1; i++)
        {
            // Find the minimum element in unsorted array
            int min_idx = i;
            for (int
                          j = i+1; j < n; j++)
                if (arr[j] < arr[min_idx])
                    min_idx = j;
 
            // Swap the found minimum element with the first
            // element
            int temp = arr[min_idx];
            arr[min_idx] = arr[i];
            arr[i] = temp;
        }
    }
 
    // Prints the array
    void
                          printArray(int arr[])
    {
        int n = arr.length;
        for (int
                          i=0; i<n; ++i)
            System.out.print(arr[i]+" ");
        System.out.println();
    }
 
    // Driver code to test above
    public
                          static void main(String args[])
    {
        SelectionSort ob = new SelectionSort();
        int arr[] = {64,25,12,22,11};
        ob.sort(arr);
        System.out.println("Sorted array");
        ob.printArray(arr);
    }
}
/* This code is contributed by Rajat Mishra*/

                  

              
            

C＃

              
                
                    // C# program for implementation 
// of Selection Sort
using System;
 
class GFG
{ 
    static
                          void sort(int []arr)
    {
        int n = arr.Length;
 
        // One by one move boundary of unsorted subarray
        for (int
                          i = 0; i < n - 1; i++)
        {
            // Find the minimum element in unsorted array
            int min_idx = i;
            for (int
                          j = i + 1; j < n; j++)
                if (arr[j] < arr[min_idx])
                    min_idx = j;
 
            // Swap the found minimum element with the first
            // element
            int temp = arr[min_idx];
            arr[min_idx] = arr[i];
            arr[i] = temp;
        }
    }
 
    // Prints the array
    static
                          void printArray(int []arr)
    {
        int n = arr.Length;
        for (int
                          i=0; i<n; ++i)
            Console.Write(arr[i]+" ");
        Console.WriteLine();
    }
 
    // Driver code 
    public
                          static void Main()
    {
        int []arr = {64,25,12,22,11};
        sort(arr);
        Console.WriteLine("Sorted array");
        printArray(arr);
    }
 
}
// This code is contributed by Sam007

                  

              
            

PHP

              
                
                    <?php
// PHP program for implementation 
// of selection sort 
function selection_sort(&$arr, $n) 
{
    for($i = 0; $i < $n ; $i++)
    {
        $low = $i;
        for($j = $i + 1; $j < $n ; $j++)
        {
            if ($arr[$j] < $arr[$low])
            {
                $low = $j;
            }
        }
         
        // swap the minimum value to $ith node
        if ($arr[$i] > $arr[$low])
        {
            $tmp = $arr[$i];
            $arr[$i] = $arr[$low];
            $arr[$low] = $tmp;
        }
    }
}
 
// Driver Code
$arr = array(64, 25, 12, 22, 11);
$len = count($arr);
selection_sort($arr, $len);
echo "Sorted array : \n"; 
 
for ($i = 0; $i < $len; $i++) 
    echo
                          $arr[$i] . " "; 
 
// This code is contributed 
// by Deepika Gupta. 
                        
?> 

                  

              
            

JavaScript

              
                
                    <script>
// Javascript program for implementation of selection sort
function swap(arr,xp, yp)
{
    var
                          temp = arr[xp];
    arr[xp] = arr[yp];
    arr[yp] = temp;
}
 
function selectionSort(arr,  n)
{
    var
                          i, j, min_idx;
 
    // One by one move boundary of unsorted subarray
    for
                          (i = 0; i < n-1; i++)
    {
        // Find the minimum element in unsorted array
        min_idx = i;
        for (j = i + 1; j < n; j++)
        if (arr[j] < arr[min_idx])
            min_idx = j;
 
        // Swap the found minimum element with the first element
        swap(arr,min_idx, i);
    }
}
 
function printArray( arr,  size)
{
    var
                          i;
    for
                          (i = 0; i < size; i++)
        document.write(arr[i] + " ");
    document.write(" <br>");
}
 
var arr = [64, 25, 12, 22, 11];
    var
                          n = 5;
    selectionSort(arr, n);
    document.write("Sorted array: <br>");
    printArray(arr, n);
 
// This code is contributed by akshitsaxenaa09.
</script>

                  

              
            

输出

排序数组：
11 12 22 25 64

选择排序的复杂度分析

时间复杂度： 选择排序的时间复杂度为 O(N ² ) ，因为有两个嵌套循环：

一个循环逐一选择 Array 的元素 = O(N)
另一个循环将该元素与每个其他数组元素进行比较 = O(N)
因此总体复杂度 = O(N) * O(N) = O(N*N) = O(N ² )

辅助空间： O(1)，因为在交换数组中的两个值时，唯一使用的额外内存用于临时变量。选择排序不会进行超过 O(N) 的交换，并且在内存写入成本高昂时非常有用。

选择排序算法的优点

简单易懂。
适用于小型数据集。

选择排序算法的缺点

在最坏和平均情况下，选择排序的时间复杂度为 O(n^2)。
在大型数据集上效果不佳。
不保留具有相同键的项目的相对顺序，这意味着它不稳定。

选择排序的常见问题

Q1. 选择排序算法稳定吗？

选择排序算法的默认实现并不稳定。然而，它可以变得稳定。详细信息请参阅稳定的选择排序。

Q2。选择排序算法是否到位？

是的，选择排序算法是一种就地算法，因为它不需要额外的空间。