关键路径可视化交互式动画版

关键路径法（CPM）是项目规划中使用的一种方法，通常用于项目调度以按时完成项目。它有助于确定整个项目的最早完成时间。该方法有两个主要概念，即关键任务和关键路径。

表中的内容

什么是项目管理中的关键任务？
项目管理的关键路径是什么？
在项目管理中使用关键路径法的好处：
如何找到项目中的关键路径：
设计 Activity-on-Node 网络图的规则：
节点表示：
节点上的活动图：
项目管理关键路径中的前向传递：
项目管理关键路径中的向后传递：

什么是项目管理中的关键任务？

这是不能延迟的任务/活动，否则整个项目的完成将被延迟。它必须在开始其他相关任务之前按时完成。

项目管理的关键路径是什么？

它是一系列关键任务/活动，并且是项目网络中最大的路径。它为我们提供了完成整个项目所需的最短时间。关键路径中的活动被称为关键活动，如果这些活动被延迟，那么整个项目的完成也会被延迟。

在项目管理中使用关键路径法的好处：

直观地显示项目进度。
使用 CPM 突出显示重要任务。
使用CPM来发现和处理风险。
CPM 帮助项目团队更好地沟通。

如何找到项目中的关键路径：

步骤 1：确定完成项目所需的所有任务
第 2 步：确定任务顺序
第 3 步：估计每项任务的持续时间
第四步：绘制网络图
第 5 步：确定关键路径
第 6 步：计算浮动
第 7 步：监控关键路径

下表包含活动标签、其各自的持续时间（以周为单位）及其先例。我们将使用关键路径方法来查找该项目的关键路径和活动。

活动	持续时间（以周为单位）	先例
A	6	–
乙	4	–
C	3	A
D	4	乙
乙	3	乙
F	10	–
G	3	乙、氟
H	2	光盘

设计 Activity-on-Node 网络图的规则：

一个项目网络应该只有一个起始节点
一个项目网络应该只有一个终端节点
节点有持续时间
链接通常没有持续时间
“先例”是指紧接在前的活动
时间在项目网络中从左向右移动
网络不应包含环路
网络不应包含悬挂物

节点表示：

活动标签 是该节点所代表的活动的名称。
最早开始 是指活动最早可以开始的日期或时间。
最早完成 是指活动最早可以完成的日期或时间。
最晚开始 是活动最迟可以开始的日期或时间。
最晚完成 是最晚可以完成活动的日期或时间。
浮动时间 等于最早开始和最晚开始或最早结束和最晚结束之间的差。

节点上的活动图：

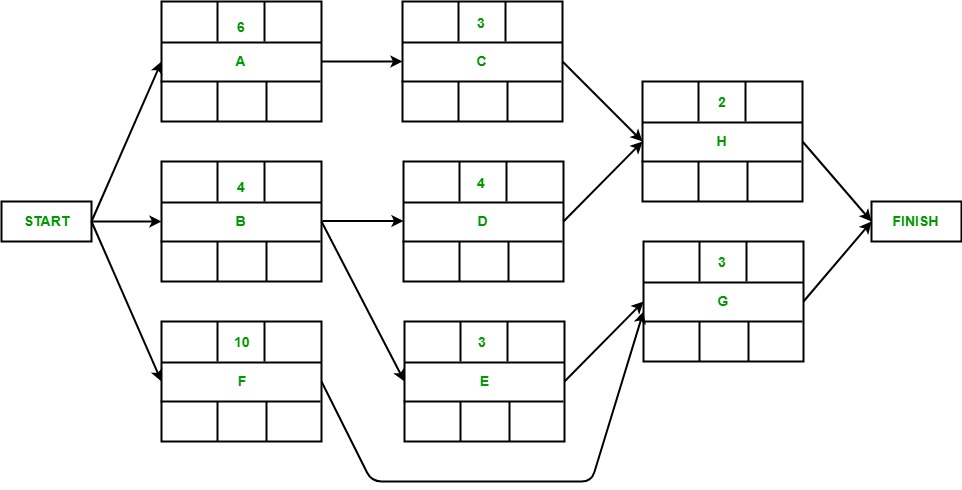
项目管理关键路径中的前向传递：

执行前向传递是为了计算每项活动可以开始和完成的最早日期。

活动 A 可能会立即开始。因此，其最早开始日期为零，即 ES(A) = 0。需要 6 周才能完成执行。因此，最早可以完成是第 6 周，即 EF(A) = 6。
活动 B 可以立即开始。因此，其最早开始日期为零，即 ES(B) = 0。需要 4 周才能完成执行。因此，它最早可以完成是第 4 周，即 EF(B) = 4。
活动 F 可以立即开始。因此，其最早开始日期为零，即 ES(F) = 0。完成执行需要 10 周。因此，它最早可以完成是第 10 周，即 EF(F) = 10。
活动 A 完成执行后，活动 C 就会启动。因此，它最早可以开始执行的周是第 6 周，即 ES(C) = 6。完成执行需要 3 周。因此，它最早可以完成是第 9 周，即 EF(C) = 9。
活动 B 完成执行后，活动 D 立即启动。因此，它最早可以开始执行的周是第 4 周，即 ES(D) = 4。完成执行需要 4 周。因此，它最早可以完成是第 8 周，即 EF(D) = 8。
活动 B 完成执行后，活动 E 立即开始。因此，它最早可以开始执行的周是第 4 周，即 ES(E) = 4。完成执行需要 3 周。因此，它最早可以完成是第 7 周，即 EF(E) = 7。
一旦活动 E 和活动 F 完成执行，活动 G 就会开始。由于该活动需要完成两者才能开始执行，因此我们将考虑 MAX(ES(E), ES(F))。因此，它最早可以开始执行的周是第 10 周，即 ES(G) = 10。完成执行需要 3 周。因此，它最早可以完成是第 13 周，即 EF(G) = 13。
一旦活动 C 和活动 D 完成执行，活动 H 就会开始。由于该活动需要完成两者才能开始执行，因此我们将考虑 MAX(ES(C), ES(D))。因此，它最早可以开始执行的周是第 9 周，即 ES(H) = 9。需要 2 周才能完成执行。因此，它最早可以完成是第 11 周，即 EF(H) = 11。

项目管理关键路径中的向后传递：

进行向后传递是为了计算每项活动可以开始和完成的最晚日期，而不会延迟项目的结束日期。假设：最晚完成日期=（项目）最早完成日期。

根据假设，活动 G 的最晚完成日期等于完成的先行活动的最早完成日期，即 LF(G) = 13。完成其执行需要 3 周。因此，最晚可以开始是第 10 周，即 LS(G) = 10。
根据假设，即 LF(H) = 13，活动 H 的最迟完成日期等于 finish 的前一个活动的最早完成日期。完成其执行需要 2 周。因此，最迟可以开始的是第 11 周，即 LS(H) = 11。
活动 C 的最晚结束日期将是 H 的最晚开始日期，即 LF(C) = 11。完成其执行需要 3 周。因此，最迟可以开始的是第 8 周，即 LS(C) = 8。
活动 D 的最晚结束日期将是 H 的最晚开始日期，即 LF(D) = 11。完成其执行需要 4 周。因此，最迟可以开始的是第 7 周，即 LS(D) = 7。
活动 E 的最晚结束日期将是 G 的最晚开始日期，即 LF(G) = 10。完成其执行需要 3 周。因此，最迟可以开始的是第 7 周，即 LS(E) = 7。
活动 F 的最晚结束日期将是 G 的最晚开始日期，即 LF(G) = 10。完成其执行需要 10 周。因此，最迟可以开始的是第 0 周，即 LS(F) = 0。
活动 A 的最晚结束日期将是 C 的最晚开始日期，即 LF(A) = 8。完成其执行需要 6 周。因此，最晚可以开始是第 2 周，即 LS(A) = 2。
活动 B 的最晚结束日期将是 D 和 E 的最晚开始日期中最早的日期，即 LF(B) = 7。完成其执行需要 4 周。因此，最迟可以开始的是第 3 周，即 LS(B) = 3。

项目管理关键路径中的向后传递

识别关键路径： 关键路径是给我们或帮助我们估计整个项目最早完成时间的路径。这条关键路径上的任何活动的延误都会导致整个项目完成的延误。为了确定关键路径，我们需要计算每个活动的活动浮动时间。活动浮动时间是活动的最早开始日期和最晚开始日期之间的差值，或者活动的最早结束日期和最晚结束日期之间的差值，它表明在不延迟整个项目完成的情况下，活动可以延迟多少。如果活动的浮动为零，则该活动是关键的，必须添加到项目网络的关键路径中。在此示例中，活动 F 和 G 的浮动时间为零，因此是关键活动。