正在载入交互式动画窗口请稍等
希尔排序 可视化交互式动画版

希尔排序主要是 插入排序 的变体 。 在插入排序中,我们仅将元素向前移动一位。 当一个元素必须向前移动很远时,会涉及到许多动作。 ShellSort 的想法是允许交换远距离的项目。 在希尔排序中,我们对 h 值较大的数组进行 h 排序。 我们不断减少 h 的值,直到它变成 1。如果每个第 h 个元素的所有子列表都已排序,则称数组是 h 排序的。
算法:
步骤 1 - 开始
步骤 2 - 初始化间隙大小的值。
示例:h
步骤 3 - 将列表分为更小的子部分。
每个子列表必须与 h 具有相等的间隔
步骤 4 - 使用插入排序对这些子列表进行排序
步骤 5 - 重复此步骤 2,直到列表排序完毕。
第 6 步 – 打印排序列表。
第 7 步 – 停止。
伪代码 :
过程 SHELL_SORT(ARRAY, N)
WHILE GAP < LENGTH(ARRAY) /3 :
GAP =
( INTERVAL * 3 ) + 1
END WHILE 循环
WHILE GAP > 0 :
FOR (OUTER = GAP; OUTER < LENGTH(ARRAY);
OUTER++):
INSERTION_VALUE = 数组[外部]
内部 =
外部;
WHILE INNER > GAP-1 AND
ARRAY[INNER – GAP] >= INSERTION_VALUE:
ARRAY[INNER] = ARRAY[INNER – GAP]
INNER
= INNER – GAP
END WHILE LOOP
ARRAY[INNER]
= INSERTION_VALUE
END FOR LOOP
GAP = (GAP - 1)/3;
END WHILE 循环
结束 SHELL_SORT
下面是ShellSort的实现。
- C++
- Java
- Python3
- C#
- JavaScript
C++
// C++ implementation of Shell Sort #include <iostream> using namespace std; /* function to sort arr using shellSort */int shellSort(int arr[], int n) { // Start with a big gap, then reduce the gap for (int gap = n/2; gap > 0; gap /= 2)
{ // Do a gapped insertion sort for this gap size. // The first gap elements a[0..gap-1] are already in gapped order
// keep adding one more element until the entire array is // gap sorted for (int i = gap; i < n; i += 1) { // add a[i] to the elements that have been gap sorted // save a[i] in temp and make a hole at position i int temp = arr[i]; // shift earlier gap-sorted elements up until the correct
// location for a[i] is found int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) arr[j] = arr[j - gap];
// put temp (the original a[i]) in its correct location arr[j] = temp; } } return 0; } void printArray(int arr[], int n) { for (int i=0; i<n; i++) cout << arr[i] << " "; } int main() { int
arr[] = {12, 34, 54, 2, 3}, i; int
n = sizeof(arr)/sizeof(arr[0]); cout << "Array before sorting: \n"; printArray(arr, n); shellSort(arr, n); cout << "\nArray after sorting: \n"; printArray(arr, n); return 0; } |
Java
Python3
C#
Javascript
排序前的数组: 12 34 54 2 3 排序后的数组: 2 3 12 34 54
时间复杂度: 上述希尔排序实现的时间复杂度为O(n 2 )。 在上面的实现中,每次迭代时间隙都会减少一半。 还有许多其他方法可以减少间隙,从而提高时间复杂度。 请参阅 此 了解更多详细信息。
最坏情况复杂度
希尔排序的最坏情况复杂度为
O(n
2
)
最佳情况复杂度
当给定数组列表已排序时,每个区间的比较总数等于给定数组的大小。
因此,最佳情况复杂度为 Ω(n log(n))
平均情况复杂度
希尔排序的平均情况复杂度取决于程序员选择的区间。
θ(n log(n)2)
。
平均情况复杂度: O(n*log n)~O(n
1.25
)
空间复杂度
希尔排序的空间复杂度为
O(1)
。
问题:
1. 希尔排序和堆排序哪个更高效?
答。
根据大 O 表示法,希尔排序的平均时间复杂度为 O(n^{1.25}),而堆排序的时间复杂度为 O(N log N)。
根据大 O 表示法的严格数学解释,当我们要排序的元素接近 2000 个时,堆排序在效率上超过了希尔排序。
注意:-
Big-O 是舍入近似值,分析评估并不总是 100% 正确,它取决于算法的实现,这可能会影响实际运行时间。
希尔排序应用
1. 替代插入排序,它需要很长时间才能完成给定的任务。
2. 为了调用堆栈开销,我们使用希尔排序。
3.当递归超过特定限制时,我们使用希尔排序。
4. 对于中型到大型数据集。
5.减少插入排序中的操作次数。
参考文献: http:
//en.wikipedia.org/wiki/Shellsort
快照:

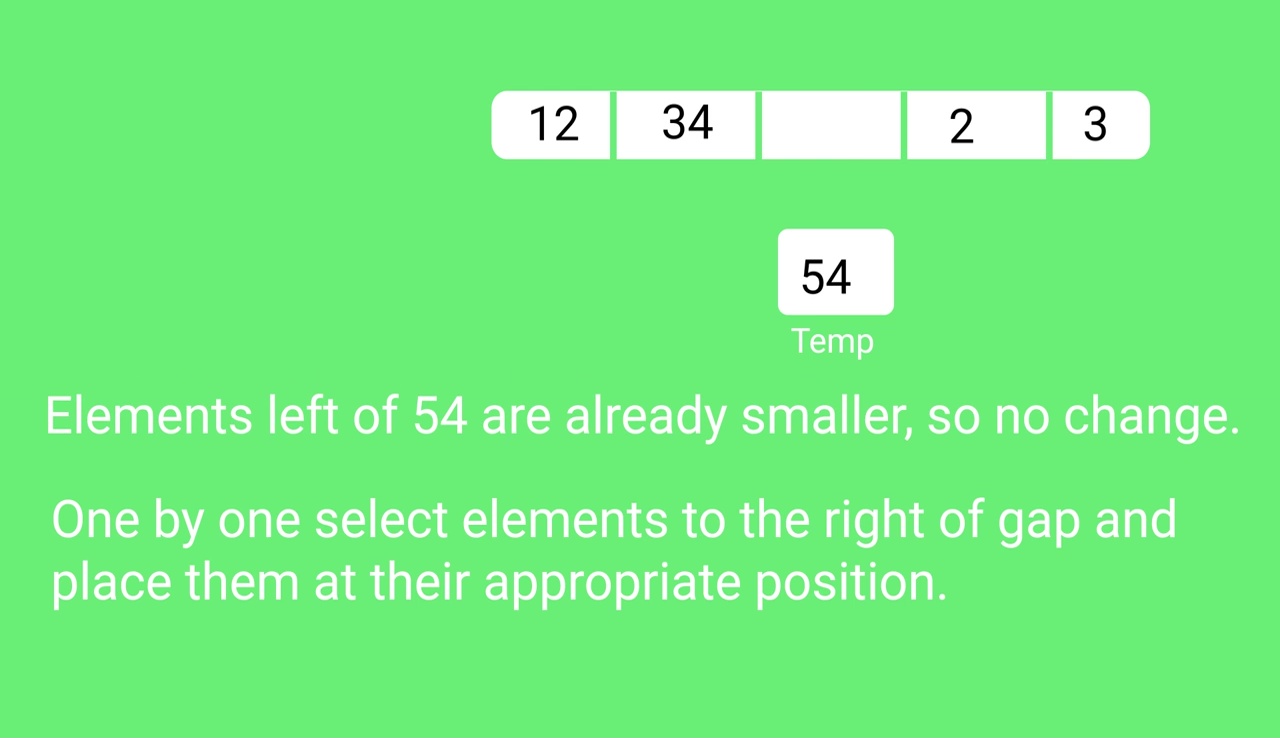




希尔排序测验
图码/GeeksQuiz 上的其他排序算法:
- 选择排序
- 冒泡排序
- 插入排序
- 归并排序
- 堆排序
- 快速排序
- 排序基数
- 计数排序
- 桶排序