正在载入交互式动画窗口请稍等
存储结构-邻接矩阵 可视化交互式动画版

邻接矩阵 是 N x N 大小的方阵,其中 N 是图中的节点数,用于表示图的边之间的连接。
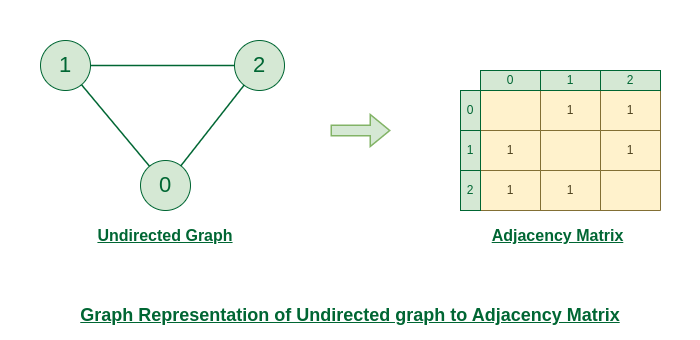
无向图到邻接矩阵的图表示
邻接矩阵的特点是:
- 矩阵的大小由图中的顶点数决定。
- 图中的节点数量决定了矩阵的大小。
- 简单计算图中的边数。
- 如果图的边很少,则矩阵将是稀疏的。
如何构建邻接矩阵:
为图构建邻接矩阵非常容易和简单,您需要遵循下面给出的某些步骤:
- 创建一个 nxn 矩阵,其中 n 是图中的顶点数。
- 将所有元素初始化为 0。
- 对于图中的每条边 (u, v),如果图是无向的,则将 a[u][v] 和 a[v][u] 标记为 1,如果边从 u 指向 v , 则将 a [ u][v] 为 1。(如果图形已加权,则单元格将填充边权重)
邻接矩阵的应用:
- 图算法: 许多图算法(例如 Dijkstra 算法 、 Floyd-Warshall 算法 和 Kruskal 算法) 都使用邻接矩阵来表示图。
- 图像处理 : 图像处理中使用邻接矩阵来表示图像中像素之间的邻接关系。
- 寻找两个节点之间的最短路径: 通过对邻接矩阵进行矩阵乘法,可以找到图中任意两个节点之间的最短路径。
使用邻接矩阵的优点:
- 邻接矩阵简单且易于理解。
- 在图表中添加或删除边既快速又简单。
- 它允许恒定时间访问图中的任何边。
使用邻接矩阵的缺点:
- 对于稀疏图来说,它的空间利用率很低,因为它占用了 O(N 2 ) 空间。
- 计算一个顶点的所有邻居需要 O(N) 时间。
你还能读什么?
- Kruskal 算法(邻接矩阵的简单实现)
- 将邻接矩阵转换为图的邻接列表表示
- 将邻接列表转换为图的邻接矩阵表示
- 图的邻接表与邻接矩阵表示的比较