存储结构-邻接链表可视化交互式动画版

邻接列表是一种用于表示图的数据结构，其中图中的每个节点都存储其相邻顶点的列表。

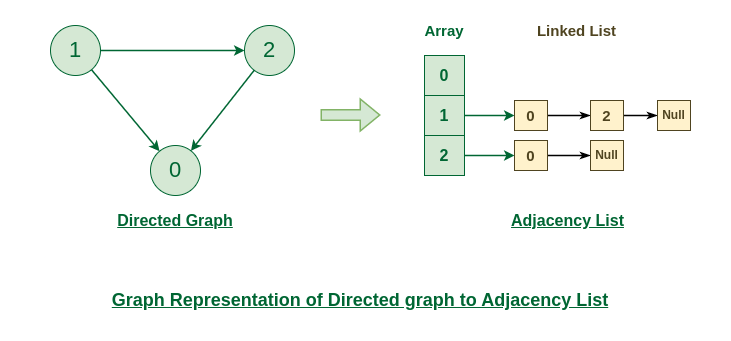
有向图到邻接表的图表示

邻接表的特点：

矩阵的大小由网络中节点的数量决定。
图边的数量很容易计算。
邻接表是一个 锯齿状数组 。

如何建立邻接表？

为图构建邻接表非常容易和简单，您需要遵循下面给出的某些步骤：

创建大小为N 的链表数组，其中 N 是图中的顶点数。
为图中的每个顶点创建相邻顶点的链表。
对于图中的每条边 (u, v) ，将 v添加到 u 的链表中，如果图是无向的，则将 u添加到 v 的链表中，否则如果从 u 有向，则将 v添加到 u 的链表中 v . （如果是加权图，则将权重与连接一起存储）。

邻接表的应用：

图算法：许多图算法（例如 Dijkstra 算法、广度优先搜索和深度优先搜索）使用邻接表来表示图。
图像处理：邻接列表可用于表示图像中像素之间的邻接关系。
游戏开发：这些列表可用于存储有关不同区域或级别之间连接的信息，游戏开发人员使用图形来表示游戏地图或级别。

使用邻接表的优点：

邻接表简单且易于理解。
在图表中添加或删除边既快速又简单。

使用邻接表的缺点：

在邻接列表中，访问边可能比邻接矩阵花费更长的时间。
对于稠密图，它比邻接矩阵需要更多的内存。

你还能读什么？

DSA中邻接矩阵的含义和定义
在图的邻接列表表示中添加和删除边
将邻接矩阵转换为图的邻接列表表示
将邻接列表转换为图的邻接矩阵表示
图的邻接表与邻接矩阵表示的比较

广度 优先搜索 (BFS) 算法用于在图数据结构中搜索满足一组条件的节点。它从图的根开始，访问当前深度级别的所有节点，然后再移动到下一个深度级别的节点。

图遍历和树遍历的BFS之间的关系：

图的广度优先遍历（或搜索）类似于树的广度优先遍历。

这里唯一的问题是，与树不同，图可能包含循环，因此我们可能会再次到达同一个节点。为了避免多次处理一个节点，我们将顶点分为两类：

参观并
没有访问过。

布尔访问数组用于标记访问过的顶点。为了简单起见，假设所有顶点都可以从起始顶点到达。 BFS使用 队列数据结构 进行遍历。

BFS 是如何工作的？

从根开始，先访问某一层的所有节点，然后遍历下一层的节点，直到访问完所有节点。

为此，使用队列。当前级别的所有相邻未访问节点都被推入队列，当前级别的节点被标记为已访问并从队列中弹出。

插图：

让我们借助以下示例来了解该算法的工作原理。

步骤1： 最初队列和访问数组都是空的。

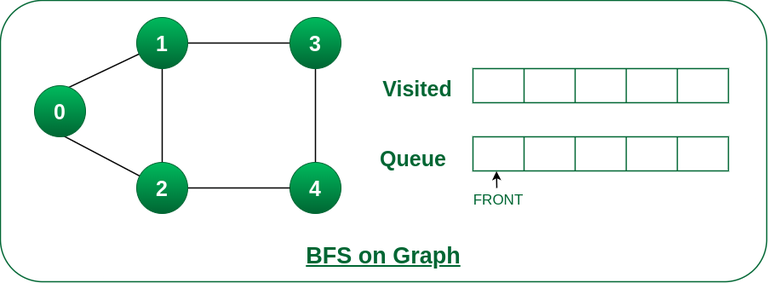
队列和访问数组最初是空的。

步骤2： 将节点0推入队列并标记为已访问。

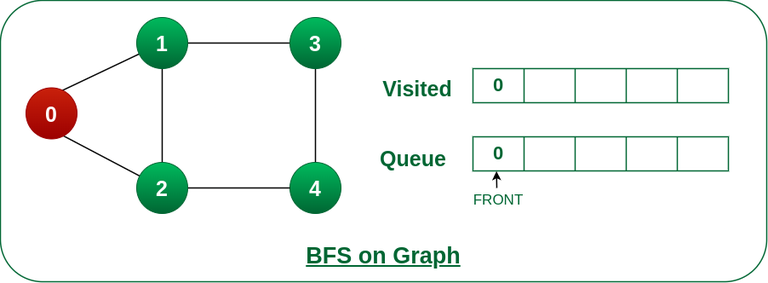
将节点 0 推入队列并将其标记为已访问。

步骤3： 将节点0从队列的前面移除，并访问未访问的邻居并将它们推入队列。

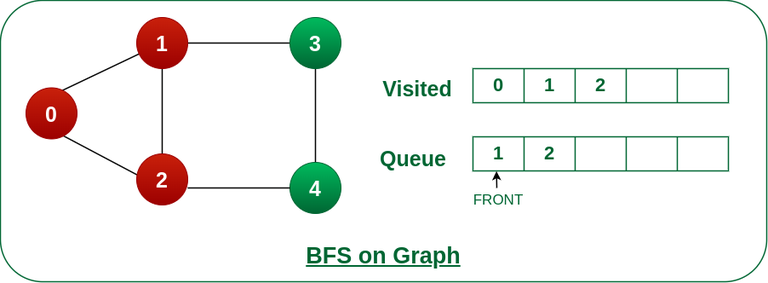
从队列前面删除节点 0 并访问未访问的邻居并推入队列。

步骤4： 将节点1从队列的前面移除，并访问未访问的邻居并将它们推入队列。

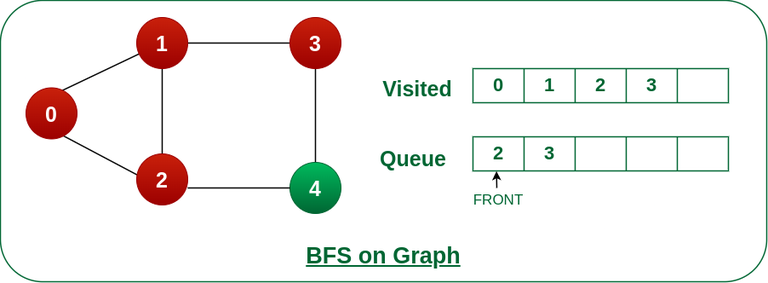
从队列前面删除节点 1 并访问未访问的邻居并推送

步骤5： 将节点2从队列的前面移除，并访问未访问的邻居并将它们推入队列。

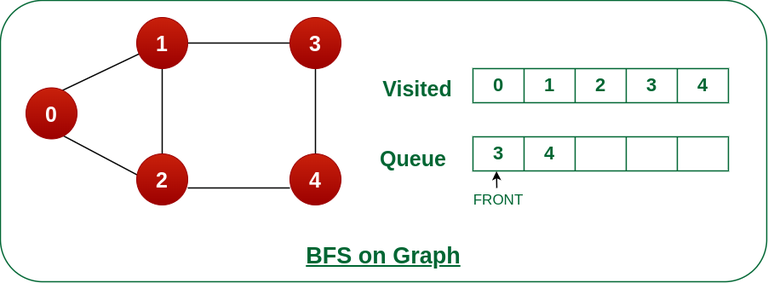
将节点 2 从队列前面移除，并访问未访问的邻居并将它们推入队列。

步骤6： 将节点3从队列的前面移除，并访问未访问的邻居并将它们推入队列。
我们可以看到节点 3 的每个邻居都被访问，因此移动到队列前面的下一个节点。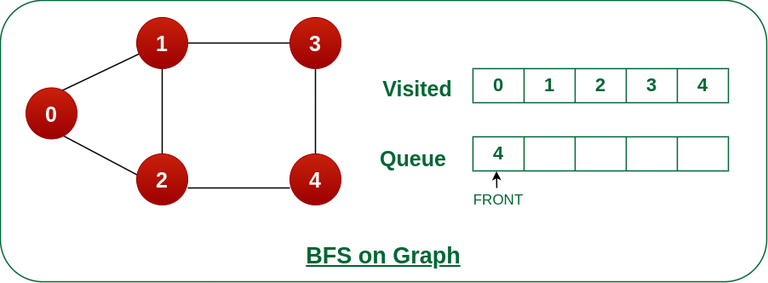

将节点 3 从队列前面移除，并访问未访问的邻居并将它们推入队列。

步骤7： 将节点4从队列的前面移除，并访问未访问的邻居并将它们推入队列。
我们可以看到节点 4 的每个邻居都被访问，因此移动到队列前面的下一个节点。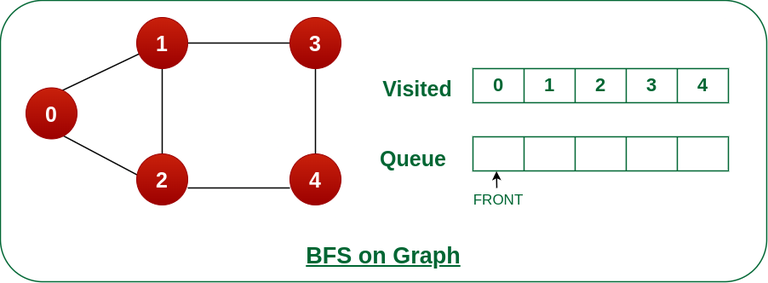

将节点 4 从队列前面移除，并访问未访问的邻居并将它们推入队列。

现在，Queue 变空了，所以，终止这些迭代过程。

使用邻接表实现图的 BFS：

C

              
                
                    #include <stdbool.h>
#include <stdio.h>
                        
#include <stdlib.h>
 
#define MAX_VERTICES 50
                        
 
// This struct represents a directed graph using
// adjacency list representation
typedef struct Graph_t {
 
    // No. of vertices
    int
                          V;
    bool adj[MAX_VERTICES][MAX_VERTICES];
                        
} Graph;
 
// Constructor
Graph* Graph_create(int V)
{
    Graph* g = malloc(sizeof(Graph));
    g->V = V;
 
    for (int i = 0; i < V; i++) {
        for (int j = 0; j < V; j++) {
            g->adj[i][j] = false;
        }
    }
 
    return g;
}
 
// Destructor
void Graph_destroy(Graph* g) { free(g); }
 
// Function to add an edge to graph
void Graph_addEdge(Graph* g, int v, int w)
                        
{
    // Add w to v’s list.
    g->adj[v][w] = true;
}
 
// Prints BFS traversal from a given source s
void Graph_BFS(Graph* g, int s)
{
    // Mark all the vertices as not visited
    bool visited[MAX_VERTICES];
    for (int i = 0; i < g->V; i++) {
                        
        visited[i] = false;
    }
 
    // Create a queue for BFS
    int
                          queue[MAX_VERTICES];
    int
                          front = 0, rear = 0;
 
    // Mark the current node as visited and enqueue it
    visited[s] = true;
    queue[rear++] = s;
 
    while (front != rear) {
 
        // Dequeue a vertex from queue and print it
        s = queue[front++];
        printf("%d ", s);
 
        // Get all adjacent vertices of the dequeued
        // vertex s.
        // If an adjacent has not been visited,
        // then mark it visited and enqueue it
        for (int adjacent = 0; adjacent < g->V;
             adjacent++) {
            if (g->adj[s][adjacent] && !visited[adjacent]) {
                visited[adjacent] = true;
                queue[rear++] = adjacent;
            }
        }
    }
}
 
// Driver code
int main()
{
    // Create a graph
    Graph* g = Graph_create(4);
    Graph_addEdge(g, 0, 1);
    Graph_addEdge(g, 0, 2);
    Graph_addEdge(g, 1, 2);
    Graph_addEdge(g, 2, 0);
    Graph_addEdge(g, 2, 3);
    Graph_addEdge(g, 3, 3);
 
    printf("Following is Breadth First Traversal "
           "(starting from vertex 2) \n");
    Graph_BFS(g, 2);
    Graph_destroy(g);
 
    return 0;
}

                  

              
            

C++

              
                
                    // C++ code to print BFS traversal from a given
// source vertex
 
#include <bits/stdc++.h>
using namespace std;
 
// This class represents a directed graph using
// adjacency list representation
class Graph {
 
    // No. of vertices
    int
                          V;
 
    // Pointer to an array containing adjacency lists
    vector<list<int> > adj;
 
public:
    // Constructor
    Graph(int V);
 
    // Function to add an edge to graph
    void addEdge(int v, int w);
 
    // Prints BFS traversal from a given source s
    void BFS(int s);
};
 
Graph::Graph(int V)
{
    this->V = V;
    adj.resize(V);
}
 
void Graph::addEdge(int v, int w)
                        
{
    // Add w to v’s list.
    adj[v].push_back(w);
}
 
void Graph::BFS(int s)
{
    // Mark all the vertices as not visited
    vector<bool> visited;
    visited.resize(V, false);
 
    // Create a queue for BFS
    list<int> queue;
 
    // Mark the current node as visited and enqueue it
    visited[s] = true;
    queue.push_back(s);
 
    while (!queue.empty()) {
 
        // Dequeue a vertex from queue and print it
        s = queue.front();
        cout << s << " ";
        queue.pop_front();
 
        // Get all adjacent vertices of the dequeued
        // vertex s.
        // If an adjacent has not been visited,
        // then mark it visited and enqueue it
        for (auto adjacent : adj[s]) {
            if (!visited[adjacent]) {
                visited[adjacent] = true;
                queue.push_back(adjacent);
            }
        }
    }
}
 
// Driver code
int main()
{
    // Create a graph given in the above diagram
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);
 
    cout << "Following is Breadth First Traversal "
         << "(starting from vertex 2) \n";
    g.BFS(2);
                        
 
    return 0;
}

                  

              
            

Java

              
                
                    // Java program to print BFS traversal from a given source
// vertex. BFS(int s) traverses vertices reachable from s.
 
import java.io.*;
import java.util.*;
 
// This class represents a directed graph using adjacency
// list representation
class Graph {
 
    // No. of vertices
    private
                          int V;
 
    // Adjacency Lists
    private
                          LinkedList<Integer> adj[];
 
    // Constructor
    Graph(int v)
                        
    {
        V = v;
        adj = new LinkedList[v];
        for (int
                          i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }
 
    // Function to add an edge into the graph
    void
                          addEdge(int v, int w) { adj[v].add(w); }
 
    // prints BFS traversal from a given source s
    void
                          BFS(int s)
                        
    {
        // Mark all the vertices as not visited(By default
        // set as false)
        boolean visited[] = new boolean[V];
 
        // Create a queue for BFS
        LinkedList<Integer> queue
            = new LinkedList<Integer>();
 
        // Mark the current node as visited and enqueue it
        visited[s] = true;
        queue.add(s);
 
        while (queue.size() != 0) {
 
            // Dequeue a vertex from queue and print it
            s = queue.poll();
            System.out.print(s + " ");
 
            // Get all adjacent vertices of the dequeued
            // vertex s.
            // If an adjacent has not been visited,
            // then mark it visited and enqueue it
            Iterator<Integer> i = adj[s].listIterator();
            while (i.hasNext()) {
                int n = i.next();
                if (!visited[n]) {
                    visited[n] = true;
                    queue.add(n);
                }
            }
        }
    }
 
    // Driver code
    public
                          static void main(String args[])
    {
        Graph g = new Graph(4);
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);
 
        System.out.println(
            "Following is Breadth First Traversal "
            + "(starting from vertex 2)");
 
        g.BFS(2);
    }
}
 
// This code is contributed by Aakash Hasija

                  

              
            

Python3

              
                
                    # Python3 Program to print BFS traversal
# from a given source vertex. BFS(int s)
# traverses vertices reachable from s.
 
from collections import defaultdict
 
 
# This class represents a directed graph
# using adjacency list representation
class Graph:
 
    # Constructor
    def
                          __init__(self):
 
        # Default dictionary to store graph
        self.graph =
                          defaultdict(list)
 
    # Function to add an edge to graph
    def
                          addEdge(self, u, v):
        self.graph[u].append(v)
 
    # Function to print a BFS of graph
    def
                          BFS(self, s):
 
        # Mark all the vertices as not visited
        visited = [False] * (max(self.graph) + 1)
 
        # Create a queue for BFS
        queue = []
                        
 
        # Mark the source node as
        # visited and enqueue it
        queue.append(s)
        visited[s] = True
 
        while queue:
 
            # Dequeue a vertex from
            # queue and print it
            s = queue.pop(0)
                        
            print(s, end=" ")
 
            # Get all adjacent vertices of the
            # dequeued vertex s.
            # If an adjacent has not been visited,
            # then mark it visited and enqueue it
            for i in
                          self.graph[s]:
                if visited[i] == False:
                    queue.append(i)
                    visited[i] = True
 
 
# Driver code
if __name__ ==
                          '__main__':
 
    # Create a graph given in
    # the above diagram
    g = Graph()
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(2, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 3)
 
    print("Following is Breadth First Traversal"
          " (starting from vertex 2)")
    g.BFS(2)
 
# This code is contributed by Neelam Yadav

                  

              
            

C#

              
                
                    // C# program to print BFS traversal from a given source
// vertex. BFS(int s) traverses vertices reachable from s.
 
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
 
// This class represents a directed graph
// using adjacency list representation
class Graph {
 
    // No. of vertices
    private
                          int _V;
 
    // Adjacency Lists
    LinkedList<int>[] _adj;
 
    public
                          Graph(int V)
    {
        _adj = new LinkedList<int>[ V ];
        for (int
                          i = 0; i < _adj.Length; i++) {
            _adj[i] = new LinkedList<int>();
        }
        _V = V;
    }
 
    // Function to add an edge into the graph
    public
                          void AddEdge(int v, int
                          w)
    {
        _adj[v].AddLast(w);
    }
 
    // Prints BFS traversal from a given source s
    public
                          void BFS(int s)
    {
 
        // Mark all the vertices as not
        // visited(By default set as false)
        bool[] visited = new bool[_V];
                        
        for (int
                          i = 0; i < _V; i++)
            visited[i] = false;
 
        // Create a queue for BFS
        LinkedList<int> queue = new LinkedList<int>();
 
        // Mark the current node as
        // visited and enqueue it
        visited[s] = true;
        queue.AddLast(s);
 
        while (queue.Any()) {
 
            // Dequeue a vertex from queue
            // and print it
            s = queue.First();
            Console.Write(s + " ");
            queue.RemoveFirst();
 
            // Get all adjacent vertices of the
            // dequeued vertex s.
            // If an adjacent has not been visited,
            // then mark it visited and enqueue it
            LinkedList<int> list = _adj[s];
 
            foreach(var
                          val in list)
            {
                if (!visited[val]) {
                    visited[val] = true;
                    queue.AddLast(val);
                }
            }
        }
    }
 
    // Driver code
    static
                          void Main(string[] args)
    {
        Graph g = new Graph(4);
        g.AddEdge(0, 1);
        g.AddEdge(0, 2);
        g.AddEdge(1, 2);
        g.AddEdge(2, 0);
        g.AddEdge(2, 3);
        g.AddEdge(3, 3);
 
        Console.Write("Following is Breadth First "
                        
                      + "Traversal(starting from "
                      + "vertex 2) \n");
        g.BFS(2);
    }
}
 
// This code is contributed by anv89

                  

              
            

Javascript

              
                
                    // Javacript Program to print BFS traversal from a given
// source vertex. BFS(int s) traverses vertices
// reachable from s.
     
     
// This class represents a directed graph using
// adjacency list representation
class Graph
{
    // Constructor
    constructor(v)
    {
        this.V = v;
        this.adj = new Array(v);
        for(let i = 0; i < v; i++)
            this.adj[i] = [];
    }
         
    // Function to add an edge into the graph
    addEdge(v, w)
    {
        // Add w to v's list.
        this.adj[v].push(w);
    }
         
    // Prints BFS traversal from a given source s
    BFS(s)
                        
    {
        // Mark all the vertices as not visited(By default
        // set as false)
        let visited = new Array(this.V);
                        
        for(let i = 0; i < this.V; i++)
            visited[i] = false;
             
                        
        // Create a queue for BFS
        let queue=[];
             
                        
        // Mark the current node as visited and enqueue it
        visited[s]=true;
        queue.push(s);
             
                        
        while(queue.length>0)
        {
            // Dequeue a vertex from queue and print it
            s = queue[0];
            console.log(s+" ");
            queue.shift();
                 
                        
            // Get all adjacent vertices of the dequeued
            // vertex s. 
            // If an adjacent has not been visited,
            // then mark it visited and enqueue it
            this.adj[s].forEach((adjacent,i) => { 
                        
                if(!visited[adjacent])
                {
                    visited[adjacent]=true;
                    queue.push(adjacent);
                }
            });
        }
    }
}
     
// Driver program to test methods of graph class
     
    // Create a graph given in the above diagram
    g = new Graph(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);
     
    console.log("Following is Breadth First Traversal " +
                        
                "(starting from vertex 2) ");
     
    g.BFS(2);
                        
     
// This code is contributed by Aman Kumar.

                  

              
            

输出

以下是广度优先遍历（从顶点2开始）
2 0 3 1

时间复杂度： O(V+E)，其中V是节点数，E是边数。
辅助空间： O(V)

BFS相关问题：

编号	问题	实践
1.	查找无向图中给定节点的级别	关联
2.	最小化从左上角到右下角的路径中的最大相邻差异	关联
3.	最小跳转到相同值或相邻值以到达数组末尾	关联
4.	通过跳过矩阵中路径上的 K 个障碍，在最短的时间内获得最多的硬币	关联
5.	检查是否可以从给定节点访问无向图的所有节点	关联
6.	至少访问给定图的所有节点一次的最短时间	关联
7.	最小化移动到下一个更大的元素以到达数组的末尾	关联
8.	移除 K 堵墙的最短路径	关联
9.	感染二叉树所有节点所需的最短时间	关联
10.	检查给定矩阵的目标是否可以通过所需的单元值到达	关联

你还可以读什么？

关于 BFS 的最新文章
深度优先遍历
广度优先遍历的应用
深度优先搜索的应用

如果您发现任何不正确的内容，或者您想分享有关上述主题的更多信息，请发表评论。

图的深度优先遍历（或 DFS） 类似于树的深度优先遍历。这里唯一的问题是，与树不同，图可能包含循环（一个节点可能被访问两次）。为了避免多次处理节点，请使用布尔访问数组。一张图可以有多个 DFS 遍历。

例子：

输入： n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3 输出：来自顶点 1 的
DFS : 1 2 0 3
解释：
DFS图：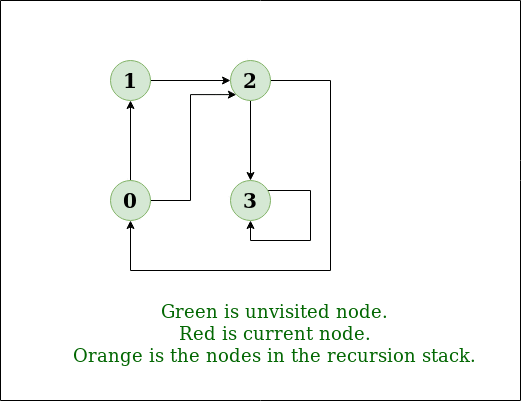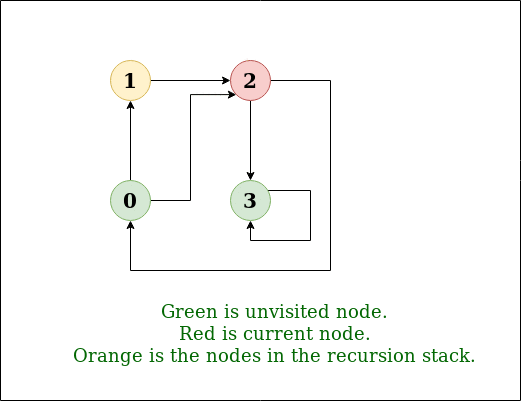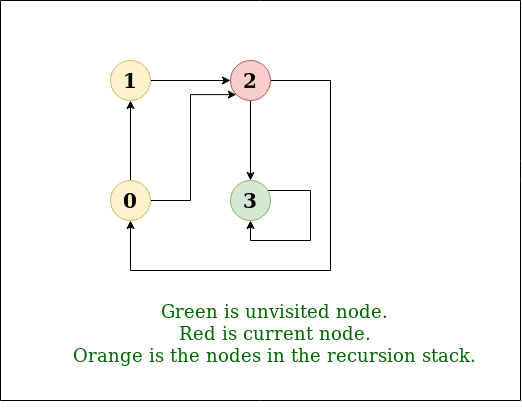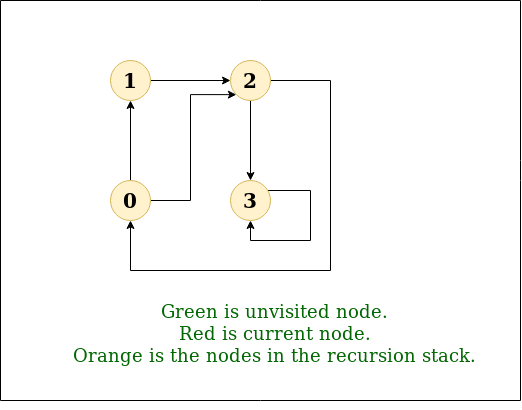

实施例1

输入： n = 4, e = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3 输出：来自
顶点 2 的 DFS : 2 0 1 3
解释：
DFS图：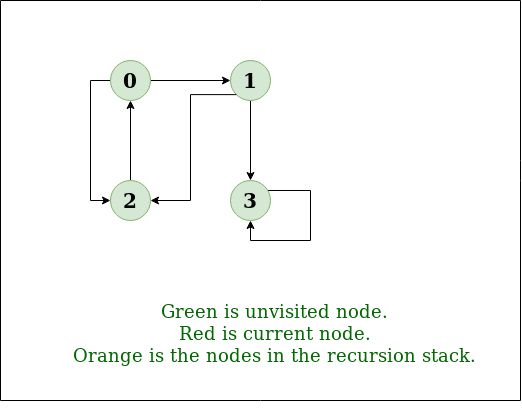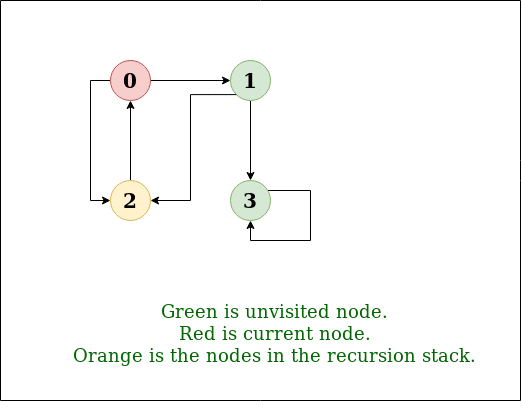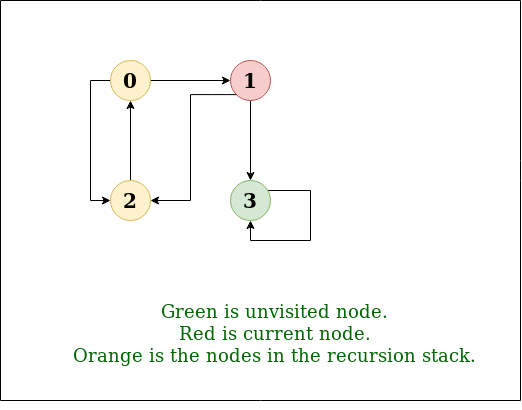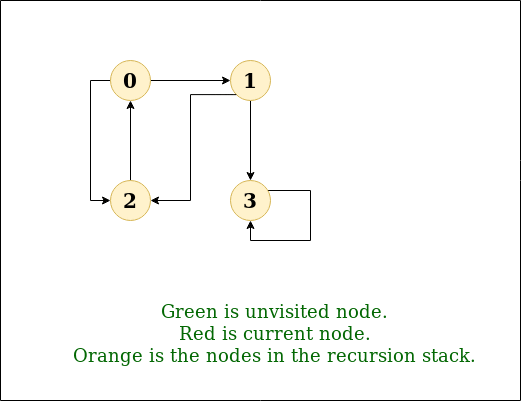

实施例2

DFS 是如何工作的？

深度优先搜索是一种用于遍历或搜索树或图数据结构的算法。该算法从根节点开始（在图的情况下选择某个任意节点作为根节点），并在回溯之前沿着每个分支尽可能远地探索。

让我们借助下图来了解 深度优先搜索 的工作原理：

步骤1： 最初堆栈和访问数组都是空的。

步骤2： 访问0，将其未访问过的相邻节点放入栈中。

访问节点0并将其相邻节点(1,2,3)放入堆栈

步骤3： 现在，节点1位于栈顶，因此访问节点1并将其从栈中弹出，并将其所有未访问的相邻节点放入栈中。

访问节点1

步骤4： 现在，节点2位于栈顶，因此访问节点2并将其从栈中弹出，并将其所有未访问的相邻节点（即3、4）放入栈中。

访问节点2并将其未访问的相邻节点(3, 4)放入堆栈

步骤5： 现在，节点4位于栈顶，因此访问节点4并将其从栈中弹出，并将其所有未访问的相邻节点放入栈中。

访问节点4

步骤6： 现在，节点3位于栈顶，因此访问节点3并将其从栈中弹出，并将其所有未访问的相邻节点放入栈中。

访问节点3

现在，Stack 变空了，这意味着我们已经访问了所有节点，我们的 DFS 遍历结束了。

下面是上述方法的实现：

C++
Java
Python3
C＃
JavaScript

C++

              
                
                    // C++ program to print DFS traversal from
// a given vertex in a  given graph
#include <bits/stdc++.h>
using namespace std;
 
// Graph class represents a directed graph
// using adjacency list representation
class Graph {
public:
    map<int, bool> visited;
    map<int, list<int> > adj;
 
    // Function to add an edge to graph
    void addEdge(int v, int w);
 
    // DFS traversal of the vertices
    // reachable from v
    void DFS(int v);
};
 
void Graph::addEdge(int v, int w)
                        
{
    // Add w to v’s list.
    adj[v].push_back(w);
}
 
void Graph::DFS(int v)
{
    // Mark the current node as visited and
    // print it
    visited[v] = true;
    cout << v << " ";
 
    // Recur for all the vertices adjacent
    // to this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFS(*i);
}
 
// Driver code
int main()
{
    // Create a graph given in the above diagram
    Graph g;
                        
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);
 
    cout << "Following is Depth First Traversal"
            " (starting from vertex 2) \n";
 
    // Function call
    g.DFS(2);
                        
 
    return 0;
}
 
// improved by Vishnudev C
                        

                  

              
            

Java

              
                
                    // Java program to print DFS traversal
// from a given graph
import java.io.*;
import java.util.*;
 
// This class represents a
                        
// directed graph using adjacency
// list representation
class Graph {
    private
                          int V;
 
    // Array  of lists for
    // Adjacency List Representation
    private
                          LinkedList<Integer> adj[];
 
    // Constructor
    @SuppressWarnings("unchecked") Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int
                          i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }
 
    // Function to add an edge into the graph
    void
                          addEdge(int v, int w)
    {
        // Add w to v's list.
        adj[v].add(w);
    }
 
    // A function used by DFS
    void
                          DFSUtil(int v, boolean visited[])
    {
        // Mark the current node as visited and print it
        visited[v] = true;
        System.out.print(v + " ");
 
        // Recur for all the vertices adjacent to this
        // vertex
        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }
 
    // The function to do DFS traversal.
    // It uses recursive DFSUtil()
    void
                          DFS(int v)
                        
    {
        // Mark all the vertices as
        // not visited(set as
        // false by default in java)
        boolean visited[] = new boolean[V];
 
        // Call the recursive helper
        // function to print DFS
        // traversal
        DFSUtil(v, visited);
    }
 
    // Driver Code
    public
                          static void main(String args[])
    {
        Graph g = new Graph(4);
 
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);
 
        System.out.println(
            "Following is Depth First Traversal "
            + "(starting from vertex 2)");
 
        // Function call
        g.DFS(2);
    }
}
// This code is contributed by Aakash Hasija

                  

              
            

Python3

              
                
                    # Python3 program to print DFS traversal
# from a given  graph
                        
from collections import defaultdict
 
 
# This class represents a directed graph using
# adjacency list representation
class Graph:
 
    # Constructor
    def
                          __init__(self):
 
        # Default dictionary to store graph
        self.graph =
                          defaultdict(list)
 
     
    # Function to add an edge to graph
    def
                          addEdge(self, u, v):
        self.graph[u].append(v)
 
     
    # A function used by DFS
    def
                          DFSUtil(self, v, visited):
 
        # Mark the current node as visited
        # and print it
        visited.add(v)
        print(v, end=' ')
 
        # Recur for all the vertices
        # adjacent to this vertex
        for neighbour in self.graph[v]:
            if neighbour not in visited:
                self.DFSUtil(neighbour, visited)
 
     
    # The function to do DFS traversal. It uses
    # recursive DFSUtil()
    def
                          DFS(self, v):
 
        # Create a set to store visited vertices
        visited = set()
 
        # Call the recursive helper function
        # to print DFS traversal
        self.DFSUtil(v, visited)
 
 
# Driver's code
if __name__ ==
                          "__main__":
    g = Graph()
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(2, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 3)
 
    print("Following is Depth First Traversal (starting from vertex 2)")
     
    # Function call
    g.DFS(2)
 
# This code is contributed by Neelam Yadav

                  

              
            

C＃

              
                
                    // C# program to print DFS traversal
// from a given graph
using System;
using System.Collections.Generic;
 
// This class represents a directed graph
// using adjacency list representation
class Graph {
    private
                          int V;
 
    // Array of lists for
    // Adjacency List Representation
    private
                          List<int>[] adj;
 
    // Constructor
    Graph(int v)
                        
    {
        V = v;
        adj = new List<int>[ v ];
        for (int
                          i = 0; i < v; ++i)
            adj[i] = new List<int>();
    }
 
    // Function to Add an edge into the graph
    void
                          AddEdge(int v, int w)
    {
        // Add w to v's list.
        adj[v].Add(w);
    }
 
    // A function used by DFS
    void
                          DFSUtil(int v, bool[] visited)
    {
        // Mark the current node as visited
        // and print it
        visited[v] = true;
        Console.Write(v + " ");
 
        // Recur for all the vertices
        // adjacent to this vertex
        List<int> vList = adj[v];
        foreach(var
                          n in vList)
                        
        {
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }
 
    // The function to do DFS traversal.
    // It uses recursive DFSUtil()
    void
                          DFS(int v)
                        
    {
        // Mark all the vertices as not visited
        // (set as false by default in c#)
        bool[] visited = new bool[V];
                        
 
        // Call the recursive helper function
        // to print DFS traversal
        DFSUtil(v, visited);
    }
 
    // Driver Code
    public
                          static void Main(String[] args)
    {
        Graph g = new Graph(4);
 
        g.AddEdge(0, 1);
        g.AddEdge(0, 2);
        g.AddEdge(1, 2);
        g.AddEdge(2, 0);
        g.AddEdge(2, 3);
        g.AddEdge(3, 3);
 
        Console.WriteLine(
            "Following is Depth First Traversal "
            + "(starting from vertex 2)");
 
        // Function call
        g.DFS(2);
        Console.ReadKey();
    }
}
 
// This code is contributed by techno2mahi

                  

              
            

JavaScript

              
                
                    // Javascript program to print DFS
// traversal from a given 
                        
// graph
 
// This class represents a
                        
// directed graph using adjacency
// list representation
class Graph
{
     
    // Constructor
    constructor(v)
    {
        this.V = v;
        this.adj = new Array(v);
        for(let i = 0; i < v; i++)
            this.adj[i] = [];
    }
     
    // Function to add an edge into the graph
    addEdge(v, w)
    {
         
        // Add w to v's list.
        this.adj[v].push(w); 
    }
     
    // A function used by DFS
    DFSUtil(v, visited)
    {
         
        // Mark the current node as visited and print it
        visited[v] = true;
        console.log(v + " ");
  
        // Recur for all the vertices adjacent to this
        // vertex
        for(let i of this.adj[v].values())
        {
            let n = i
            if (!visited[n])
                this.DFSUtil(n, visited);
        }
    }
     
    // The function to do DFS traversal.
    // It uses recursive
    // DFSUtil()
    DFS(v)
                        
    {
         
        // Mark all the vertices as
        // not visited(set as
        // false by default in java)
        let visited = new Array(this.V);
                        
        for(let i = 0; i < this.V; i++)
            visited[i] = false;
  
        // Call the recursive helper
        // function to print DFS
        // traversal
        this.DFSUtil(v, visited);
    }
}
 
// Driver Code
g = new Graph(4);
  
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
 
console.log("Following is Depth First Traversal " + 
                        
               "(starting from vertex 2)");
 
g.DFS(2);
 
// This code is contributed by avanitrachhadiya2155

                  

              
            

输出

以下是深度优先遍历（从顶点2开始）
2 0 1 3

时间复杂度： O(V + E)，其中 V 是图中的顶点数，E 是图中的边数。
辅助空间： O(V + E)，因为需要额外访问大小为 V 的数组，以及迭代调用 DFS 函数的堆栈大小。

存储结构-邻接链表 可视化交互式动画版

邻接表的特点：

如何建立邻接表？

邻接表的应用：

使用邻接表的优点：

使用邻接表的缺点：

你还能读什么？

图遍历和树遍历的BFS之间的关系：

BFS 是如何工作的？

使用邻接表实现图的 BFS：

C

C++

Java

Python3

C#

Javascript

BFS相关问题：

你还可以读什么？

DFS 是如何工作的？

C++

Java

Python3

C＃

JavaScript

存储结构-邻接链表可视化交互式动画版