Kruskal(克鲁斯卡尔)算法可视化交互式动画版

在克鲁斯卡尔算法中，按升序对给定图的所有边进行排序。如果新添加的边不形成环，则继续在MST中添加新的边和节点。它首先选择最小加权边，最后选择最大加权边。因此我们可以说它在每一步中都做出局部最优选择以找到最优解。因此这是一个 贪婪算法 。

最小生成树 (MST) 或带权连通无向图的最小权重生成树是权重小于或等于所有其他生成树权重的生成树。要了解有关最小生成树的更多信息，请参阅 这篇文章 。

克鲁斯卡尔算法简介：

在这里，我们将讨论 Kruskal 算法 来查找给定加权图的 MST。

如何使用Kruskal算法求MST？

以下是使用 Kruskal 算法查找 MST 的步骤：

按权重非降序对所有边进行排序。
选择最小的边。检查是否与目前形成的生成树形成环。如果未形成循环，则包括该边。否则，丢弃它。
重复步骤#2，直到生成树中有 (V-1) 条边。

步骤2 使用并查算法来检测循环。

因此，我们建议您先阅读以下文章作为先决条件。

并查算法| 第 1 组（检测图中的循环）

并查算法| 设置 2（按等级和路径压缩联合）

Kruskal 寻找最小成本生成树的算法使用贪心方法。贪心选择是在目前构建的 MST 中选择不会引起循环的最小权重边。让我们通过一个例子来理解它：

插图：

下面是上述方法的图示：

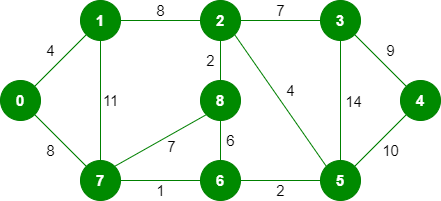
输入图：

该图包含 9 个顶点和 14 条边。因此，形成的最小生成树将具有 (9 – 1) = 8 个边。
排序后：

重量来源目的地

1 7 6

2 8 2

2 6 5

4 0 1

4 2 5

6 8 6

7 2 3

7 7 8

8 0 7

8 1 2

9 3 4

10 5 4

11 1 7

14 3 5

现在从已排序的边列表中一一挑选所有边

步骤1： 选取边7-6。没有形成循环，包括它。

在MST中添加边7-6

步骤2： 选取边8-2。 没有形成循环，包括它。

在MST中添加边8-2

步骤3： 选取边6-5。 没有形成循环，包括它。

在 MST 中添加边 6-5

步骤 4： 选取边 0-1。 没有形成循环，包括它。

在MST中添加边0-1

步骤5： 选取边2-5。 没有形成循环，包括它。

在 MST 中添加边 2-5

第6步： 选取边8-6。 由于包含该边会导致循环，因此将其丢弃。 拾取边2-3： 未形成循环，包含它。

在 MST 中添加边 2-3

步骤7： 选取边7-8。 由于包含该边会导致循环，因此将其丢弃。 选边 0-7。 没有形成循环，包括它。

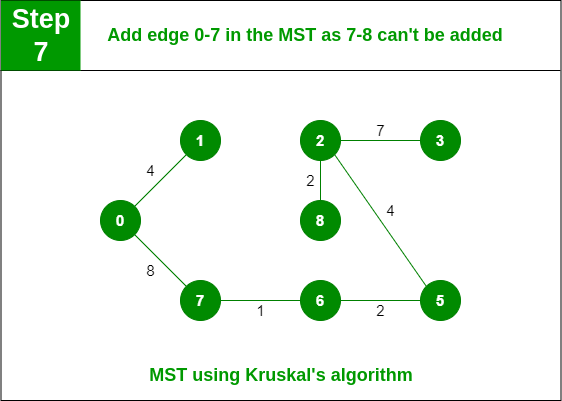
在 MST 中添加边 0-7

第8步： 选取边1-2。 由于包含该边会导致循环，因此将其丢弃。 选取边 3-4。 没有形成循环，包括它。

在MST中添加边3-4

注：由于MST包含的边数等于(V – 1)，所以算法到此停止

重量	来源	目的地
1	7	6
2	8	2
2	6	5
4	0	1
4	2	5
6	8	6
7	2	3
7	7	8
8	0	7
8	1	2
9	3	4
10	5	4
11	1	7
14	3	5

下面是上述方法的实现：

C++

              
                
                    // C++ program for the above approach 
  
#include <bits/stdc++.h> 
using namespace std; 
  
// DSU data structure 
// path compression + rank by union 
class DSU { 
    int* parent; 
    int* rank; 
  
public: 
    DSU(int n) 
    { 
        parent = new int[n]; 
        rank = new int[n]; 
  
        for (int i = 0; i < n; i++) { 
            parent[i] = -1; 
            rank[i] = 1; 
        } 
    } 
  
    // Find function 
    int
                          find(int i) 
    { 
        if (parent[i] == -1) 
            return i; 
  
        return parent[i] = find(parent[i]); 
                        
    } 
  
    // Union function 
    void unite(int x, int y) 
    { 
        int s1 = find(x); 
        int s2 = find(y); 
  
        if (s1 != s2) { 
            if (rank[s1] < rank[s2]) { 
                parent[s1] = s2; 
            } 
            else if (rank[s1] > rank[s2]) { 
                parent[s2] = s1; 
            } 
            else { 
                parent[s2] = s1; 
                rank[s1] += 1; 
            } 
        } 
    } 
}; 
  
class Graph { 
    vector<vector<int> > edgelist; 
    int
                          V; 
  
public: 
    Graph(int V) { this->V = V; } 
  
    // Function to add edge in a graph 
    void addEdge(int x, int y, int w) 
    { 
        edgelist.push_back({ w, x, y }); 
    } 
  
    void kruskals_mst() 
    { 
        // Sort all edges 
        sort(edgelist.begin(), edgelist.end()); 
  
        // Initialize the DSU 
        DSU s(V); 
        int ans = 0; 
        cout << "Following are the edges in the "
                "constructed MST"
             << endl; 
        for (auto edge : edgelist) { 
            int w = edge[0]; 
            int x = edge[1]; 
            int y = edge[2]; 
  
            // Take this edge in MST if it does 
            // not forms a cycle 
            if (s.find(x) != s.find(y)) { 
                s.unite(x, y); 
                ans += w; 
                cout << x << " -- " << y << " == " << w 
                     << endl; 
            } 
        } 
        cout << "Minimum Cost Spanning Tree: " << ans; 
    } 
}; 
  
// Driver code 
int main() 
{ 
    Graph g(4); 
    g.addEdge(0, 1, 10); 
    g.addEdge(1, 3, 15); 
    g.addEdge(2, 3, 4); 
    g.addEdge(2, 0, 6); 
    g.addEdge(0, 3, 5); 
  
                        
    // Function call 
    g.kruskals_mst(); 
  
                        
    return 0; 
}

                  

              
            

C

              
                
                    // C code to implement Kruskal's algorithm 
  
#include <stdio.h> 
#include <stdlib.h> 
  
// Comparator function to use in sorting 
int comparator(const void* p1, const void* p2) 
{ 
    const int(*x)[3] = p1; 
    const int(*y)[3] = p2; 
  
    return (*x)[2] - (*y)[2]; 
} 
  
// Initialization of parent[] and rank[] arrays 
void makeSet(int parent[], int rank[], int n) 
{ 
    for (int i = 0; i < n; i++) { 
        parent[i] = i; 
        rank[i] = 0; 
    } 
} 
  
// Function to find the parent of a node 
int findParent(int parent[], int component) 
{ 
    if
                          (parent[component] == component) 
        return component; 
  
    return parent[component] 
           = findParent(parent, parent[component]); 
} 
  
// Function to unite two sets 
void unionSet(int u, int v, int parent[], int rank[], int n) 
{ 
    // Finding the parents 
    u = findParent(parent, u); 
    v = findParent(parent, v); 
  
    if
                          (rank[u] < rank[v]) { 
        parent[u] = v; 
    } 
    else if (rank[u] > rank[v]) { 
        parent[v] = u; 
    } 
    else { 
        parent[v] = u; 
  
        // Since the rank increases if 
        // the ranks of two sets are same 
        rank[u]++; 
    } 
} 
  
// Function to find the MST 
void kruskalAlgo(int n, int edge[n][3]) 
{ 
    // First we sort the edge array in ascending order 
    // so that we can access minimum distances/cost 
    qsort(edge, n, sizeof(edge[0]), comparator); 
  
    int
                          parent[n]; 
    int
                          rank[n]; 
  
    // Function to initialize parent[] and rank[] 
    makeSet(parent, rank, n); 
  
    // To store the minimun cost 
    int
                          minCost = 0; 
  
    printf( 
        "Following are the edges in the constructed MST\n"); 
    for (int i = 0; i < n; i++) { 
        int v1 = findParent(parent, edge[i][0]); 
        int v2 = findParent(parent, edge[i][1]); 
        int wt = edge[i][2]; 
  
        // If the parents are different that 
        // means they are in different sets so 
        // union them 
        if (v1 != v2) { 
            unionSet(v1, v2, parent, rank, n); 
            minCost += wt; 
            printf("%d -- %d == %d\n", edge[i][0], 
                   edge[i][1], wt); 
        } 
    } 
  
    printf("Minimum Cost Spanning Tree: %d\n", minCost); 
} 
  
// Driver code 
int main() 
{ 
    int
                          edge[5][3] = { { 0, 1, 10 }, 
                       { 0, 2, 6 }, 
                       { 0, 3, 5 }, 
                       { 1, 3, 15 }, 
                       { 2, 3, 4 } }; 
  
                        
    kruskalAlgo(5, edge); 
  
                        
    return 0; 
}

                  

              
            

Java

              
                
                    // Java program for Kruskal's algorithm 
  
import java.util.ArrayList; 
import java.util.Comparator; 
import java.util.List; 
  
public class KruskalsMST { 
  
    // Defines edge structure 
    static
                          class Edge { 
        int src, dest, weight; 
  
        public Edge(int src, int
                          dest, int weight) 
        { 
            this.src = src; 
            this.dest = dest; 
            this.weight = weight; 
        } 
    } 
  
    // Defines subset element structure 
    static
                          class Subset { 
        int parent, rank; 
  
        public Subset(int parent, int rank) 
        { 
            this.parent = parent; 
            this.rank = rank; 
        } 
    } 
  
    // Starting point of program execution 
    public
                          static void main(String[] args) 
    { 
        int V = 4; 
        List<Edge> graphEdges = new ArrayList<Edge>( 
            List.of(new Edge(0, 1, 10), new Edge(0, 2, 6), 
                    new Edge(0, 3, 5), new Edge(1, 3, 15), 
                    new Edge(2, 3, 4))); 
  
        // Sort the edges in non-decreasing order 
        // (increasing with repetition allowed) 
        graphEdges.sort(new Comparator<Edge>() { 
            @Override public int compare(Edge o1, Edge o2) 
            { 
                return o1.weight - o2.weight; 
            } 
        }); 
  
        kruskals(V, graphEdges); 
    } 
  
    // Function to find the MST 
    private
                          static void kruskals(int V, List<Edge> edges) 
    { 
        int j = 0; 
        int noOfEdges = 0; 
  
        // Allocate memory for creating V subsets 
        Subset subsets[] = new Subset[V]; 
  
        // Allocate memory for results 
        Edge results[] = new Edge[V]; 
  
        // Create V subsets with single elements 
        for (int
                          i = 0; i < V; i++) { 
            subsets[i] = new Subset(i, 0); 
                        
        } 
  
        // Number of edges to be taken is equal to V-1 
        while (noOfEdges < V - 1) { 
  
            // Pick the smallest edge. And increment 
            // the index for next iteration 
            Edge nextEdge = edges.get(j); 
            int x = findRoot(subsets, nextEdge.src); 
                        
            int y = findRoot(subsets, nextEdge.dest); 
                        
  
            // If including this edge doesn't cause cycle, 
            // include it in result and increment the index 
            // of result for next edge 
            if (x != y) { 
                results[noOfEdges] = nextEdge; 
                union(subsets, x, y); 
                noOfEdges++; 
            } 
  
            j++; 
        } 
  
        // Print the contents of result[] to display the 
        // built MST 
        System.out.println( 
            "Following are the edges of the constructed MST:"); 
        int minCost = 0; 
        for (int
                          i = 0; i < noOfEdges; i++) { 
            System.out.println(results[i].src + " -- "
                        
                               + results[i].dest + " == "
                               + results[i].weight); 
            minCost += results[i].weight; 
        } 
        System.out.println("Total cost of MST: "
                          + minCost); 
    } 
  
                        
    // Function to unite two disjoint sets 
    private
                          static void union(Subset[] subsets, int x, 
                              int y) 
    { 
        int rootX = findRoot(subsets, x); 
        int rootY = findRoot(subsets, y); 
  
                        
        if (subsets[rootY].rank < subsets[rootX].rank) { 
            subsets[rootY].parent = rootX; 
        } 
        else if (subsets[rootX].rank 
                 < subsets[rootY].rank) { 
            subsets[rootX].parent = rootY; 
        } 
        else { 
            subsets[rootY].parent = rootX; 
            subsets[rootX].rank++; 
        } 
    } 
  
                        
    // Function to find parent of a set 
    private
                          static int findRoot(Subset[] subsets, int i) 
    { 
        if (subsets[i].parent == i) 
            return subsets[i].parent; 
  
                        
        subsets[i].parent 
            = findRoot(subsets, subsets[i].parent); 
        return subsets[i].parent; 
    } 
} 
// This code is contributed by Salvino D'sa

                  

              
            

Python3

              
                
                    # Python program for Kruskal's algorithm to find 
# Minimum Spanning Tree of a given connected, 
# undirected and weighted graph 
  
  
# Class to represent a graph 
class Graph: 
  
    def
                          __init__(self, vertices): 
        self.V = vertices 
        self.graph =
                          [] 
  
    # Function to add an edge to graph 
    def
                          addEdge(self, u, v, w): 
        self.graph.append([u, v, w]) 
  
    # A utility function to find set of an element i 
    # (truly uses path compression technique) 
    def
                          find(self, parent, i): 
        if parent[i] != i: 
  
            # Reassignment of node's parent 
            # to root node as 
            # path compression requires 
            parent[i] = self.find(parent, parent[i]) 
        return parent[i] 
  
    # A function that does union of two sets of x and y 
    # (uses union by rank) 
    def
                          union(self, parent, rank, x, y): 
  
        # Attach smaller rank tree under root of 
        # high rank tree (Union by Rank) 
        if rank[x] < rank[y]: 
            parent[x] = y 
                        
        elif rank[x] > rank[y]: 
            parent[y] = x 
                        
  
        # If ranks are same, then make one as root 
        # and increment its rank by one 
        else: 
            parent[y] = x 
                        
            rank[x] +=
                          1
  
    # The main function to construct MST 
    # using Kruskal's algorithm 
    def
                          KruskalMST(self): 
  
        # This will store the resultant MST 
        result = [] 
                        
  
        # An index variable, used for sorted edges 
        i = 0
  
        # An index variable, used for result[] 
        e = 0
  
        # Sort all the edges in 
        # non-decreasing order of their 
        # weight 
        self.graph =
                          sorted(self.graph, 
                            key=lambda
                          item: item[2]) 
  
        parent = [] 
                        
        rank = [] 
                        
  
        # Create V subsets with single elements 
        for node in
                          range(self.V): 
            parent.append(node) 
            rank.append(0) 
                        
  
        # Number of edges to be taken is less than to V-1 
        while e < self.V - 1: 
  
            # Pick the smallest edge and increment 
            # the index for next iteration 
            u, v, w = self.graph[i] 
            i = i + 1
            x = self.find(parent, u) 
            y = self.find(parent, v) 
  
            # If including this edge doesn't 
            # cause cycle, then include it in result 
            # and increment the index of result 
            # for next edge 
            if x != y: 
                e = e + 1
                result.append([u, v, w]) 
                self.union(parent, rank, x, y) 
            # Else discard the edge 
  
        minimumCost = 0
                        
        print("Edges in the constructed MST") 
        for u, v, weight in result: 
            minimumCost += weight 
            print("%d -- %d == %d" % (u, v, weight)) 
        print("Minimum Spanning Tree", minimumCost) 
                        
  
  
# Driver code 
if __name__ ==
                          '__main__': 
    g = Graph(4) 
    g.addEdge(0, 1, 10) 
    g.addEdge(0, 2, 6) 
    g.addEdge(0, 3, 5) 
    g.addEdge(1, 3, 15) 
    g.addEdge(2, 3, 4) 
  
                        
    # Function call 
    g.KruskalMST() 
  
                        
# This code is contributed by Neelam Yadav 
# Improved by James Graça-Jones 

                  

              
            

C#

              
                
                    // C# Code for the above approach 
  
using System; 
  
class Graph { 
  
    // A class to represent a graph edge 
    class
                          Edge : IComparable<Edge> { 
        public int src, dest, weight; 
  
        // Comparator function used for sorting edges 
        // based on their weight 
        public int CompareTo(Edge compareEdge) 
        { 
            return this.weight - compareEdge.weight; 
        } 
    } 
  
    // A class to represent 
    // a subset for union-find 
    public
                          class subset { 
        public int parent, rank; 
    }; 
  
    // V-> no. of vertices & E->no.of edges 
    int
                          V, E; 
  
    // Collection of all edges 
    Edge[] edge; 
  
    // Creates a graph with V vertices and E edges 
    Graph(int v, int e) 
                        
    { 
        V = v; 
        E = e; 
        edge = new Edge[E]; 
        for (int
                          i = 0; i < e; ++i) 
            edge[i] = new Edge(); 
    } 
  
    // A utility function to find set of an element i 
    // (uses path compression technique) 
    int
                          find(subset[] subsets, int i) 
    { 
        // Find root and make root as 
        // parent of i (path compression) 
        if (subsets[i].parent != i) 
            subsets[i].parent 
                = find(subsets, subsets[i].parent); 
  
        return subsets[i].parent; 
    } 
  
    // A function that does union of 
    // two sets of x and y (uses union by rank) 
    void
                          Union(subset[] subsets, int x, int y) 
                        
    { 
        int xroot = find(subsets, x); 
        int yroot = find(subsets, y); 
  
        // Attach smaller rank tree under root of 
        // high rank tree (Union by Rank) 
        if (subsets[xroot].rank < subsets[yroot].rank) 
            subsets[xroot].parent = yroot; 
        else if (subsets[xroot].rank > subsets[yroot].rank) 
            subsets[yroot].parent = xroot; 
  
        // If ranks are same, then make one as root 
        // and increment its rank by one 
        else { 
            subsets[yroot].parent = xroot; 
            subsets[xroot].rank++; 
        } 
    } 
  
    // The main function to construct MST 
    // using Kruskal's algorithm 
    void
                          KruskalMST() 
    { 
        // This will store the 
        // resultant MST 
        Edge[] result = new Edge[V]; 
  
        // An index variable, used for result[] 
        int e = 0; 
  
        // An index variable, used for sorted edges 
        int i = 0; 
        for (i = 0; i < V; ++i) 
            result[i] = new Edge(); 
  
        // Sort all the edges in non-decreasing 
        // order of their weight. If we are not allowed 
        // to change the given graph, we can create 
        // a copy of array of edges 
        Array.Sort(edge); 
  
        // Allocate memory for creating V subsets 
        subset[] subsets = new subset[V]; 
        for (i = 0; i < V; ++i) 
            subsets[i] = new subset(); 
  
                        
        // Create V subsets with single elements 
        for (int
                          v = 0; v < V; ++v) { 
            subsets[v].parent = v; 
            subsets[v].rank = 0; 
        } 
        i = 0; 
  
                        
        // Number of edges to be taken is equal to V-1 
        while (e < V - 1) { 
  
                        
            // Pick the smallest edge. And increment 
            // the index for next iteration 
            Edge next_edge = new Edge(); 
            next_edge = edge[i++]; 
  
                        
            int x = find(subsets, next_edge.src); 
                        
            int y = find(subsets, next_edge.dest); 
                        
  
                        
            // If including this edge doesn't cause cycle, 
            // include it in result and increment the index 
            // of result for next edge 
            if (x != y) { 
                result[e++] = next_edge; 
                Union(subsets, x, y); 
            } 
        } 
  
                        
        // Print the contents of result[] to display 
        // the built MST 
        Console.WriteLine("Following are the edges in "
                          + "the constructed MST"); 
  
                        
        int minimumCost = 0; 
        for (i = 0; i < e; ++i) { 
            Console.WriteLine(result[i].src + " -- "
                        
                              + result[i].dest 
                              + " == " + result[i].weight); 
            minimumCost += result[i].weight; 
        } 
  
                        
        Console.WriteLine("Minimum Cost Spanning Tree: "
                          + minimumCost); 
        Console.ReadLine(); 
    } 
  
                        
    // Driver's Code 
    public
                          static void Main(String[] args) 
    { 
        int V = 4; 
        int E = 5; 
        Graph graph = new Graph(V, E); 
  
                        
        // add edge 0-1 
        graph.edge[0].src = 0; 
        graph.edge[0].dest = 1; 
        graph.edge[0].weight = 10; 
  
                        
        // add edge 0-2 
        graph.edge[1].src = 0; 
        graph.edge[1].dest = 2; 
        graph.edge[1].weight = 6; 
  
                        
        // add edge 0-3 
        graph.edge[2].src = 0; 
        graph.edge[2].dest = 3; 
        graph.edge[2].weight = 5; 
  
                        
        // add edge 1-3 
        graph.edge[3].src = 1; 
        graph.edge[3].dest = 3; 
        graph.edge[3].weight = 15; 
  
                        
        // add edge 2-3 
        graph.edge[4].src = 2; 
        graph.edge[4].dest = 3; 
        graph.edge[4].weight = 4; 
  
                        
        // Function call 
        graph.KruskalMST(); 
    } 
} 
  
                        
// This code is contributed by Aakash Hasija

                  

              
            

Javascript

              
                
                    <script>  
// JavaScript implementation of the krushkal's algorithm.  
                        
  
function makeSet(parent,rank,n) 
{ 
    for(let i=0;i<n;i++) 
    { 
        parent[i]=i; 
        rank[i]=0; 
    } 
} 
  
function findParent(parent,component) 
{ 
    if(parent[component]==component) 
        return component; 
  
    return
                          parent[component] = findParent(parent,parent[component]); 
} 
  
function unionSet(u, v, parent, rank,n) 
{ 
    //this function unions two set on the basis of rank 
    //as shown below 
    u=findParent(parent,u); 
    v=findParent(parent,v); 
  
    if(rank[u]<rank[v]) 
    { 
        parent[u]=v; 
    } 
    else
                          if(rank[u]<rank[v]) 
    { 
        parent[v]=u; 
    } 
    else
                        
    { 
        parent[v]=u; 
        rank[u]++;//since the rank increases if the ranks of two sets are same 
    } 
} 
  
function kruskalAlgo(n, edge) 
{ 
    //First we sort the edge array in ascending order 
    //so that we can access minimum distances/cost 
    edge.sort((a, b)=>{ 
        return a[2] - b[2]; 
    }) 
    //inbuilt quick sort function comes with stdlib.h 
    //go to https://www.geeksforgeeks.org/comparator-function-of-qsort-in-c/ 
                        
    //if there is any doubt regarding the function 
    let parent = new Array(n); 
    let rank = new Array(n); 
  
    makeSet(parent,rank,n);//function to initialize parent[] and rank[] 
  
    let minCost=0;//to store the minimun cost 
  
    document.write("Following are the edges in the constructed MST"); 
    for(let i=0;i<n;i++) 
    { 
        let v1=findParent(parent,edge[i][0]); 
        let v2=findParent(parent,edge[i][1]); 
        let wt=edge[i][2]; 
  
        if(v1!=v2)//if the parents are different that means they are in 
                  //different sets so union them 
        { 
            unionSet(v1,v2,parent,rank,n); 
            minCost+=wt; 
            document.write(edge[i][0] + " -- " + edge[i][1] + " == " + wt); 
        } 
    } 
  
    document.write("Minimum Cost Spanning Tree:",minCost); 
                        
} 
  
  
//Here 5 is the number of edges, can be asked from the user 
//when making the graph through user input 
//3 represents the no of index positions for storing u --> v(adjacent vertices)  
                        
//and its cost/distance; 
                        
let edge = [ 
        [0,1,10], 
        [0,2,6], 
        [0,3,5], 
        [1,3,15], 
        [2,3,4] 
]; 
  
kruskalAlgo(5,edge); 
  
// The code is contributed by Arushi Jindal.  
</script>

                  

              
            

输出

以下是构建的 MST 中的边
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
最小成本生成树：19

时间复杂度： O(E * logE) 或 O(E * logV)

边排序需要 O(E * logE) 时间。
排序后，我们迭代所有边并应用查找并集算法。查找和并集操作最多需要 O(logV) 时间。
所以总体复杂度是 O(E * logE + E * logV) 时间。
E的值最多可以是O(V ² )，因此O(logV)和O(logE)是相同的。因此，总体时间复杂度为 O(E * logE) 或 O(E*logV)

辅助空间： O(V + E)，其中V是图中的顶点数，E是图中的边数。

本文由 Aashish Barnwal编译，并由图码团队审核。如果您发现任何不正确的内容，或者您想分享有关上述主题的更多信息，请发表评论。