栈-表达式计算-顺序表可视化交互式动画版

编写一个程序将 Infix 表达式转换为 Postfix 形式。

中缀表达式： “a 运算符 b”(a + b) 形式的表达式，即当运算符位于每对操作数之间时。
后缀表达式： “ab 运算符”(ab+) 形式的表达式，即每对操作数后面都跟有一个运算符。

例子：

输入： A + B * C + D
输出： ABC*+D+

输入： ((A + B) – C * (D / E)) + F
输出： AB+CDE/*-F+

为什么用后缀表示表达式？

编译器从左到右或从右到左扫描表达式。
考虑表达式： a + b * c + d

编译器首先扫描表达式以计算表达式 b * c，然后再次扫描表达式以向其添加 a。
然后在另一次扫描后将结果添加到 d 中。

重复扫描使得效率非常低。中缀表达式很容易被人类读取和求解，而计算机无法轻松地区分运算符和括号，因此，最好在计算之前将表达式转换为后缀（或前缀）形式。

后缀形式对应的表达式是 abc*+d+ 。可以使用堆栈轻松计算后缀表达式。

如何将中缀表达式转换为后缀表达式？

要将中缀表达式转换为后缀表达式，请使用 堆栈数据结构 。从左到右扫描中缀表达式。每当我们得到一个操作数时，将其添加到后缀表达式中，如果我们得到一个运算符或括号，则通过保持其优先级将其添加到堆栈中。

下面是实现上述想法的步骤：

从左到右 扫描中缀表达式。
如果扫描到的字符是操作数，则将其放入后缀表达式中。
否则，请执行以下操作
- 如果扫描到的运算符的优先级和结合性大于栈中运算符的优先级和结合性[或者栈为空或栈中包含'(']，则将其压入栈中。[' ^ ' 运算符是右关联的，而其他运算符如“ + ”、“ - ”、“ * ”和“ / ”是左关联]。
  - 特别检查堆栈顶部的运算符和扫描的运算符均为“ ^ ”时的情况。在这种情况下，由于其右结合性，扫描运算符的优先级较高。所以它会被压入操作符栈。
  - 在所有其他情况下，当运算符堆栈的顶部与扫描的运算符相同时，则从堆栈中弹出该运算符，因为左关联性导致扫描的运算符具有较低的优先级。
- 否则，从堆栈中弹出所有优先级大于或等于扫描到的运算符的运算符。
  - 完成此操作后，将扫描的运算符推入堆栈。（如果在弹出时遇到括号，则停在那里并将扫描的运算符推入堆栈。）
如果扫描到的字符是' ( '，则将其压入堆栈。
如果扫描到的字符是' ) '，则出栈并输出，直到遇到' ( '，并丢弃两个括号。
重复步骤 2-5 ，直到扫描到中缀表达式。
扫描结束后，弹出堆栈并添加后缀表达式中的运算符，直到不为空。
最后，打印后缀表达式。

插图：

请按照下图更好地理解

考虑中缀表达式 exp = “a+b*c+d”并使用迭代器 i
扫描中缀表达式，迭代器初始化为 i = 0 。

第一步： 这里 i = 0 且 exp[i] = 'a' 即操作数。所以将其添加到后缀表达式中。因此， postfix =“a” 。

在后缀中添加“a”

第二步： 这里 i = 1 且 exp[i] = '+' 即运算符。将其推入堆栈。 postfix = “a” 和 stack = {+} 。

将“+”压入堆栈

第三步： 现在 i = 2 且 exp[i] = 'b' 即操作数。所以将其添加到后缀表达式中。 后缀 = “ab” 和 堆栈 = {+} 。

在后缀中添加“b”

第四步： 现在 i = 3 且 exp[i] = '*' 即一个运算符。将其推入堆栈。 postfix = “ab” 和 stack = {+, *} 。

将“*”压入堆栈

第五步： 现在 i = 4 且 exp[i] = 'c' 即操作数。将其添加到后缀表达式中。 postfix = “abc” 和 stack = {+, *} 。

在后缀中添加“c”

第六步： 现在 i = 5 且 exp[i] = '+' 即一个运算符。堆栈最顶层的元素具有更高的优先级。因此弹出直到堆栈变空或顶部元素的优先级较低。 '*' 被弹出并添加到后缀中。所以 postfix = “abc*” 和 stack = {+} 。

弹出“*”并添加后缀

现在顶部元素是“ + ”，它的优先级也没有降低。弹出它。 后缀=“abc*+” 。

弹出“+”并将其添加到后缀中

现在堆栈是空的。因此将 “+” 压入堆栈。 堆栈= {+} 。

将“+”压入堆栈

第七步： 现在 i = 6 且 exp[i] = 'd' 即操作数。将其添加到后缀表达式中。 后缀=“abc*+d” 。

在后缀中添加“d”

最后一步： 现在没有留下任何元素。因此清空堆栈并将其添加到后缀表达式中。 后缀=“abc*+d+” 。

弹出“+”并将其添加到后缀中

下面是上述算法的实现：

C++14

            
              
                  // C++ code to convert infix expression to postfix
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to return precedence of operators
int prec(char c)
                      
{
    if
                        (c == '^')
                      
        return 3;
    else
                        if (c == '/' || c == '*')
                      
        return 2;
    else
                        if (c == '+' || c == '-')
                      
        return 1;
    else
                      
        return -1;
}
 
// The main function to convert infix expression
// to postfix expression
                      
void infixToPostfix(string s)
{
 
    stack<char> st;
    string result;
 
    for
                        (int i = 0; i < s.length(); i++) {
                      
        char c = s[i];
 
        // If the scanned character is
        // an operand, add it to output string.
        if ((c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z')
            || (c >= '0' && c <= '9'))
            result += c;
 
        // If the scanned character is an
        // ‘(‘, push it to the stack.
        else if (c == '(')
            st.push('(');
                      
 
        // If the scanned character is an ‘)’,
        // pop and add to output string from the stack
        // until an ‘(‘ is encountered.
        else if (c == ')') {
                      
            while (st.top() != '(') {
                result += st.top();
                st.pop();
            }
            st.pop();
        }
 
        // If an operator is scanned
        else {
            while (!st.empty()
                   && prec(s[i]) <= prec(st.top())) {
                result += st.top();
                st.pop();
            }
            st.push(c);
        }
    }
 
    // Pop all the remaining elements from the stack
    while (!st.empty()) {
        result += st.top();
        st.pop();
    }
 
    cout << result << endl;
}
 
// Driver code
int main()
{
    string exp = "a+b*(c^d-e)^(f+g*h)-i";
 
    // Function call
    infixToPostfix(exp);
   
                      
    return 0;
}

                

            
          

C

            
              
                  // C code to convert infix to postfix expression
 
#include <stdio.h>
                      
#include <stdlib.h>
                      
#include <string.h>
                      
 
#define MAX_EXPR_SIZE 100
                      
 
// Function to return precedence of operators
int precedence(char operator)
{
    switch (operator) {
    case
                        '+':
                      
    case
                        '-':
                      
        return 1;
    case
                        '*':
                      
    case
                        '/':
                      
        return 2;
    case
                        '^':
                      
        return 3;
    default:
        return -1;
    }
}
 
// Function to check if the scanned character 
// is an operator
int isOperator(char ch)
{
    return (ch == '+' || ch == '-'
                        || ch == '*' || ch == '/'
            || ch == '^');
                      
}
 
// Main functio to convert infix expression
// to postfix expression
                      
char* infixToPostfix(char* infix)
{
    int
                        i, j;
                      
    int
                        len = strlen(infix);
                      
    char* postfix = (char*)malloc(sizeof(char) * (len + 2));
    char
                        stack[MAX_EXPR_SIZE];
    int
                        top = -1;
                      
 
    for
                        (i = 0, j = 0; i < len; i++) {
                      
        if (infix[i] == ' ' || infix[i] == '\t')
            continue;
       
        // If the scanned character is operand
        // add it to the postfix expression
        if (isalnum(infix[i])) {
            postfix[j++] = infix[i];
        }
       
        // if the scanned character is '('
        // push it in the stack
        else if (infix[i] == '(') {
            stack[++top] = infix[i];
        }
       
        // if the scanned character is ')'
        // pop the stack and add it to the 
        // output string until empty or '(' found
        else if (infix[i] == ')') {
            while (top > -1 && stack[top] != '(')
                postfix[j++] = stack[top--];
            
                      
                top--;
        }
       
        // If the scanned character is an operator
        // push it in the stack
        else if (isOperator(infix[i])) {
            while (top > -1
                   && precedence(stack[top])
                          >= precedence(infix[i]))
                postfix[j++] = stack[top--];
            stack[++top] = infix[i];
        }
    }
 
    // Pop all remaining elements from the stack
    while (top > -1) {
        if (stack[top] == '(') {
            return "Invalid Expression";
        }
        postfix[j++] = stack[top--];
    }
    postfix[j] = '\0';
                      
    return postfix;
}
 
// Driver code
int main()
{
    char
                        infix[MAX_EXPR_SIZE] = "a+b*(c^d-e)^(f+g*h)-i";
   
                      
    // Function call
    char* postfix = infixToPostfix(infix);
                      
    printf("%s\n", postfix);
    free(postfix);
    return 0;
}

                

            
          

Java

            
              
                  // Java code to convert infix expression to postfix
 
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Stack;
 
class Test {
 
    // A utility function to return
    // precedence of a given operator
    // Higher returned value means
    // higher precedence
    static
                        int Prec(char ch)
                      
    {
        switch (ch) {
        case '+':
                      
        case '-':
                      
            return 1;
 
        case '*':
                      
        case '/':
                      
            return 2;
 
        case '^':
                      
            return 3;
        }
        return -1;
    }
 
    // The main method that converts
    // given infix expression
    // to postfix expression.
    static
                        String infixToPostfix(String exp)
                      
    {
        // Initializing empty String for result
        String result = new String("");
                      
 
        // Initializing empty stack
        Deque<Character> stack
            = new ArrayDeque<Character>();
 
        for (int
                        i = 0; i < exp.length(); ++i) {
                      
            char c = exp.charAt(i);
 
            // If the scanned character is an
            // operand, add it to output.
            if (Character.isLetterOrDigit(c))
                result += c;
 
            // If the scanned character is an '(',
            // push it to the stack.
            else if (c == '(')
                stack.push(c);
 
            // If the scanned character is an ')',
            // pop and output from the stack
            // until an '(' is encountered.
            else if (c == ')') {
                      
                while (!stack.isEmpty()
                       && stack.peek() != '(') {
                    result += stack.peek();
                    stack.pop();
                }
 
                stack.pop();
            }
           
                      
            // An operator is encountered
            else
            {
                while (!stack.isEmpty()
                       && Prec(c) <= Prec(stack.peek())) {
 
                    result += stack.peek();
                    stack.pop();
                }
                stack.push(c);
            }
        }
 
        // Pop all the operators from the stack
        while (!stack.isEmpty()) {
            if (stack.peek() == '(')
                return "Invalid Expression";
            result += stack.peek();
            stack.pop();
        }
       
        return result;
    }
 
    // Driver code 
    public
                        static void main(String[] args)
                      
    {
        String exp = "a+b*(c^d-e)^(f+g*h)-i";
       
          // Function call
        System.out.println(infixToPostfix(exp));
    }
}

                

            
          

Python3

            
              
                  # Python program to convert infix expression to postfix
 
 
# Class to convert the expression
class Conversion:
 
    # Constructor to initialize the class variables
    def
                        __init__(self, capacity):
                      
        self.top =
                        -1
                      
        self.capacity =
                        capacity
         
        # This array is used a stack
        self.array =
                        []
                      
         
        # Precedence setting
        self.output =
                        []
                      
        self.precedence = {'+': 1, '-': 1, '*': 2, '/': 2, '^': 3}
 
    # Check if the stack is empty
    def
                        isEmpty(self):
                      
        return True if
                        self.top == -1 else False
                      
 
    # Return the value of the top of the stack
    def
                        peek(self):
                      
        return self.array[-1]
 
    # Pop the element from the stack
    def
                        pop(self):
                      
        if not self.isEmpty():
            self.top -= 1
            return self.array.pop()
        else:
            return "$"
 
    # Push the element to the stack
    def
                        push(self, op):
                      
        self.top += 1
        self.array.append(op)
 
    # A utility function to check is the given character
    # is operand
    def
                        isOperand(self, ch):
                      
        return ch.isalpha()
 
    # Check if the precedence of operator is strictly
    # less than top of stack or not
    def
                        notGreater(self, i):
                      
        try:
            a = self.precedence[i]
            b = self.precedence[self.peek()]
            return True if
                        a <=
                        b else False
                      
        except KeyError:
            return False
 
    # The main function that
    # converts given infix expression
    # to postfix expression
    def
                        infixToPostfix(self, exp):
                      
 
        # Iterate over the expression for conversion
        for i in
                        exp:
                      
             
                      
            # If the character is an operand,
            # add it to output
            if self.isOperand(i):
                self.output.append(i)
 
            # If the character is an '(', push it to stack
            elif i == '(':
                self.push(i)
 
            # If the scanned character is an ')', pop and
            # output from the stack until and '(' is found
            elif i == ')':
                while((not
                        self.isEmpty()) and
                      
                      self.peek() !=
                        '('):
                      
                    a = self.pop()
                    self.output.append(a)
                if (not self.isEmpty() and self.peek() != '('):
                    return -1
                      
                else:
                    self.pop()
 
            # An operator is encountered
            else:
                while(not
                        self.isEmpty() and self.notGreater(i)):
                      
                    self.output.append(self.pop())
                self.push(i)
 
        # Pop all the operator from the stack
        while not self.isEmpty():
            self.output.append(self.pop())
 
        for ch in
                        self.output:
                      
            print(ch, end="")
 
 
# Driver code
if __name__ ==
                        '__main__':
                      
    exp = "a+b*(c^d-e)^(f+g*h)-i"
    obj = Conversion(len(exp))
 
    # Function call
    obj.infixToPostfix(exp)
 
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

                

            
          

C#

            
              
                  // C# code to convert infix expression to postfix*/
 
using System;
using System.Collections.Generic;
 
public class Test {
 
    // A utility function to return
    // precedence of a given operator
    // Higher returned value means higher precedence
    internal
                        static int Prec(char
                        ch)
                      
    {
        switch (ch) {
        case '+':
                      
        case '-':
                      
            return 1;
 
        case '*':
                      
        case '/':
                      
            return 2;
 
        case '^':
                      
            return 3;
        }
        return -1;
    }
 
    // The main method that converts given infix expression
    // to postfix expression.
    public
                        static string infixToPostfix(string exp)
                      
    {
        // Initializing empty String for result
        string result = "";
 
        // Initializing empty stack
        Stack<char> stack = new Stack<char>();
 
        for (int
                        i = 0; i < exp.Length; ++i) {
                      
            char c = exp[i];
 
            // If the scanned character is an
            // operand, add it to output.
            if (char.IsLetterOrDigit(c)) {
                result += c;
            }
 
            // If the scanned character is an '(',
            // push it to the stack.
            else if (c == '(') {
                      
                stack.Push(c);
            }
 
            // If the scanned character is an ')',
            // pop and output from the stack
            // until an '(' is encountered.
            else if (c == ')') {
                      
                while (stack.Count > 0
                       && stack.Peek() != '(') {
                    result += stack.Pop();
                }
 
                if (stack.Count > 0
                    && stack.Peek() != '(') {
                    return "Invalid Expression";
                }
                else {
                    stack.Pop();
                }
            }
           
                      
            // An operator is encountered
            else
            {
                while (stack.Count > 0
                       && Prec(c) <= Prec(stack.Peek())) {
                    result += stack.Pop();
                }
                stack.Push(c);
            }
        }
 
        // Pop all the operators from the stack
        while (stack.Count > 0) {
            result += stack.Pop();
        }
 
        return result;
    }
 
    // Driver code
    public
                        static void Main(string[] args)
                      
    {
        string exp = "a+b*(c^d-e)^(f+g*h)-i";
       
        // Function call
        Console.WriteLine(infixToPostfix(exp));
    }
}
 
// This code is contributed by Shrikant13

                

            
          

Javascript

            
              
                      /* Javascript implementation to convert
    infix expression to postfix*/
     
    //Function to return precedence of operators
    function
                        prec(c) {
        if(c == '^')
            return 3;
        else if(c == '/' || c=='*')
            return 2;
        else if(c == '+' || c == '-')
                      
            return 1;
        else
            return -1;
    }
 
    // The main function to convert infix expression
    //to postfix expression
    function
                        infixToPostfix(s) {
 
        let st = []; //For stack operations, we are using JavaScript built in stack
        let result = "";
                      
 
        for(let i = 0; i < s.length; i++) {
                      
            let c = s[i];
 
            // If the scanned character is
            // an operand, add it to output string.
            if((c >= 'a'
                        && c <= 'z') || (c >= 'A' && c <= 'Z') || (c >= '0' && c <= '9'))
                result += c;
 
            // If the scanned character is an
            // ‘(‘, push it to the stack.
            else if(c == '(')
                st.push('(');
                      
 
            // If the scanned character is an ‘)’,
            // pop and to output string from the stack
            // until an ‘(‘ is encountered.
            else if(c == ')') {
                      
                while(st[st.length - 1] != '(')
                {
                    result += st[st.length - 1];
                    st.pop();
                }
                st.pop();
            }
 
            //If an operator is scanned
            else {
                while(st.length != 0 && prec(s[i]) <= prec(st[st.length - 1])) {
                      
                    result += st[st.length - 1];
                    st.pop(); 
                }
                st.push(c);
            }
        }
 
        // Pop all the remaining elements from the stack
        while(st.length != 0) {
            result += st[st.length - 1];
            st.pop();
        }
 
        document.write(result + "</br>");
    }
     
    let exp = "a+b*(c^d-e)^(f+g*h)-i";
    infixToPostfix(exp);
 
// This code is contributed by decode2207.

                

            
          

输出

abcd^e-fgh*+^*+i-

时间复杂度： O(N)，其中 N 是中缀表达式的大小
辅助空间： O(N)，其中 N 是中缀表达式的大小

如果您发现任何不正确的内容，或者您想分享有关上述主题的更多信息，请发表评论。

给定一个中缀表达式，任务是将其转换为前缀表达式。

中缀表达式： a '运算符' b 类型的表达式（a+b，其中 + 是运算符），即当运算符位于两个操作数之间时。

前缀表达式： “ 运算符”ab 类型的表达式（+ab，其中 + 是运算符），即当运算符置于操作数之前时。

例子：

输入： A*B+C/D
输出： +*AB/CD

输入： (A – B/C) * (A/KL)
输出： *-A/BC-/AKL

如何将中缀表达式转换为前缀表达式？

要将中缀表达式转换为前缀表达式，我们可以使用 堆栈数据结构 。想法如下：

步骤 1： 反转中缀表达式。请注意，反转时每个“(”将变为“)”，每个“)”将变为“(”。

步骤2： 将反转的中 缀表达式转换为“nearly”后缀表达式 。

在转换为后缀表达式时，我们不会使用弹出操作来弹出优先级大于或等于的运算符，这里我们只将优先级更高的运算符从堆栈中弹出。

步骤3： 反转后缀表达式。

堆栈用于将中缀表达式转换为后缀形式。

插图：

请参阅下图以获得清晰的想法：

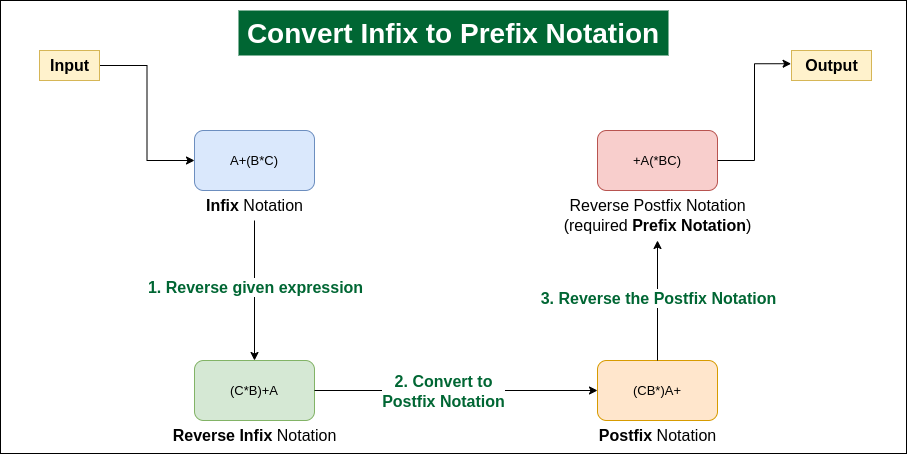
将中缀表达式转换为前缀表达式

下面是该算法的 C++ 实现。

C++
Java
Python3
C＃
JavaScript

C++

            
              
                  // C++ program to convert infix to prefix
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if the character is an operator
bool isOperator(char c)
{
    return (!isalpha(c) && !isdigit(c));
}
 
// Function to get the priority of operators
int getPriority(char C)
{
    if
                        (C == '-' || C == '+')
        return 1;
    else
                        if (C == '*' || C == '/')
        return 2;
    else
                        if (C == '^')
        return 3;
    return 0;
}
 
// Function to convert the infix expression to postfix
string infixToPostfix(string infix)
{
    infix = '(' + infix + ')';
                      
    int
                        l = infix.size();
    stack<char> char_stack;
    string output;
 
    for
                        (int i = 0; i < l; i++) {
 
        // If the scanned character is an
        // operand, add it to output.
        if (isalpha(infix[i]) || isdigit(infix[i]))
            output += infix[i];
 
        // If the scanned character is an
        // ‘(‘, push it to the stack.
        else if (infix[i] == '(')
                      
            char_stack.push('(');
 
        // If the scanned character is an
        // ‘)’, pop and output from the stack
        // until an ‘(‘ is encountered.
        else if (infix[i] == ')') {
            while (char_stack.top() != '(') {
                output += char_stack.top();
                char_stack.pop();
            }
 
            // Remove '(' from the stack
            char_stack.pop();
        }
 
        // Operator found
        else {
            if (isOperator(char_stack.top())) {
                      
                if (infix[i] == '^') {
                    while (
                        getPriority(infix[i])
                        <= getPriority(char_stack.top())) {
                        output += char_stack.top();
                        char_stack.pop();
                    }
                }
                else {
                    while (
                        getPriority(infix[i])
                        < getPriority(char_stack.top())) {
                        output += char_stack.top();
                        char_stack.pop();
                    }
                }
 
                // Push current Operator on stack
                char_stack.push(infix[i]);
            }
        }
    }
    while (!char_stack.empty()) {
        output += char_stack.top();
        char_stack.pop();
    }
    return output;
}
 
// Function to convert infix to prefix notation
string infixToPrefix(string infix)
{
    // Reverse String and replace ( with ) and vice versa
    // Get Postfix
    // Reverse Postfix
    int
                        l = infix.size();
 
    // Reverse infix
    reverse(infix.begin(), infix.end());
 
    // Replace ( with ) and vice versa
    for
                        (int i = 0; i < l; i++) {
 
        if (infix[i] == '(') {
            infix[i] = ')';
                      
        }
        else if (infix[i] == ')') {
            infix[i] = '(';
                      
        }
    }
 
    string prefix = infixToPostfix(infix);
 
    // Reverse postfix
    reverse(prefix.begin(), prefix.end());
 
    return prefix;
}
 
// Driver code
int main()
{
    string s = ("x+y*z/w+u");
   
                      
    // Function call
    cout << infixToPrefix(s) << std::endl;
    return 0;
}

                

            
          

Java

            
              
                  // Java program to convert infix to prefix
import java.util.*;
 
class GFG {
    // Function to check if the character is an operand
    static
                        boolean isalpha(char c)
    {
        if (c >= 'a'
                        && c <= 'z' || c >= 'A' && c <= 'Z') {
            return true;
                      
        }
        return false;
                      
    }
 
    // Function to check if the character is digit
    static
                        boolean isdigit(char c)
    {
        if (c >= '0'
                        && c <= '9') {
            return true;
                      
        }
        return false;
                      
    }
 
    // Function to check if the character is an operator
    static
                        boolean isOperator(char c)
    {
        return (!isalpha(c) && !isdigit(c));
                      
    }
 
    // Function to get priority of operators
    static
                        int getPriority(char C)
    {
        if (C == '-'
                        || C == '+')
                      
            return 1;
        else if (C == '*' || C == '/')
            return 2;
        else if (C == '^')
            return 3;
 
        return 0;
    }
 
    // Reverse the letters of the word
    static
                        String reverse(char str[], int start, int end)
                      
    {
        // Temporary variable to store character
        char temp;
        while (start < end) {
            // Swapping the first and last character
            temp = str[start];
            str[start] = str[end];
            str[end] = temp;
            start++;
            end--;
        }
        return String.valueOf(str);
    }
 
    // Function to convert infix to postfix expression
    static
                        String infixToPostfix(char[] infix1)
    {
        String infix = '(' + String.valueOf(infix1) + ')';
 
        int l = infix.length();
        Stack<Character> char_stack = new
                        Stack<>();
        String output = "";
 
        for (int i = 0; i < l; i++) {
 
            // If the scanned character is an
            // operand, add it to output.
            if (isalpha(infix.charAt(i))
                || isdigit(infix.charAt(i)))
                output += infix.charAt(i);
 
            // If the scanned character is an
            // ‘(‘, push it to the stack.
            else if (infix.charAt(i) == '(')
                char_stack.add('(');
 
            // If the scanned character is an
            // ‘)’, pop and output from the stack
            // until an ‘(‘ is encountered.
            else if (infix.charAt(i) == ')') {
                while (char_stack.peek() != '(') {
                    output += char_stack.peek();
                    char_stack.pop();
                }
 
                // Remove '(' from the stack
                char_stack.pop();
            }
 
            // Operator found
            else {
                if (isOperator(char_stack.peek())) {
                    while (
                        (getPriority(infix.charAt(i))
                         < getPriority(char_stack.peek()))
                        || (getPriority(infix.charAt(i))
                                <= getPriority(
                                    char_stack.peek())
                            && infix.charAt(i) == '^')) {
                        output += char_stack.peek();
                        char_stack.pop();
                    }
 
                    // Push current Operator on stack
                    char_stack.add(infix.charAt(i));
                }
            }
        }
        while (!char_stack.empty()) {
            output += char_stack.pop();
        }
        return output;
    }
 
    static
                        String infixToPrefix(char[] infix)
    {
        // Reverse String and replace ( with ) and vice
        // versa Get Postfix Reverse Postfix
        int l = infix.length;
 
        // Reverse infix
        String infix1 = reverse(infix, 0, l - 1);
        infix = infix1.toCharArray();
 
        // Replace ( with ) and vice versa
        for (int i = 0; i < l; i++) {
 
            if (infix[i] == '(') {
                infix[i] = ')';
                      
                i++;
            }
            else if (infix[i] == ')') {
                infix[i] = '(';
                      
                i++;
            }
        }
 
        String prefix = infixToPostfix(infix);
 
        // Reverse postfix
        prefix = reverse(prefix.toCharArray(), 0, l - 1);
 
        return prefix;
    }
 
    // Driver code
    public
                        static void main(String[] args)
    {
        String s = ("x+y*z/w+u");
 
        // Function call
        System.out.print(infixToPrefix(s.toCharArray()));
    }
}
 
// This code is contributed by Rajput-Ji

                

            
          

Python3

            
              
                  # Python code to convert infix to prefix expression
 
 
# Function to check if the character is an operator
def isOperator(c):
    return
                        (not c.isalpha()) and (not c.isdigit())
                      
 
 
 
# Function to get the priority of operators
def getPriority(c):
    if c == '-' or c == '+':
        return 1
    elif
                        c == '*' or c == '/':
        return 2
    elif
                        c == '^':
        return 3
    return
                        0
 
 
   
                      
# Function to convert the infix expression to postfix
def infixToPostfix(infix):
    infix = '(' + infix + ')'
                      
    l = len(infix)
                      
    char_stack = []
                      
    output = ""
 
    for i in range(l):
         
        # Check if the character is alphabet or digit
        if infix[i].isalpha() or infix[i].isdigit():
            output += infix[i]
             
                      
        # If the character is '(' push it in the stack
        elif infix[i] == '(':
            char_stack.append(infix[i])
         
        # If the character is ')' pop from the stack
        elif infix[i] == ')':
            while char_stack[-1] != '(':
                output += char_stack.pop()
            char_stack.pop()
         
        # Found an operator
        else:
            if isOperator(char_stack[-1]):
                if infix[i] == '^':
                    while getPriority(infix[i]) <= getPriority(char_stack[-1]):
                        output += char_stack.pop()
                else:
                    while getPriority(infix[i]) < getPriority(char_stack[-1]):
                        output += char_stack.pop()
                char_stack.append(infix[i])
 
    while
                        len(char_stack) != 0:
        output += char_stack.pop()
    return
                        output
 
 
 
# Function to convert infix expression to prefix
def infixToPrefix(infix):
    l = len(infix)
                      
 
    infix = infix[::-1]
 
    for i in range(l):
        if infix[i] == '(':
            infix[i] = ')'
                      
        elif infix[i] == ')':
            infix[i] = '('
                      
 
    prefix = infixToPostfix(infix)
    prefix = prefix[::-1]
 
    return
                        prefix
 
 
 
# Driver code
if __name__ ==
                        '__main__':
    s = "x+y*z/w+u"
     
    # Function call
    print(infixToPrefix(s))

                

            
          

C#

            
              
                  // C# program to convert infix to prefix
using System;
using System.Collections.Generic;
 
public class GFG {
    // Check if the given character is an alphabet
    static
                        bool isalpha(char c)
    {
        if (c >= 'a'
                        && c <= 'z' || c >= 'A' && c <= 'Z') {
            return true;
                      
        }
        return false;
                      
    }
 
    // Check if the current character is a digit
    static
                        bool isdigit(char c)
    {
        if (c >= '0'
                        && c <= '9') {
            return true;
                      
        }
        return false;
                      
    }
 
    // Function to check if the character is an operator
    static
                        bool isOperator(char c)
    {
        return (!isalpha(c) && !isdigit(c));
                      
    }
 
    // Function to get the precedence order of operators
    static
                        int getPriority(char C)
    {
        if (C == '-'
                        || C == '+')
                      
            return 1;
        else if (C == '*' || C == '/')
            return 2;
        else if (C == '^')
            return 3;
 
        return 0;
    }
 
    // Reverse the letters of the word
    static
                        String reverse(char[] str, int start, int end)
                      
    {
 
        // Temporary variable to store character
        char temp;
        while (start < end) {
 
            // Swapping the first and last character
            temp = str[start];
            str[start] = str[end];
            str[end] = temp;
            start++;
            end--;
        }
        return String.Join("", str);
    }
 
    // Function to convert infix to postfix notation
    static
                        String infixToPostfix(char[] infix1)
    {
        String infix = '(' + String.Join("", infix1) + ')';
                      
 
        int l = infix.Length;
        Stack<char> char_stack = new Stack<char>();
        String output = "";
 
        for (int i = 0; i < l; i++) {
 
            // If the scanned character is an
            // operand, add it to output.
            if (isalpha(infix[i]) || isdigit(infix[i]))
                      
                output += infix[i];
 
            // If the scanned character is an
            // ‘(‘, push it to the stack.
            else if (infix[i] == '(')
                      
                char_stack.Push('(');
 
            // If the scanned character is an
            // ‘)’, pop and output from the stack
            // until an ‘(‘ is encountered.
            else if (infix[i] == ')') {
                while (char_stack.Peek() != '(') {
                    output += char_stack.Peek();
                    char_stack.Pop();
                }
 
                // Remove '(' from the stack
                char_stack.Pop();
            }
 
            // Operator found
            else {
                if (isOperator(char_stack.Peek())) {
                    while (
                        (getPriority(infix[i])
                         < getPriority(char_stack.Peek()))
                        || (getPriority(infix[i])
                                <= getPriority(
                                    char_stack.Peek())
                            && infix[i] == '^')) {
                        output += char_stack.Peek();
                        char_stack.Pop();
                    }
 
                    // Push current Operator on stack
                    char_stack.Push(infix[i]);
                }
            }
        }
        while (char_stack.Count != 0) {
            output += char_stack.Pop();
        }
        return output;
    }
 
    // Driver code
    static
                        String infixToPrefix(char[] infix)
    {
        // Reverse String Replace ( with ) and vice versa
        // Get Postfix
        // Reverse Postfix *
        int l = infix.Length;
 
        // Reverse infix
        String infix1 = reverse(infix, 0, l - 1);
        infix = infix1.ToCharArray();
 
        // Replace ( with ) and vice versa
        for (int i = 0; i < l; i++) {
            if (infix[i] == '(') {
                infix[i] = ')';
                      
                i++;
            }
            else if (infix[i] == ')') {
                infix[i] = '(';
                      
                i++;
            }
        }
        String prefix = infixToPostfix(infix);
 
        // Reverse postfix
        prefix = reverse(prefix.ToCharArray(), 0, l - 1);
 
        return prefix;
    }
 
    // Driver code
    public
                        static void Main(String[] args)
    {
        String s = ("x+y*z/w+u");
       
        // Function call
        Console.Write(infixToPrefix(s.ToCharArray()));
    }
}
 
// This code is contributed by gauravrajput1

                

            
          

Javascript

            
              
                  // Javascript program to convert infix to prefix
// program to implement stack data structure
class Stack {
  constructor() {
    this.items = [];
  }
 
  // add element to the stack
  push(element) {
    return
                        this.items.push(element);
  }
 
  // remove element from the stack
  pop() {
    if (this.items.length > 0) {
      return this.items.pop();
    }
  }
 
  // view the last element
  top() {
    return
                        this.items[this.items.length - 1];
  }
 
  // check if the stack is empty
  isEmpty() {
    return
                        this.items.length == 0;
  }
 
  // the size of the stack
  size() {
    return
                        this.items.length;
  }
 
  // empty the stack
  clear() {
    this.items = [];
  }
}
 
function isalpha(c) {
  if ((c >= "a"
                        && c <= "z") || (c >= "A" && c <= "Z")) {
    return
                        true;
  }
  return false;
                      
}
 
function isdigit(c) {
  if (c >= "0"
                        && c <= "9") {
    return
                        true;
  }
  return false;
                      
}
function isOperator(c) {
  return !isalpha(c) && !isdigit(c);
                      
}
 
function getPriority(C) {
  if (C == "-"
                        || C == "+") return 1;
  else if (C == "*" || C == "/") return 2;
  else if (C == "^") return 3;
  return 0;
}
 
function infixToPostfix(infix) {
  infix = "(" + infix + ")";
                      
 
  var l = infix.length;
  let char_stack = new Stack();
  var output = "";
 
  for (var i = 0; i < l; i++) {
    // If the scanned character is an
    // operand, add it to output.
    if (isalpha(infix[i]) || isdigit(infix[i])) output += infix[i];
    // If the scanned character is an
    // ‘(‘, push it to the stack.
    else
                        if (infix[i] == "(") char_stack.push("(");
    // If the scanned character is an
    // ‘)’, pop and output from the stack
    // until an ‘(‘ is encountered.
    else
                        if (infix[i] == ")") {
      while (char_stack.top() != "(") {
        output += char_stack.top();
        char_stack.pop();
      }
 
      // Remove '(' from the stack
      char_stack.pop();
    }
 
    // Operator found
    else
                        {
      if (isOperator(char_stack.top())) {
        if (infix[i] == "^") {
          while (getPriority(infix[i]) <= getPriority(char_stack.top())) {
            output += char_stack.top();
            char_stack.pop();
          }
        } else {
          while (getPriority(infix[i]) < getPriority(char_stack.top())) {
            output += char_stack.top();
            char_stack.pop();
          }
        }
 
        // Push current Operator on stack
        char_stack.push(infix[i]);
      }
    }
  }
  while (!char_stack.isEmpty()) {
    output += char_stack.top();
    char_stack.pop();
  }
 
  return output;
}
 
function infixToPrefix(infix) {
  /* Reverse String
   * Replace ( with ) and vice versa
   * Get Postfix
                      
   * Reverse Postfix  *  */
  var l = infix.length;
 
  // Reverse infix
  infix = infix.split("").reverse().join("");
 
  // Replace ( with ) and vice versa
  var infixx = infix.split("");
  for (var i = 0; i < l; i++) {
    if (infixx[i] == "(") {
      infixx[i] = ")";
                      
    } else if (infixx[i] == ")") {
      infixx[i] = "(";
                      
    }
  }
  infix = infixx.join("");
 
  var prefix = infixToPostfix(infix);
 
  // Reverse postfix
  prefix = prefix.split("").reverse().join("");
  return prefix;
}
 
// Driver code
 
var s = "x+y*z/w+u";
                      
console.log(infixToPrefix(s));

                

            
          

输出

++x/*yzwu

复杂度分析：

时间复杂度： O(n)
- 像push()和pop()这样的堆栈操作是在恒定时间内执行的。
- 因为一旦复杂度随时间呈线性关系，我们就会扫描表达式中的所有字符
辅助空间 ：O(n)，因为我们要保留一个堆栈。

栈-表达式计算-顺序表 可视化交互式动画版

为什么用后缀表示表达式？

如何将中缀表达式转换为后缀表达式？

插图：

C++14

C

Java

Python3

C#

Javascript

如何将中缀表达式转换为前缀表达式？

C++

Java

Python3

C#

Javascript

栈-表达式计算-顺序表可视化交互式动画版