Floyd(弗洛伊德)算法可视化交互式动画版

Floyd -Warshall 算法 以其创始人 Robert Floyd 和 Stephen Warshall 命名，是计算机科学和图论中的基本算法。它用于查找加权图中所有节点对之间的最短路径。该算法非常高效，可以处理具有正边权重和 负边权重的 图，使其成为解决各种网络和连接问题的多功能工具。

弗洛伊德·沃歇尔(Floyd-Warshall)算法：

Floyd Warshall 算法 是全对最短路径算法，与单源最短路径算法 Dijkstra 和 Bellman Ford 不同。该算法适用于有向和 无向加权 图。但是，它不适用于具有负循环的图（其中循环中的边的总和为负）。它遵循动态规划方法来检查经过每个可能节点的每条可能路径，以计算每对节点之间的最短距离。

Floyd Warshall 算法背后的想法：

假设我们有一个图 G[][] ，其中 V 个 顶点从 1 到 N 。现在我们必须评估 shortestPathMatrix[][] ，其中 s hortestPathMatrix[i][j]表示顶点 i 和 j 之间的最短路径。

显然， i 到 j 之间的最短路径将有 k 个中间节点。 Floyd Warshall 算法背后的思想是将1 到 N 中的每个顶点逐一视为中间节点。

下图展示了上述floyd warshall算法中的最优子结构性质：

算法：

第一步，初始化与输入图矩阵相同的解矩阵。
然后通过将所有顶点视为中间顶点来更新解矩阵。
这个想法是一一挑选所有顶点并更新所有最短路径，其中包括作为最短路径中的中间顶点的挑选顶点。
当我们选择顶点编号 k 作为中间顶点时，我们已经将顶点 {0, 1, 2, .. k-1} 视为中间顶点。
对于每对 (i, j) 源顶点和目标顶点，有两种可能的情况。
- k 不是从 i 到 j 的最短路径中的中间顶点。 我们保持dist[i][j] 的值不变。
- k是从 i 到 j 的 最短路径中的中间顶点。 我们将dist[i][j] 的值更新为 dist[i][k] + dist[k][j]， 如果 dist[i][j] > dist[i][k] + dist[k] [j]

伪代码：

对于 k = 0 到 n – 1
对于 i = 0 到 n – 1
对于 j = 0 到 n – 1
距离[i, j] = min(距离[i, j], 距离[i, k] + 距离[k , j])

其中 i = 源节点，j = 目标节点，k = 中间节点

插图：

假设我们有一个如图所示的图：

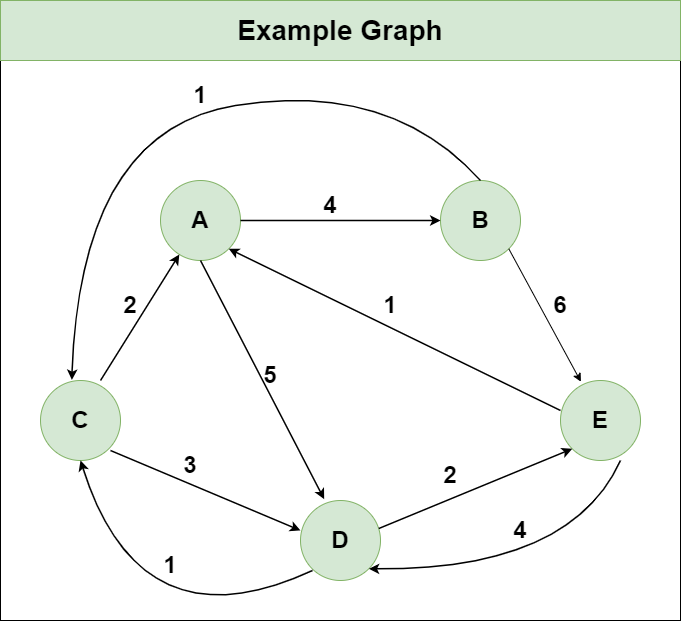
步骤 1 ：使用输入图初始化 Distance[][] 矩阵，使得 Distance[i][j]= 从 i 到 j 的边的权重，如果从 i 没有边，则 Distance[i][j] = Infinity 到 j。

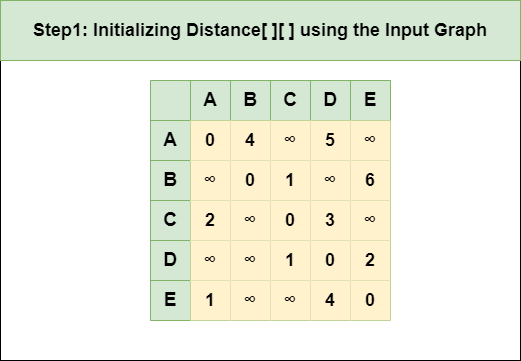
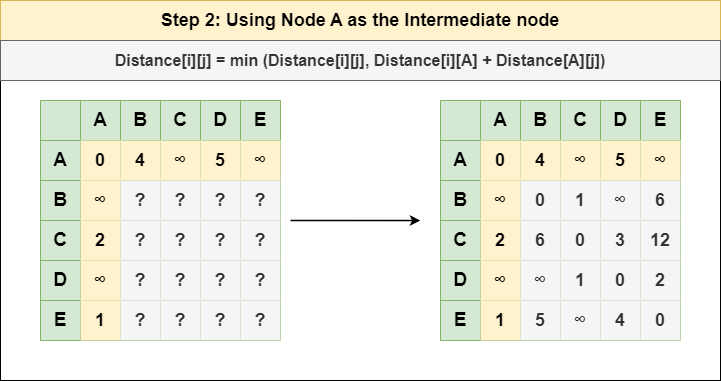
步骤 2 ：将节点 A 视为中间节点，并使用以下公式计算每个 {i,j} 节点对的 Distance[][]：

= 距离[i][j] = 最小值 (距离[i][j], (从 i 到 A 的距离) + (从 A 到 j 的距离 )) = 距离[i][j] = 最小值 (距离[i] [j], 距离[i][ A ] + 距离[ A ][j])

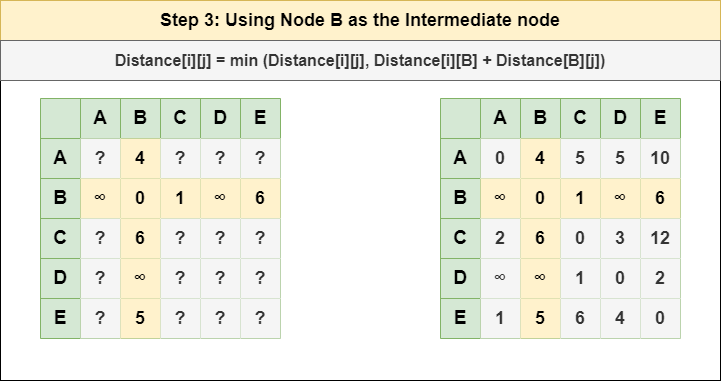
步骤 3 ：将节点 B 视为中间节点，并使用以下公式计算每个 {i,j} 节点对的 Distance[][]：

= 距离[i][j] = 最小值 (距离[i][j], (从 i 到 B 的距离) + (从 B 到 j 的距离 )) = 距离[i][j] = 最小值 (距离[i] [j], 距离[i][ B ] + 距离[ B ][j])

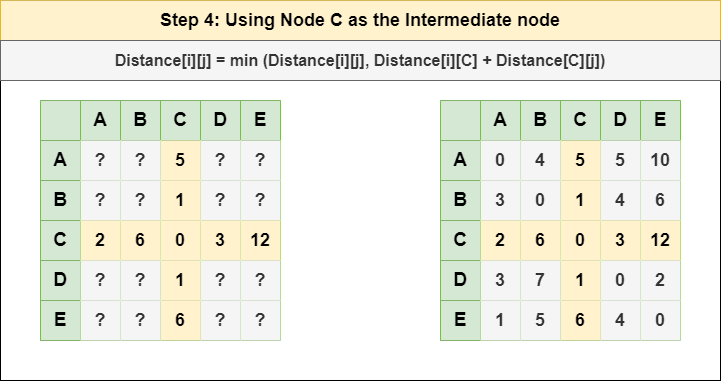
步骤 4 ：将节点 C 视为中间节点，并使用以下公式计算每个 {i,j} 节点对的 Distance[][]：

= 距离[i][j] = 最小值 (距离[i][j], (从 i 到 C 的距离) + (从 C 到 j 的距离 )) = 距离[i][j] = 最小值 (距离[i] [j], 距离[i][ C ] + 距离[ C ][j])

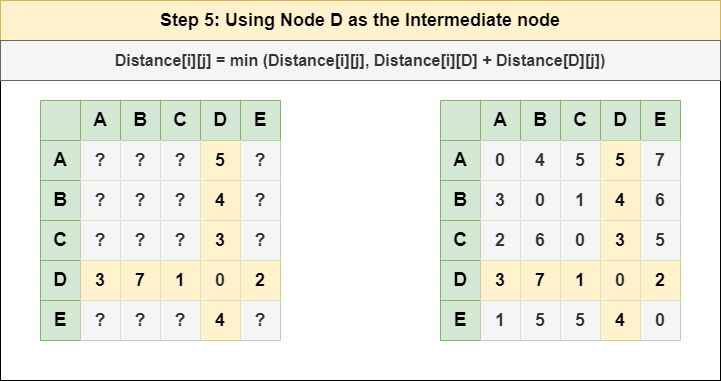
步骤 5 ：将节点 D 视为中间节点，并使用以下公式计算每个 {i,j} 节点对的 Distance[][]：

= 距离[i][j] = 最小值 (距离[i][j], (从 i 到 D 的距离) + (从 D 到 j 的距离 )) = 距离[i][j] = 最小值 (距离[i] [j], 距离[i][ D ] + 距离[ D ][j])

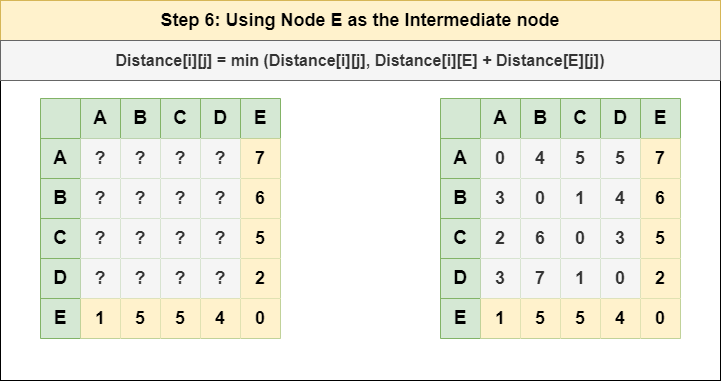
步骤 6 ：将节点 E 视为中间节点，并使用以下公式计算每个 {i,j} 节点对的 Distance[][]：

= 距离[i][j] = 最小值 (距离[i][j], (从 i 到 E 的距离) + (从 E 到 j 的距离 )) = 距离[i][j] = 最小值 (距离[i] [j], 距离[i][ E ] + 距离[ E ][j])

步骤7 ：由于所有节点都被视为中间节点，我们现在可以返回更新后的Distance[][]矩阵作为我们的答案矩阵。

下面是上述方法的实现：

C++

              
                
                    // C++ Program for Floyd Warshall Algorithm
#include <bits/stdc++.h>
using namespace std;
 
// Number of vertices in the graph
#define V 4
 
/* Define Infinite as a large enough
value.This value will be used for
vertices not connected to each other */
#define INF 99999
                        
 
// A function to print the solution matrix
void printSolution(int dist[][V]);
 
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(int dist[][V])
{
 
    int
                          i, j, k;
 
    /* Add all vertices one by one to
    the set of intermediate vertices.
    ---> Before start of an iteration,
    we have shortest distances between all
    pairs of vertices such that the
    shortest distances consider only the
    vertices in set {0, 1, 2, .. k-1} as
    intermediate vertices.
    ----> After the end of an iteration,
    vertex no. k is added to the set of
    intermediate vertices and the set becomes {0, 1, 2, ..
    k} */
                        
    for (k = 0; k < V; k++) {
        // Pick all vertices as source one by one
        for (i = 0; i < V; i++) {
            // Pick all vertices as destination for the
            // above picked source
            for (j = 0; j < V; j++) {
                // If vertex k is on the shortest path from
                // i to j, then update the value of
                // dist[i][j]
                if (dist[i][j] > (dist[i][k] + dist[k][j])
                    && (dist[k][j] != INF
                        && dist[i][k] != INF))
                    dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }
 
    // Print the shortest distance matrix
    printSolution(dist);
}
 
/* A utility function to print solution */
void printSolution(int dist[][V])
{
    cout << "The following matrix shows the shortest "
            "distances"
            " between every pair of vertices \n";
    for (int i = 0; i < V; i++) {
        for (int j = 0; j < V; j++) {
            if (dist[i][j] == INF)
                cout << "INF"
                     << " ";
                        
            else
                cout << dist[i][j] << "   ";
        }
        cout << endl;
    }
}
 
// Driver's code
int main()
{
    /* Let us create the following weighted graph
            10
    (0)------->(3)
        |     /|\
    5 |     |
        |     | 1
    \|/     |
    (1)------->(2)
            3     */
    int
                          graph[V][V] = { { 0, 5, INF, 10 },
                        { INF, 0, 3, INF },
                        { INF, INF, 0, 1 },
                        { INF, INF, INF, 0 } };
 
    // Function call
    floydWarshall(graph);
    return 0;
}
 
// This code is contributed by Mythri J L

                  

              
            

C

              
                
                    // C Program for Floyd Warshall Algorithm
#include <stdio.h>
                        
 
// Number of vertices in the graph
#define V 4
 
/* Define Infinite as a large enough
  value. This value will be used
  for vertices not connected to each other */
#define INF 99999
 
// A function to print the solution matrix
void printSolution(int dist[][V]);
 
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(int dist[][V])
{
    int
                          i, j, k;
 
    /* Add all vertices one by one to
      the set of intermediate vertices.
      ---> Before start of an iteration, we
      have shortest distances between all
      pairs of vertices such that the shortest
      distances consider only the
      vertices in set {0, 1, 2, .. k-1} as
      intermediate vertices.
      ----> After the end of an iteration,
      vertex no. k is added to the set of
      intermediate vertices and the set
      becomes {0, 1, 2, .. k} */
    for (k = 0; k < V; k++) {
        // Pick all vertices as source one by one
        for (i = 0; i < V; i++) {
            // Pick all vertices as destination for the
            // above picked source
            for (j = 0; j < V; j++) {
                // If vertex k is on the shortest path from
                // i to j, then update the value of
                // dist[i][j]
                if (dist[i][k] + dist[k][j] < dist[i][j])
                    dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }
 
    // Print the shortest distance matrix
    printSolution(dist);
}
 
/* A utility function to print solution */
void printSolution(int dist[][V])
{
    printf(
        "The following matrix shows the shortest distances"
        " between every pair of vertices \n");
                        
    for (int i = 0; i < V; i++) {
        for (int j = 0; j < V; j++) {
            if (dist[i][j] == INF)
                printf("%7s", "INF");
            else
                printf("%7d", dist[i][j]);
        }
        printf("\n");
    }
}
 
// driver's code
int main()
{
    /* Let us create the following weighted graph
            10
       (0)------->(3)
        |         /|\
      5 |          |
        |          | 1
       \|/         |
       (1)------->(2)
            3           */
                        
    int
                          graph[V][V] = { { 0, 5, INF, 10 },
                        { INF, 0, 3, INF },
                        { INF, INF, 0, 1 },
                        { INF, INF, INF, 0 } };
 
    // Function call
    floydWarshall(graph);
    return 0;
}

                  

              
            

Java

              
                
                    // Java program for Floyd Warshall All Pairs Shortest
// Path algorithm.
import java.io.*;
import java.lang.*;
import java.util.*;
 
class AllPairShortestPath {
    final
                          static int INF = 99999, V = 4;
 
    void
                          floydWarshall(int dist[][])
    {
 
        int i, j, k;
 
        /* Add all vertices one by one
           to the set of intermediate
           vertices.
          ---> Before start of an iteration,
               we have shortest
               distances between all pairs
               of vertices such that
               the shortest distances consider
               only the vertices in
               set {0, 1, 2, .. k-1} as
               intermediate vertices.
          ----> After the end of an iteration,
                vertex no. k is added
                to the set of intermediate
                vertices and the set
                becomes {0, 1, 2, .. k} */
        for (k = 0; k < V; k++) {
            // Pick all vertices as source one by one
            for (i = 0; i < V; i++) {
                // Pick all vertices as destination for the
                // above picked source
                for (j = 0; j < V; j++) {
                    // If vertex k is on the shortest path
                    // from i to j, then update the value of
                    // dist[i][j]
                    if (dist[i][k] + dist[k][j]
                        < dist[i][j])
                        dist[i][j]
                            = dist[i][k] + dist[k][j];
                }
            }
        }
 
        // Print the shortest distance matrix
        printSolution(dist);
    }
 
    void
                          printSolution(int dist[][])
    {
        System.out.println(
            "The following matrix shows the shortest "
            + "distances between every pair of vertices");
        for (int
                          i = 0; i < V; ++i) {
            for (int
                          j = 0; j < V; ++j) {
                if (dist[i][j] == INF)
                    System.out.print("INF ");
                else
                    System.out.print(dist[i][j] + "   ");
            }
            System.out.println();
        }
    }
 
    // Driver's code
    public
                          static void main(String[] args)
    {
        /* Let us create the following weighted graph
           10
        (0)------->(3)
        |         /|\
        5 |          |
        |          | 1
        \|/         |
        (1)------->(2)
           3           */
                        
        int graph[][] = { { 0, 5, INF, 10 },
                        
                          { INF, 0, 3, INF },
                          { INF, INF, 0, 1 },
                          { INF, INF, INF, 0 } };
        AllPairShortestPath a = new AllPairShortestPath();
 
        // Function call
        a.floydWarshall(graph);
    }
}
 
// Contributed by Aakash Hasija

                  

              
            

Python3

              
                
                    # Python3 Program for Floyd Warshall Algorithm
 
# Number of vertices in the graph
V = 4
 
# Define infinity as the large
# enough value. This value will be
# used for vertices not connected to each other
INF = 99999
 
# Solves all pair shortest path
# via Floyd Warshall Algorithm
 
 
def floydWarshall(graph):
    """ dist[][] will be the output 
       matrix that will finally
        have the shortest distances 
        between every pair of vertices """
    """ initializing the solution matrix 
    same as input graph matrix
    OR we can say that the initial 
    values of shortest distances
    are based on shortest paths considering no 
    intermediate vertices """
 
    dist = list(map(lambda
                          i: list(map(lambda j: j, i)), graph))
 
    """ Add all vertices one by one 
    to the set of intermediate
     vertices.
     ---> Before start of an iteration, 
     we have shortest distances
     between all pairs of vertices 
     such that the shortest
     distances consider only the 
     vertices in the set 
    {0, 1, 2, .. k-1} as intermediate vertices.
      ----> After the end of a 
      iteration, vertex no. k is
     added to the set of intermediate 
     vertices and the 
    set becomes {0, 1, 2, .. k}
    """
                        
    for
                          k in range(V):
 
        # pick all vertices as source one by one
        for i in
                          range(V):
 
            # Pick all vertices as destination for the
            # above picked source
            for j in
                          range(V):
 
                # If vertex k is on the shortest path from
                # i to j, then update the value of dist[i][j]
                dist[i][j] = min(dist[i][j],
                                 dist[i][k] + dist[k][j]
                                 )
    printSolution(dist)
 
 
# A utility function to print the solution
def printSolution(dist):
    print("Following matrix shows the shortest distances\
 between every pair of vertices")
    for
                          i in range(V):
        for j in
                          range(V):
            if(dist[i][j] == INF):
                        
                print("%7s"
                          % ("INF"), end=" ")
            else:
                print("%7d\t"
                          % (dist[i][j]), end=' ')
            if j == V-1:
                print()
 
 
# Driver's code
if __name__ ==
                          "__main__":
    """
                        
                10
           (0)------->(3)
            |         /|\
          5 |          |
            |          | 1
           \|/         |
           (1)------->(2)
                3           """
                        
    graph = [[0, 5, INF, 10],
             [INF, 0, 3, INF],
             [INF, INF, 0,   1],
                        
             [INF, INF, INF, 0]
             ]
    # Function call
    floydWarshall(graph)
# This code is contributed by Mythri J L

                  

              
            

C#

              
                
                    // C# program for Floyd Warshall All
// Pairs Shortest Path algorithm.
 
using System;
 
public class AllPairShortestPath {
    readonly static int INF = 99999, V = 4;
 
    void
                          floydWarshall(int[, ] graph)
    {
        int[, ] dist = new int[V, V];
        int i, j, k;
 
        // Initialize the solution matrix
        // same as input graph matrix
        // Or we can say the initial
        // values of shortest distances
        // are based on shortest paths
        // considering no intermediate
        // vertex
        for (i = 0; i < V; i++) {
            for (j = 0; j < V; j++) {
                dist[i, j] = graph[i, j];
            }
        }
 
        /* Add all vertices one by one to
        the set of intermediate vertices.
        ---> Before start of a iteration,
             we have shortest distances
             between all pairs of vertices
             such that the shortest distances
             consider only the vertices in
             set {0, 1, 2, .. k-1} as
             intermediate vertices.
        ---> After the end of a iteration,
             vertex no. k is added
             to the set of intermediate
             vertices and the set
             becomes {0, 1, 2, .. k} */
        for (k = 0; k < V; k++) {
            // Pick all vertices as source
            // one by one
            for (i = 0; i < V; i++) {
                // Pick all vertices as destination
                // for the above picked source
                for (j = 0; j < V; j++) {
                    // If vertex k is on the shortest
                    // path from i to j, then update
                    // the value of dist[i][j]
                    if (dist[i, k] + dist[k, j]
                        < dist[i, j]) {
                        dist[i, j]
                            = dist[i, k] + dist[k, j];
                    }
                }
            }
        }
 
        // Print the shortest distance matrix
        printSolution(dist);
    }
 
    void
                          printSolution(int[, ] dist)
    {
        Console.WriteLine(
            "Following matrix shows the shortest "
            + "distances between every pair of vertices");
        for (int
                          i = 0; i < V; ++i) {
            for (int
                          j = 0; j < V; ++j) {
                if (dist[i, j] == INF) {
                    Console.Write("INF ");
                }
                else {
                    Console.Write(dist[i, j] + " ");
                }
            }
 
            Console.WriteLine();
        }
    }
 
    // Driver's Code
    public
                          static void Main(string[] args)
    {
        /* Let us create the following
           weighted graph
              10
        (0)------->(3)
        |         /|\
        5 |         |
        |         | 1
        \|/         |
        (1)------->(2)
             3             */
                        
        int[, ] graph = { { 0, 5, INF, 10 },
                          { INF, 0, 3, INF },
                          { INF, INF, 0, 1 },
                          { INF, INF, INF, 0 } };
 
        AllPairShortestPath a = new AllPairShortestPath();
 
        // Function call
        a.floydWarshall(graph);
    }
}
 
// This article is contributed by
// Abdul Mateen Mohammed
                        

                  

              
            

Javascript

              
                
                    // A JavaScript program for Floyd Warshall All
      // Pairs Shortest Path algorithm.
 
      var INF = 99999;
      class AllPairShortestPath {
        constructor() {
          this.V = 4;
        }
 
        floydWarshall(graph) {
          var dist = Array.from(Array(this.V), () => new Array(this.V).fill(0));
          var i, j, k;
 
          // Initialize the solution matrix
          // same as input graph matrix
          // Or we can say the initial
          // values of shortest distances
          // are based on shortest paths
          // considering no intermediate
          // vertex
          for (i = 0; i < this.V; i++) {
            for (j = 0; j < this.V; j++) {
              dist[i][j] = graph[i][j];
            }
          }
 
          /* Add all vertices one by one to
        the set of intermediate vertices.
        ---> Before start of a iteration,
            we have shortest distances
            between all pairs of vertices
            such that the shortest distances
            consider only the vertices in
            set {0, 1, 2, .. k-1} as
            intermediate vertices.
        ---> After the end of a iteration,
            vertex no. k is added
            to the set of intermediate
            vertices and the set
            becomes {0, 1, 2, .. k} */
          for (k = 0; k < this.V; k++) {
            // Pick all vertices as source
            // one by one
            for (i = 0; i < this.V; i++) {
              // Pick all vertices as destination
              // for the above picked source
              for (j = 0; j < this.V; j++) {
                // If vertex k is on the shortest
                // path from i to j, then update
                // the value of dist[i][j]
                if (dist[i][k] + dist[k][j] < dist[i][j]) {
                  dist[i][j] = dist[i][k] + dist[k][j];
                }
              }
            }
          }
 
          // Print the shortest distance matrix
          this.printSolution(dist);
        }
 
        printSolution(dist) {
          document.write(
            "Following matrix shows the shortest " +
                        
              "distances between every pair of vertices<br>"
          );
          for (var
                          i = 0; i < this.V; ++i) {
            for (var
                          j = 0; j < this.V; ++j) {
              if (dist[i][j] == INF) {
                document.write(" INF ");
              } else {
                document.write("  " + dist[i][j] + " ");
              }
            }
 
            document.write("<br>");
          }
        }
      }
      // Driver Code
      /* Let us create the following
        weighted graph
            10
        (0)------->(3)
        |         /|\
        5 |         |
        |         | 1
        \|/         |
        (1)------->(2)
            3             */
                        
      var graph = [
        [0, 5, INF, 10],
        [INF, 0, 3, INF],
        [INF, INF, 0, 1],
        [INF, INF, INF, 0],
      ];
 
      var a = new
                          AllPairShortestPath();
 
      // Print the solution
      a.floydWarshall(graph);
       
      // This code is contributed by rdtaank.

                  

              
            

PHP

              
                
                    <?php
// PHP Program for Floyd Warshall Algorithm 
 
// Solves the all-pairs shortest path problem
// using Floyd Warshall algorithm 
function floydWarshall ($graph, $V, $INF) 
{ 
    /* dist[][] will be the output matrix 
    that will finally have the shortest 
    distances between every pair of vertices */
    $dist
                          = array(array(0,0,0,0),
                  array(0,0,0,0),
                  array(0,0,0,0),
                  array(0,0,0,0));
 
    /* Initialize the solution matrix same 
    as input graph matrix. Or we can say the 
    initial values of shortest distances are 
    based on shortest paths considering no 
    intermediate vertex. */
    for
                          ($i = 0; $i < $V; $i++) 
        for ($j
                          = 0; $j < $V; $j++) 
            $dist[$i][$j] = $graph[$i][$j]; 
 
    /* Add all vertices one by one to the set 
    of intermediate vertices. 
    ---> Before start of an iteration, we have 
    shortest distances between all pairs of 
    vertices such that the shortest distances 
    consider only the vertices in set 
    {0, 1, 2, .. k-1} as intermediate vertices. 
    ----> After the end of an iteration, vertex 
    no. k is added to the set of intermediate
    vertices and the set becomes {0, 1, 2, .. k} */
    for
                          ($k = 0; $k < $V; $k++) 
    { 
        // Pick all vertices as source one by one 
        for ($i
                          = 0; $i < $V; $i++) 
        { 
            // Pick all vertices as destination 
            // for the above picked source 
            for ($j
                          = 0; $j < $V; $j++) 
            { 
                // If vertex k is on the shortest path from 
                // i to j, then update the value of dist[i][j] 
                if ($dist[$i][$k] + $dist[$k][$j] < 
                                    $dist[$i][$j]) 
                    $dist[$i][$j] = $dist[$i][$k] +
                                    $dist[$k][$j]; 
            } 
        } 
    } 
 
    // Print the shortest distance matrix 
    printSolution($dist, $V, $INF); 
} 
 
/* A utility function to print solution */
function printSolution($dist, $V, $INF) 
{ 
    echo
                          "The following matrix shows the " .
                        
             "shortest distances between " . 
                "every pair of vertices \n"; 
    for
                          ($i = 0; $i < $V; $i++) 
    { 
        for ($j
                          = 0; $j < $V; $j++) 
        { 
            if ($dist[$i][$j] == $INF) 
                        
                echo "INF " ; 
            else
                echo $dist[$i][$j], " ";
        } 
        echo "\n"; 
                        
    } 
} 
 
// Drivers' Code
 
// Number of vertices in the graph 
$V = 4 ;
 
/* Define Infinite as a large enough 
value. This value will be used for
vertices not connected to each other */
$INF = 99999 ;
 
/* Let us create the following weighted graph 
        10 
(0)------->(3) 
    |     /|\ 
5 |     | 
    |     | 1 
\|/     | 
(1)------->(2) 
        3     */
$graph = array(array(0, 5, $INF, 10), 
               array($INF, 0, 3, $INF), 
               array($INF, $INF, 0, 1), 
               array($INF, $INF, $INF, 0)); 
 
// Function call
floydWarshall($graph, $V, $INF); 
 
// This code is contributed by Ryuga
?>

                  

              
            

输出

下面的矩阵显示了每对顶点之间的最短距离
0 5 8 9   
中导号 0 3 4   
中标 中标 0 1   
INF INF 0

复杂性分析 ：

时间复杂度： O(V ³ )，其中 V 是图中的顶点数，我们运行三个嵌套循环，每个循环的大小为 V
辅助空间： O(V ² )，创建一个二维矩阵，以存储每对节点的最短距离。

注意：上述程序仅打印最短距离。我们还可以通过将前驱信息存储在单独的二维矩阵中来修改解决方案以打印最短路径。

为什么 Floyd-Warshall 算法更适合密集图而不是稀疏图？

密集图 ：边数明显多于顶点数的图。
稀疏图 ：边数非常少的图。

无论图中有多少条边， Floyd Warshall 算法 都会运行 O(V ³ ) 次，因此它最适合 密集图 。在稀疏图的情况下， 约翰逊算法 更适合。

与弗洛伊德·沃歇尔(Floyd-Warshall)相关的重要面试问题：

如何使用 Floyd Warshall 算法检测图中的负循环？
Floyd-warshall 算法与 Dijkstra 算法有何不同？
Floyd-warshall 算法与 Bellman-Ford 算法有何不同？

Floyd-Warshall 算法的现实应用：

在计算机网络中，该算法可用于查找网络中所有节点对之间的最短路径。这称为 网络路由 。
航班连接在航空业中寻找机场之间的最短路径。
GIS （ 地理信息系统 ）应用通常涉及分析空间数据（例如道路网络），以找到位置之间的最短路径。
Kleene 算法是 Floyd Warshall 的推广，可用于查找正则语言的正则表达式。