Dijkstra(迪杰斯特拉)算法可视化交互式动画版

什么是 Dijkstra 算法？

Dijkstra算法是一种流行的算法，用于解决许多图中具有非负边权重的单源最短路径问题，即找到图上两个顶点之间的最短距离。 它是由荷兰计算机科学家Edsger W. Dijkstra 于 1956 年提出的。

该算法维护一组已访问的顶点和一组未访问的顶点。它从源顶点开始，迭代地选择距源具有最小暂定距离的未访问顶点。然后，它访问该顶点的邻居，如果找到更短的路径，则更新它们的暂定距离。这个过程一直持续到到达目的地顶点，或者所有可到达的顶点都被访问过。

什么是 Dijkstra 算法？
- Dijkstra 算法的需求（目的和用例）
Dijkstra 算法的基础知识
- 实施 Dijkstra 算法的基本要求
- Dijkstra 算法可以同时适用于有向图和无向图吗？
算法：
Dijkstra 算法如何工作？
Dijkstra 算法的伪代码
实施 Dijkstra 算法的方法
Dijkstra算法的实现：
- 1.使用priority_queue（堆）的Dijkstra最短路径算法
- 2. 使用Prim算法的Dijkstra最短路径算法
- 3. Dijkstra 边数最少的最短路径
- 4. Dijkstra使用Set的最短路径算法
Dijkstra算法的复杂度分析
Dijkstra 算法与其他算法
与 Dijkstra 算法相关的问题

需要 Dijkstra 算法（目的和用例）

在许多应用中都需要 Dijkstra 算法，其中找到两点之间的最短路径至关重要。

例如，它可以用在计算机网络的路由协议中，也可以被地图系统用来查找起点和目的地之间的最短路径（如 Google 地图如何工作？中所述）

Dijkstra算法的基本特征

以下是 Dijkstra 算法工作原理的基本步骤：

所以基本上，Dijkstra 算法从我们选择的节点源节点开始，然后分析图条件及其路径，以找到给定节点与图中所有其他节点之间的最佳最短距离。
Dijkstra 算法跟踪当前已知的从每个节点到源节点的最短距离，并在找到最佳路径后更新该值，一旦算法找到源节点和目标节点之间的最短路径，则将特定节点标记为已访问。

实施 Dijkstra 算法的基本要求

图： Dijkstra 算法可以在任何图上实现，但它最适合具有非负边权重的加权有向图，并且图应表示为一组顶点和边。
源顶点： Dijkstra 算法需要一个源节点作为搜索的起点。
目标顶点： Dijkstra 算法可以修改为一旦到达特定目标顶点就终止搜索。
非负边： Dijkstra 算法仅适用于具有正权重的图，这是因为在此过程中必须添加边的权重才能找到最短路径。如果图中存在负权重，则算法将无法正常工作。一旦节点被标记为已访问，到该节点的当前路径将被标记为到达该节点的最短路径。

Dijkstra 算法可以同时适用于有向图和无向图吗？

是的，Dijkstra 算法可以适用于有向图和无向图，因为该算法被设计为适用于任何类型的图，只要它满足具有非负边权重和连接的要求。

在有向图中， 每条边都有一个方向，表示边所连接的顶点之间的行进方向。在这种情况下，算法在搜索最短路径时遵循边缘的方向。
在无向图中， 边没有方向，算法在搜索最短路径时可以沿着边向前和向后遍历。

Dijkstra 算法的算法：

将当前距离标记为 0 的源节点，将其余节点标记为无穷大。
将当前距离最小的未访问节点设置为当前节点。
对于每个邻居，当前节点的N加上相邻节点的当前距离以及连接0->1的边的权重。如果小于Node当前距离，则将其设置为新的N当前距离。
将当前节点 1 标记为已访问。
如果还有未访问的节点，则转步骤2。

Dijkstra 算法是如何工作的？

让我们通过下面给出的示例来看看 Dijkstra 算法是如何工作的：

Dijkstra 算法将生成从节点 0 到图中所有其他节点的最短路径。

考虑下图：

迪杰斯特拉算法

该算法将生成从节点 0 到图中所有其他节点的最短路径。

对于该图，我们假设边的权重表示两个节点之间的距离。

我们可以看到，我们有从
节点 0 到节点 1、从
节点 0 到节点 2、从
节点 0 到节点 3、从
节点 0 到节点 4、从
节点 0 到节点 6 的最短路径。

最初我们有一组资源如下：

源节点到自身的距离为 0。在本例中，源节点为 0。

从源节点到所有其他节点的距离未知，因此我们将它们全部标记为无穷大。

示例：0 -> 0、1-> 无穷大、2-> 无穷大、3-> 无穷大、4-> 无穷大、5-> 无穷大、6-> 无穷大。

我们还将有一个未访问元素数组，用于跟踪未访问或未标记的节点。

当所有节点都标记为已访问并且它们之间的距离添加到路径中时，算法将完成。 未访问的节点：- 0 1 2 3 4 5 6。

第 1 步： 从节点 0 开始，将节点标记为已访问，如下图所示，已访问节点标记为红色。

迪杰斯特拉算法

步骤 2： 检查相邻节点，现在我们必须选择（选择距离为 2 的节点 1 或选择距离为 6 的节点 2）并选择距离最小的节点。在此步骤中， 节点 1 是相邻节点的最小距离，因此将其标记为已访问并添加距离。

距离：节点 0 -> 节点 1 = 2

迪杰斯特拉算法

步骤3： 然后向前移动并检查相邻节点，即节点3，因此将其标记为已访问并添加距离，现在距离将是：

距离：节点 0 -> 节点 1 -> 节点 3 = 2 + 5 = 7

迪杰斯特拉算法

步骤 4： 对于相邻节点，我们同样有两种选择（要么选择距离为 10 的节点 4，要么选择距离为 15 的节点 5），因此选择距离最小的节点。在此步骤中， 节点 4 是相邻节点的最小距离，因此将其标记为已访问并累加距离。

距离：节点 0 -> 节点 1 -> 节点 3 -> 节点 4 = 2 + 5 + 10 = 17

迪杰斯特拉算法

步骤 5： 再次向前移动并检查相邻节点，即 节点 6 ，因此将其标记为已访问并添加距离，现在距离将为：

距离：节点 0 -> 节点 1 -> 节点 3 -> 节点 4 -> 节点 6 = 2 + 5 + 10 + 2 = 19

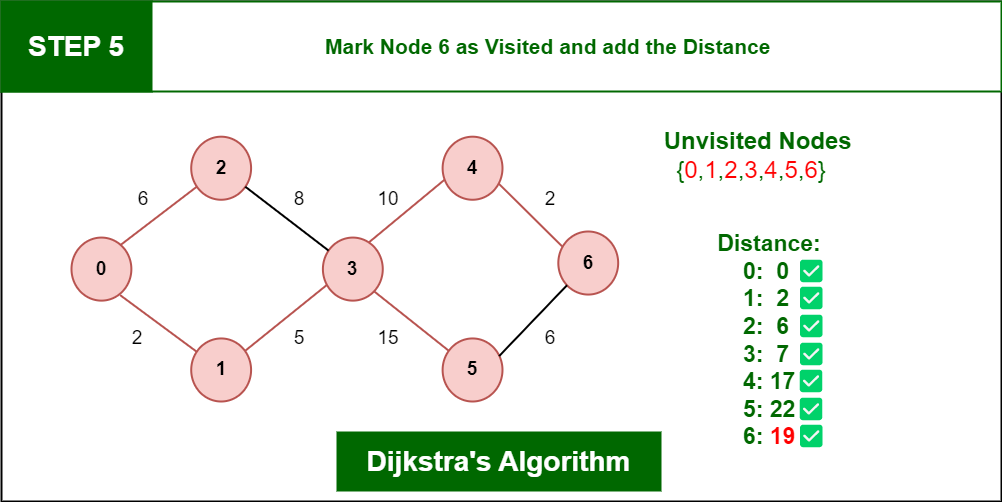
迪杰斯特拉算法

因此，距源顶点的最短距离是 19，这是最佳距离

Dijkstra 算法的伪代码

function Dijkstra(Graph, source):
// 将到所有节点的距离初始化为无穷大，源节点除外。 距离 = 将无穷远映射到所有节点 距离 = 0

// 初始化一组空的已访问节点和一个优先级队列来跟踪要访问的节点。
已访问=空集 队列=新的PriorityQueue（） queue.enqueue（源，0）


// 循环直到所有节点都被访问过。 whilequeue is notempty: // 将与优先级队列距离最小的节点出队。 当前=queue.dequeue()


// 如果该节点已经被访问过，则跳过它。 如果当前已访问： 继续


// 将节点标记为已访问。 访问过.add（当前）

// 检查所有邻居节点，看看它们的距离是否需要更新。 for neighbors in Graph.neighbors(current): // 计算通过当前节点到邻居的暂定距离。 tentative_distance = 距离[当前] + Graph.distance(当前，邻居)



// 如果暂定距离小于当前到邻居的距离，则更新距离。 如果暂定距离 < 距离[邻居]： 距离[邻居] = 暂定距离



// 将邻居的新距离加入队列，以便将来考虑访问。 queue.enqueue(邻居, 距离[邻居])

// 返回从源到图中所有其他节点的计算距离。 返回距离

实施 Dijkstra 算法的方法：

实现 Dijkstra 算法的方法有多种，但最常见的是：

使用 优先级队列 来跟踪所有顶点。
使用数组来跟踪距离。
使用集合来跟踪访问过的顶点。

1. 使用priority_queue（堆）的Dijkstra最短路径算法

在这个实现中，我们给定一个图和图中的源顶点，找到从源到给定图中所有顶点的最短路径。

例子：

输入： 源 = 0

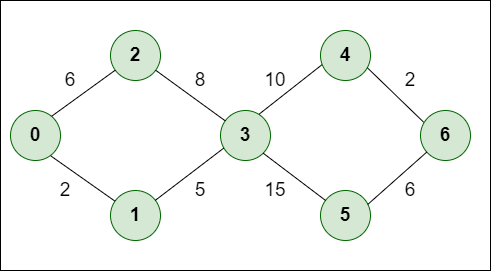
例子

输出： 顶点

距源的顶点距离

0 -> 0
1 -> 2
2 -> 6
3 -> 7
4 -> 17
5 -> 22
6 -> 19

下面是基于上述思想的算法：

将所有顶点的距离初始化为无限。
创建一个空的 priority_queue pq 。 pq 的每一项都是一对（权重、顶点）。重量（或距离）用作对的第一项，因为第一项默认用于比较两对
将源顶点插入到 pq 中，并使其距离为0。
虽然 pq 不会变空
1. 从 pq 中提取最小距离顶点。
  令提取的顶点为u。
2. 循环遍历 u 的所有相邻顶点，并对每个顶点 v 执行以下操作。
3. 如果有一条通过 u 到 v 的更短路径。
  1. 更新v的距离，即dist[v] = dist[u] + Weight(u, v)
  2. 将 v 插入 pq （即使 v 已经存在）
打印距离数组 dist[] 以打印所有最短路径。

下面是上述方法的 C++ 实现：

C++
Java
Python3
C＃
JavaScript

C++

              
                
                    // Program to find Dijkstra's shortest path using
// priority_queue in STL
                        
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
                        
 
// iPair ==> Integer Pair
                        
typedef pair<int, int> iPair;
 
// This class represents a directed graph using
// adjacency list representation
class Graph {
    int
                          V; // No. of vertices
 
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    list<pair<int, int> >* adj;
 
public:
    Graph(int V); // Constructor
 
    // function to add an edge to graph
    void addEdge(int u, int v, int w);
 
    // prints shortest path from s
    void shortestPath(int s);
};
 
// Allocates memory for adjacency list
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<iPair>[V];
}
 
void Graph::addEdge(int u, int v, int w)
                        
{
    adj[u].push_back(make_pair(v, w));
    adj[v].push_back(make_pair(u, w));
}
 
// Prints shortest paths from src to all other vertices
void Graph::shortestPath(int src)
{
    // Create a priority queue to store vertices that
    // are being preprocessed. This is weird syntax in C++.
    // Refer below link for details of this syntax
    // https://www.geeksforgeeks.org/implement-min-heap-using-stl/
                        
    priority_queue<iPair, vector<iPair>, greater<iPair> >
                        
        pq;
 
    // Create a vector for distances and initialize all
    // distances as infinite (INF)
    vector<int> dist(V, INF);
 
    // Insert source itself in priority queue and initialize
    // its distance as 0.
    pq.push(make_pair(0, src));
    dist[src] = 0;
 
    /* Looping till priority queue becomes empty (or all
    distances are not finalized) */
    while (!pq.empty()) {
        // The first vertex in pair is the minimum distance
        // vertex, extract it from priority queue.
        // vertex label is stored in second of pair (it
        // has to be done this way to keep the vertices
        // sorted distance (distance must be first item
        // in pair)
        int u = pq.top().second;
        pq.pop();
 
        // 'i' is used to get all adjacent vertices of a
        // vertex
        list<pair<int, int> >::iterator i;
        for (i = adj[u].begin(); i != adj[u].end(); ++i) {
            // Get vertex label and weight of current
            // adjacent of u.
            int v = (*i).first;
            int weight = (*i).second;
 
            // If there is shorted path to v through u.
            if (dist[v] > dist[u] + weight) {
                        
                // Updating distance of v
                dist[v] = dist[u] + weight;
                pq.push(make_pair(dist[v], v));
            }
        }
    }
 
    // Print shortest distances stored in dist[]
    printf("Vertex Distance from Source\n");
    for (int i = 0; i < V; ++i)
        printf("%d \t\t %d\n", i, dist[i]);
}
 
// Driver program to test methods of graph class
int main()
{
    // create the graph given in above figure
    int
                          V = 7;
    Graph g(V);
 
    // making above shown graph
    g.addEdge(0, 1, 2);
    g.addEdge(0, 2, 6);
    g.addEdge(1, 3, 5);
    g.addEdge(2, 3, 8);
    g.addEdge(3, 4, 10);
    g.addEdge(3, 5, 15);
    g.addEdge(4, 6, 2);
    g.addEdge(5, 6, 6);
    g.shortestPath(0);
 
    return 0;
}

                  

              
            

Java

              
                
                    import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.PriorityQueue;
 
public class DijkstraAlgoForShortestDistance {
                        
 
    static
                          class Node implements Comparable<Node> {
        int v;
        int distance;
 
        public Node(int v, int
                          distance)
        {
            this.v = v;
            this.distance = distance;
        }
 
        @Override public int compareTo(Node n)
        {
            if (this.distance <= n.distance) {
                return -1;
            }
            else {
                return 1;
            }
        }
    }
 
    static
                          int[] dijkstra(
        int V,
        ArrayList<ArrayList<ArrayList<Integer> > > adj,
        int S)
    {
        boolean[] visited = new boolean[V];
        HashMap<Integer, Node> map = new
                          HashMap<>();
        PriorityQueue<Node> q = new PriorityQueue<>();
 
        map.put(S, new Node(S, 0));
                        
        q.add(new Node(S, 0));
                        
 
        while (!q.isEmpty()) {
            Node n = q.poll();
            int v = n.v;
            int distance = n.distance;
            visited[v] = true;
 
            ArrayList<ArrayList<Integer> > adjList
                = adj.get(v);
            for (ArrayList<Integer> adjLink : adjList) {
 
                if (visited[adjLink.get(0)] == false) {
                    if (!map.containsKey(adjLink.get(0))) {
                        map.put(
                            adjLink.get(0),
                        
                            new Node(v,
                                     distance
                                         + adjLink.get(1)));
                    }
                    else {
                        Node sn = map.get(adjLink.get(0));
                        if (distance + adjLink.get(1)
                            < sn.distance) {
                            sn.v = v;
                            sn.distance
                                = distance + adjLink.get(1);
                        }
                    }
                    q.add(new Node(adjLink.get(0),
                                   distance
                                       + adjLink.get(1)));
                }
            }
        }
 
        int[] result = new int[V];
                        
        for (int
                          i = 0; i < V; i++) {
            result[i] = map.get(i).distance;
        }
 
        return result;
    }
 
    public
                          static void main(String[] args)
    {
        ArrayList<ArrayList<ArrayList<Integer> > > adj
            = new ArrayList<>();
        HashMap<Integer, ArrayList<ArrayList<Integer> > >
                        
            map = new HashMap<>();
 
        int V = 6;
        int E = 5;
        int[] u = { 0, 0, 1, 2, 4 };
        int[] v = { 3, 5, 4, 5, 5 };
        int[] w = { 9, 4, 4, 10, 3 };
 
        for (int
                          i = 0; i < E; i++) {
            ArrayList<Integer> edge = new ArrayList<>();
            edge.add(v[i]);
            edge.add(w[i]);
 
            ArrayList<ArrayList<Integer> > adjList;
            if (!map.containsKey(u[i])) {
                adjList = new ArrayList<>();
            }
            else {
                adjList = map.get(u[i]);
            }
            adjList.add(edge);
            map.put(u[i], adjList);
 
            ArrayList<Integer> edge2 = new ArrayList<>();
            edge2.add(u[i]);
            edge2.add(w[i]);
 
            ArrayList<ArrayList<Integer> > adjList2;
            if (!map.containsKey(v[i])) {
                adjList2 = new ArrayList<>();
            }
            else {
                adjList2 = map.get(v[i]);
            }
            adjList2.add(edge2);
            map.put(v[i], adjList2);
        }
 
        for (int
                          i = 0; i < V; i++) {
            if (map.containsKey(i)) {
                adj.add(map.get(i));
            }
            else {
                adj.add(null);
                        
            }
        }
        int S = 1;
 
        // Input sample
        //[0 [[3, 9], [5, 4]],
        // 1 [[4, 4]],
        // 2 [[5, 10]],
        // 3 [[0, 9]],
        // 4 [[1, 4], [5, 3]],
        // 5 [[0, 4], [2, 10], [4, 3]]
        //]
        int[] result
            = DijkstraAlgoForShortestDistance.dijkstra(
                V, adj, S);
        System.out.println(Arrays.toString(result));
    }
}

                  

              
            

Python3

              
                
                    # Python implementation of Dijkstra Algorithm
 
import heapq
 
class Node:
    def
                          __init__(self, v, distance):
        self.v = v
        self.distance = distance
 
    def
                          __lt__(self, other):
        return self.distance < other.distance
 
def dijkstra(V, adj, S):
    visited = [False] * V
    map
                          = {}
    q = []
 
    map[S] =
                          Node(S, 0)
                        
    heapq.heappush(q, Node(S, 0))
 
    while
                          q:
        n = heapq.heappop(q)
        v = n.v
        distance = n.distance
        visited[v] = True
 
        adjList = adj[v]
        for adjLink in adjList:
            if not visited[adjLink[0]]:
                if adjLink[0] not in map:
                        
                    map[adjLink[0]] = Node(v, distance + adjLink[1])
                else:
                    sn = map[adjLink[0]]
                    if distance +
                          adjLink[1] < sn.distance:
                        sn.v = v
                        sn.distance = distance + adjLink[1]
                heapq.heappush(q, Node(adjLink[0], distance + adjLink[1]))
                        
 
    result = [0] * V
    for
                          i in range(V):
        result[i] = map[i].distance
 
    return
                          result
 
def main():
    adj = [[] for
                          _ in range(6)]
 
    V = 6
    E = 5
    u = [0, 0, 1, 2, 4]
    v = [3, 5, 4, 5, 5]
    w = [9, 4, 4, 10, 3]
 
    for
                          i in range(E):
        edge = [v[i], w[i]]
        adj[u[i]].append(edge)
 
        edge2 = [u[i], w[i]]
        adj[v[i]].append(edge2)
 
    S = 1
 
    result = dijkstra(V, adj, S)
    print(result)
 
if __name__ ==
                          "__main__":
    main()
                        
 
# This code is contributed by ragul21

                  

              
            

C#

              
                
                    // C# Code:
using System;
using System.Collections.Generic;
 
public class Graph {
    // No. of vertices
    private
                          int V;
 
    // adjacency list
    private
                          List<Tuple<int, int> >[] adj;
 
    // Constructor
    public
                          Graph(int v)
    {
        V = v;
        adj = new List<Tuple<int, int> >[ v ];
        for (int
                          i = 0; i < v; ++i)
            adj[i] = new List<Tuple<int, int> >();
    }
 
    // function to add an edge to graph
    public
                          void addEdge(int u, int
                          v, int w)
                        
    {
        adj[u].Add(Tuple.Create(v, w));
        adj[v].Add(Tuple.Create(u, w));
    }
 
    // prints shortest path from s
    public
                          void shortestPath(int s)
    {
        // Create a priority queue to store vertices that
        // are being preprocessed.
        var pq = new
                          PriorityQueue<Tuple<int, int> >();
 
        // Create a vector for distances and initialize all
        // distances as infinite (INF)
        var dist = new int[V];
                        
        for (int
                          i = 0; i < V; i++)
            dist[i] = int.MaxValue;
 
        // Insert source itself in priority queue and
        // initialize its distance as 0.
        pq.Enqueue(Tuple.Create(0, s));
        dist[s] = 0;
 
        /* Looping till priority queue becomes empty (or all
        distances are not finalized) */
        while (pq.Count != 0) {
            // The first vertex in pair is the minimum
            // distance vertex, extract it from priority
            // queue. vertex label is stored in second of
            // pair (it has to be done this way to keep the
            // vertices sorted distance (distance must be
            // first item in pair)
            var u = pq.Dequeue().Item2;
 
            // 'i' is used to get all adjacent vertices of a
            // vertex
            foreach(var
                          i in adj[u])
            {
                // Get vertex label and weight of current
                // adjacent of u.
                int v = i.Item1;
                int weight = i.Item2;
 
                //  If there is shorted path to v through u.
                if (dist[v] > dist[u] + weight) {
                    // Updating distance of v
                    dist[v] = dist[u] + weight;
                    pq.Enqueue(Tuple.Create(dist[v], v));
                }
            }
        }
 
        // Print shortest distances stored in dist[]
        Console.WriteLine("Vertex Distance from Source");
        for (int
                          i = 0; i < V; ++i)
            Console.WriteLine("{0}\t\t{1}", i, dist[i]);
    }
}
 
public class PriorityQueue<T> {
    private
                          readonly List<T> _data;
    private
                          readonly Comparison<T> _compare;
                        
 
    public
                          PriorityQueue()
        : this(Comparer<T>.Default)
    {
    }
 
    public
                          PriorityQueue(IComparer<T> comparer)
        : this(comparer.Compare)
    {
    }
 
    public
                          PriorityQueue(Comparison<T> comparison)
    {
        _data = new List<T>();
        _compare = comparison;
    }
 
    public
                          void Enqueue(T item)
    {
        _data.Add(item);
        var childIndex = _data.Count - 1;
 
        while (childIndex > 0) {
            var parentIndex = (childIndex - 1) / 2;
                        
            if (_compare(_data[childIndex],
                         _data[parentIndex])
                >= 0)
                break;
 
            T tmp = _data[childIndex];
            _data[childIndex] = _data[parentIndex];
            _data[parentIndex] = tmp;
 
            childIndex = parentIndex;
        }
    }
 
    public
                          T Dequeue()
    {
        // assumes pq is not empty; up to calling code
        var lastElement = _data.Count - 1;
 
        var frontItem = _data[0];
        _data[0] = _data[lastElement];
        _data.RemoveAt(lastElement);
 
        --lastElement;
 
        var parentIndex = 0;
        while (true) {
            var childIndex = parentIndex * 2 + 1;
                        
            if (childIndex > lastElement)
                break; // End of tree
 
            var rightChild = childIndex + 1;
            if (rightChild <= lastElement
                && _compare(_data[rightChild],
                            _data[childIndex])
                       < 0)
                childIndex = rightChild;
 
            if (_compare(_data[parentIndex],
                         _data[childIndex])
                <= 0)
                break; // Correct position
 
            T tmp = _data[parentIndex];
            _data[parentIndex] = _data[childIndex];
            _data[childIndex] = tmp;
 
            parentIndex = childIndex;
        }
 
        return frontItem;
    }
 
    public
                          T Peek()
    {
        T frontItem = _data[0];
        return frontItem;
    }
 
    public
                          int Count
    {
        get { return
                          _data.Count; }
    }
}
 
class Program {
    // Driver program to test methods of graph class
    static
                          void Main(string[] args)
    {
        // create the graph given in above figure
        int V = 7;
        Graph g = new Graph(V);
 
        // making above shown graph
        g.addEdge(0, 1, 2);
        g.addEdge(0, 2, 6);
        g.addEdge(1, 3, 5);
        g.addEdge(2, 3, 8);
        g.addEdge(3, 4, 10);
        g.addEdge(3, 5, 15);
        g.addEdge(4, 6, 2);
        g.addEdge(5, 6, 6);
        g.shortestPath(0);
    }
}

                  

              
            

Javascript

              
                
                    class PriorityQueue {
    constructor() {
        this.queue = [];
    }
 
    enqueue(element, priority) {
        this.queue.push({ element, priority });
                        
        this.queue.sort((a, b) => a.priority - b.priority);
    }
 
    dequeue() {
        if (this.isEmpty()) {
            return null;
                        
        }
        return this.queue.shift().element;
    }
 
    isEmpty() {
        return this.queue.length === 0;
    }
}
 
class Graph {
    constructor(V) {
        this.V = V;
        this.adj = new Array(V);
        for (let i = 0; i < V; i++) {
            this.adj[i] = [];
        }
    }
 
    addEdge(u, v, w) {
        this.adj[u].push({ v, w });
        this.adj[v].push({ v: u, w });
    }
 
    shortestPath(src) {
        const pq = new PriorityQueue();
        const dist = new Array(this.V).fill(Infinity);
        const visited = new Array(this.V).fill(false);
 
        pq.enqueue(src, 0);
        dist[src] = 0;
 
        while (!pq.isEmpty()) {
            const u = pq.dequeue();
 
            if (visited[u]) continue;
            visited[u] = true;
 
            for (const { v, w } of this.adj[u]) {
                if (!visited[v] && dist[u] + w < dist[v]) {
                    dist[v] = dist[u] + w;
                    pq.enqueue(v, dist[v]);
                }
            }
        }
 
        console.log("Vertex Distance from Source");
        for (let i = 0; i < this.V; i++) {
            console.log(`${i}\t\t${dist[i] === Infinity ? "Infinity" : dist[i]}`);
        }
    }
}
 
function main() {
    const V = 7;
    const g = new Graph(V);
 
    g.addEdge(0, 1, 2);
    g.addEdge(0, 2, 6);
    g.addEdge(1, 3, 5);
    g.addEdge(2, 3, 8);
    g.addEdge(3, 4, 10);
    g.addEdge(3, 5, 15);
    g.addEdge(4, 6, 2);
    g.addEdge(5, 6, 6);
 
    g.shortestPath(0);
}
 
main();

                  

              
            

输出

最终答案：

输出

使用优先级队列的Dijkstra算法的复杂度分析：

时间复杂度：O(E log V)
空间复杂度：O(V ² )，这里V是顶点数。

2. 使用Prim算法的Dijkstra最短路径算法

给定一个图和图中的源顶点，找到从源到给定图中所有顶点的最短路径。

例子：

例子

输出： 0 2 6 7 17 22 19

请按照以下步骤使用 Prim 算法实现 Dijkstra 算法：

创建一个集合 sptSet （最短路径树集），用于跟踪最短路径树中包含的顶点，即计算并最终确定其到源的最小距离。最初，该集合是空的。
为输入图中的所有顶点分配距离值。将所有距离值初始化为 INFINITE 。将源顶点的距离值指定为 0 ，以便首先拾取它。
虽然 sptSet 不包含所有顶点
- 选择sptSet 中不存在且具有最小距离值的顶点 u。
- 将 u 包含到 sptSet 中。
- 然后更新u的所有相邻顶点的距离值。
  - 要更新距离值，请迭代所有相邻顶点。
  - 对于每个相邻顶点 v ，如果 u （距源）的距离值与边 uv 的权重之和小于 v 的距离值，则更新 v 的距离值。

使用Prims算法对Dijkstra算法的复杂度分析：

时间复杂度： O(V2)
辅助空间： O(V)

3. Dijkstra 边数最少的最短路径

在此实现中，我们给出了一个邻接矩阵图，表示给定图中节点之间的路径。任务是找到具有最少边数的最短路径，即如果存在多条具有相同成本的短路径，则选择边数最少的一条。

考虑下面给出的图表：

例子

从顶点0 到顶点 3 有两条路径，权重为 12：

0 -> 1 -> 2 -> 3
0 -> 4 -> 3

由于 Dijkstra 算法是一种贪心算法，每次迭代都会寻找最小加权顶点，因此原始 Dijkstra 算法将输出第一条路径，但结果应该是第二条路径，因为它包含最少数量的边。

例子：

输入：graph[][] = { {0, 1, INFINITY, INFINITY, 10},
{1, 0, 4, INFINITY, INFINITY},
{INFINITY, 4, 0, 7, INFINITY},
{INFINITY, INFINITY, 7, 0, 2},
{10, 无穷大, 无穷大, 2, 0} };
输出：0->4->3
INFINITY 这里表明 u 和 v 不是邻居

输入：graph[][] = { {0, 5, INFINITY, INFINITY},
{5, 0, 5, 10},
{INFINITY, 5, 0, 5},
{INFINITY, 10, 5, 0} };
输出：0->1- >3

方法： 该算法的思想是使用原始的 Dijkstra 算法，同时还通过一个数组来跟踪路径的长度，该数组存储从源顶点开始的路径长度，因此如果我们找到一条较短的路径同样的重量，那么我们就拿它。

复杂度分析：

时间复杂度 ：O(V^2)，其中 V 是顶点数，E 是边数。
辅助空间 ：O(V + E)

4. Dijkstra使用Set的最短路径算法

给定一个图和图中的源顶点，找到从源到给定图中所有顶点的最短路径

例子：

例子

输出： 0 2 6 7 17 22 19

下面是基于集合数据结构的算法。

1）将所有顶点的距离初始化为无穷大。
2）创建一个空集。集合中的每个项目都是一对（权重、顶点）。重量（或距离）用作对的第一项，因为第一项默认用于比较两对。
3) 将源顶点插入集合中，并使其距离为0。
4) 当集合不为空时，执行以下操作

a) 从 Set 中提取最小距离顶点。

令提取的顶点为u。

b) 循环遍历所有相邻的 u 并执行

对于每个顶点 v 如下。
// 如果存在通过 u 到达 v 的更短路径。

如果 dist[v] > dist[u] + Weight(u, v)
(i) 更新 v 的距离，即 dist[v] = dist[u] + Weight(u, v)

(i) 如果 v 在集合中，则通过先删除它，然后插入新距离来更新其在集合中的距离

(ii) 如果 v 不在集合中，则将其以新距离插入集合中

5) 打印距离数组 dist[ ] 以打印所有最短路径。

复杂度分析：

时间复杂度 ：O(ELogV)，其中 V 是顶点数，E 是边数。
辅助空间 ：O(V2)

Dijkstra算法的复杂度分析：

Dijkstra算法的时间复杂度取决于优先级队列所使用的数据结构。以下是基于不同实现的时间复杂度的细分：

使用未排序的列表 作为优先级队列： O(V ² ) ，其中 V 是图中的顶点数。在每次迭代中，算法都会在所有未访问的顶点中搜索距离最小的顶点，这需要 O(V) 时间。该操作执行 V 次，时间复杂度为 O(V^2)。
使用排序列表 或 二叉堆 作为优先级队列： O(E + V log V) ，其中 E 是图中的边数。在每次迭代中，算法都会提取与优先级队列距离最小的顶点，这需要 O(log V) 时间。相邻顶点的距离更新总共需要 O(E) 时间。该操作执行了 V 次，时间复杂度为 O(V log V + E log V)。由于E最多可以是V^2，所以时间复杂度为O(E + V log V)。

Dijkstra 算法与 Bellman-Ford 算法

Dijkstra 算法和 Bellman-Ford 算法都用于查找加权图中的最短路径，但它们有一些关键的区别。以下是 Dijkstra 算法和 Bellman-Ford 算法的主要区别：

特征：	迪克斯特拉氏	贝尔曼·福特
优化	针对查找具有非负边权重的图中单个源节点和所有其他节点之间的最短路径进行了优化	Bellman-Ford 算法经过优化，用于查找具有负边权重的图中单个源节点与所有其他节点之间的最短路径。
松弛	Dijkstra 算法使用贪心方法，选择距离最小的节点并更新其邻居	Bellman-Ford 算法在每次迭代中放松所有边，通过考虑到该节点的所有可能路径来更新每个节点的距离
时间复杂度	Dijkstra 算法的时间复杂度对于稠密图为 O(V^2)，对于稀疏图为 O(E log V)，其中 V 是图中的顶点数，E 是图中的边数。	Bellman-Ford 算法的时间复杂度为 O(VE)，其中 V 是图中的顶点数，E 是图中的边数。
负权重	Dijkstra 算法不适用于具有负边权重的图，因为它假设所有边权重都是非负的。	Bellman-Ford 算法可以处理负边权重，并且可以检测图中的负权重循环。

Dijkstra 算法与 Floyd-Warshall 算法

Dijkstra 算法和 Floyd-Warshall 算法都用于查找加权图中的最短路径，但它们有一些关键区别。以下是 Dijkstra 算法和 Floyd-Warshall 算法之间的主要区别：

特征：	迪克斯特拉氏	弗洛伊德-沃歇尔算法
优化	针对在具有非负边权重的图中查找单个源节点和所有其他节点之间的最短路径进行了优化	Floyd-Warshall 算法针对查找图中所有节点对之间的最短路径进行了优化。
技术	Dijkstra算法是一种单源最短路径算法，它使用贪心方法，计算从源节点到图中所有其他节点的最短路径。	另一方面，Floyd-Warshall 算法是一种全对最短路径算法，它使用动态规划来计算图中所有节点对之间的最短路径。
时间复杂度	Dijkstra 算法的时间复杂度对于稠密图为 O(V^2)，对于稀疏图为 O(E log V)，其中 V 是图中的顶点数，E 是图中的边数。	另一方面，Floyd-Warshall 算法是一种全对最短路径算法，它使用动态规划来计算图中所有节点对之间的最短路径。
负权重	Dijkstra 算法不适用于具有负边权重的图，因为它假设所有边权重都是非负的。	另一方面，Floyd-Warshall 算法是一种全对最短路径算法，它使用动态规划来计算图中所有节点对之间的最短路径。

Dijkstra 算法与 A* 算法

Dijkstra 算法和 A* 算法都用于查找加权图中的最短路径，但它们有一些关键区别。以下是Dijkstra算法与A*算法的主要区别：

特征：		A*算法
搜索技巧	针对在具有非负边权重的图中查找单个源节点和所有其他节点之间的最短路径进行了优化	A*算法是一种知情搜索算法，它使用启发式函数引导搜索向目标节点前进。
启发式函数	Dijkstra 算法不使用任何启发式函数并考虑图中的所有节点。	A*算法使用启发式函数来估计从当前节点到目标节点的距离。这种启发式函数是可接受的，这意味着它永远不会高估到目标节点的实际距离
时间复杂度	Dijkstra 算法的时间复杂度对于稠密图为 O(V^2)，对于稀疏图为 O(E log V)，其中 V 是图中的顶点数，E 是图中的边数。	A*算法的时间复杂度取决于启发式函数的质量。
应用	Dijkstra 算法用于许多应用，例如路由算法、GPS 导航系统和网络分析	。 A* 算法常用于寻路和图遍历问题，例如视频游戏、机器人和规划算法。

Dijkstra 算法练习题：

Dijkstra的最短路径算法| 贪心算法7
Dijkstra 邻接表表示算法 | 贪心算法 8
Dijkstra 算法 – 优先级队列和数组实现
Dijkstra在STL中使用set的最短路径算法
Dijkstra的最短路径算法在C++中使用STL
使用STL的priority_queue的Dijkstra最短路径算法
Dijkstra 在 C++ 中使用矩阵的最短路径算法
DAG 中单源最短路径的 Dijkstra 算法
使用斐波那契堆的 Dijkstra 算法
Dijkstra 负权有向图的最短路径算法
在 Dijkstra 的最短路径算法中打印路径
双向 Dijkstra 算法
Java中带优先级队列的Dijkstra最短路径算法
Java中Dijkstra的邻接表最短路径算法
Java中使用邻接矩阵的Dijkstra最短路径算法
在 Python 中使用邻接表的 Dijkstra 算法
Dijkstra 算法在 Python 中使用 PriorityQueue
Dijkstra 算法在 Python 中使用 heapq 模块
在Python中使用字典和优先级队列的Dijkstra算法

结论： 总体而言，Dijkstra 算法是一种在具有非负边权的图中查找最短路径的简单而有效的方法。但是，它可能不适用于具有负边权重或循环的图。在这种情况下，可以使用更先进的算法，例如贝尔曼-福特算法或弗洛伊德-沃歇尔算法。

Dijkstra(迪杰斯特拉)算法 可视化交互式动画版

什么是 Dijkstra 算法？

需要 Dijkstra 算法（目的和用例）

Dijkstra算法的基本特征

实施 Dijkstra 算法的基本要求

Dijkstra 算法可以同时适用于有向图和无向图吗？

Dijkstra 算法的算法 ：

Dijkstra 算法是如何工作的？

Dijkstra 算法的伪代码

实施 Dijkstra 算法的方法：

1. 使用priority_queue（堆）的Dijkstra最短路径算法

C++

Java

Python3

C#

Javascript

2. 使用Prim算法的Dijkstra最短路径算法

3. Dijkstra 边数最少的最短路径

4. Dijkstra使用Set的最短路径算法

Dijkstra算法的复杂度分析：

Dijkstra 算法与 Bellman-Ford 算法

Dijkstra 算法与 Floyd-Warshall 算法

Dijkstra 算法与 A* 算法

Dijkstra 算法练习题：

Dijkstra(迪杰斯特拉)算法可视化交互式动画版

Dijkstra 算法的算法：