折半查找可视化交互式动画版

二分搜索折半查找(Binary Search) 被定义为一种在排序数组中使用的搜索算法，通过 重复将搜索间隔一分为二 。二分查找的思想是利用数组已排序的信息，将时间复杂度降低到O(log N)。

二分查找算法示例

何时在数据结构中应用二分查找的条件：

应用二分查找算法：

数据结构必须是有序的。
访问数据结构的任何元素都需要恒定的时间。

二分查找算法：

在这个算法中，

通过查找中间索引“mid” 将搜索空间分为两半。

在二分查找算法中查找中间索引“mid”

将搜索空间的中间元素与键进行比较。

如果在中间元素找到密钥，则过程终止。

如果在中间元素没有找到键，则选择哪一半将用作下一个搜索空间。

如果键小于中间元素，则使用左侧进行下一步搜索。

如果键大于中间元素，则使用右侧进行下一步搜索。

这个过程一直持续到找到密钥或者总搜索空间耗尽为止。

二分查找如何工作？

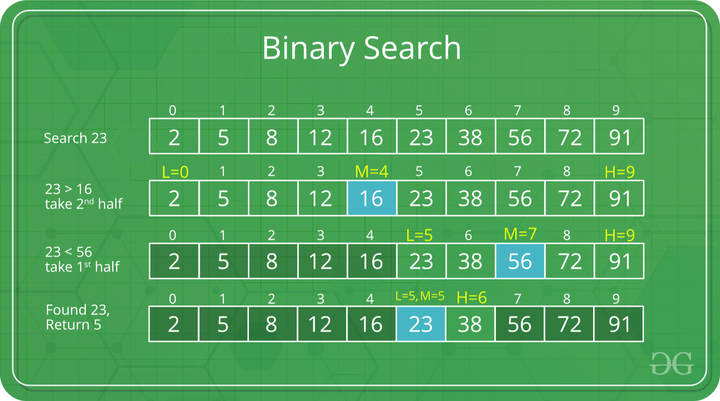
要了解二分搜索折半查找(Binary Search)的工作原理，请考虑下图：

考虑一个数组 arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91} ， 目标 = 23 。

第一步： 计算mid并将mid元素与key进行比较。如果键小于 mid 元素，则向左移动，如果大于 mid 则将搜索空间向右移动。

键（即 23）大于当前中间元素（即 16）。搜索空间向右移动。

二分查找算法：将键与 16 进行比较

密钥小于当前的中间 56。搜索空间向左移动。

二分查找算法：将键与 56 进行比较

第二步： 如果key与mid元素的值匹配，则找到该元素并停止搜索。

二分搜索折半查找(Binary Search)算法：与 mid 的关键匹配

如何实现二分查找？

二分查找算法 可以通过以下两种方式实现

迭代二分搜索折半查找(Binary Search)算法
递归二分查找算法

下面给出了这些方法的伪代码。

1.迭代二分查找算法：

这里我们使用 while 循环来继续比较键并将搜索空间分成两半的过程。

迭代二分搜索折半查找(Binary Search)算法的实现：

C++

              
                
                    // C++ program to implement iterative Binary Search
#include <bits/stdc++.h>
using namespace std;
 
// An iterative binary search function.
int binarySearch(int arr[], int l, int r, int x)
                        
{
    while (l <= r) {
        int m = l + (r - l) / 2;
 
        // Check if x is present at mid
        if (arr[m] == x)
            return m;
 
        // If x greater, ignore left half
        if (arr[m] < x)
            l = m + 1;
 
        // If x is smaller, ignore right half
        else
            r = m - 1;
    }
 
    // If we reach here, then element was not present
    return -1;
}
 
// Driver code
int main(void)
                        
{
    int
                          arr[] = { 2, 3, 4, 10, 40 };
    int
                          x = 10;
    int
                          n = sizeof(arr) / sizeof(arr[0]);
    int
                          result = binarySearch(arr, 0, n - 1, x);
    (result == -1)
        ? cout << "Element is not present in array"
        : cout << "Element is present at index " << result;
    return 0;
}

                  

              
            

C

              
                
                    // C program to implement iterative Binary Search
#include <stdio.h>
                        
 
// An iterative binary search function.
int binarySearch(int arr[], int l, int r, int x)
                        
{
    while (l <= r) {
        int m = l + (r - l) / 2;
 
        // Check if x is present at mid
        if (arr[m] == x)
            return m;
 
        // If x greater, ignore left half
        if (arr[m] < x)
            l = m + 1;
 
        // If x is smaller, ignore right half
        else
            r = m - 1;
    }
 
    // If we reach here, then element was not present
    return -1;
}
 
// Driver code
int main(void)
                        
{
    int
                          arr[] = { 2, 3, 4, 10, 40 };
    int
                          n = sizeof(arr) / sizeof(arr[0]);
    int
                          x = 10;
    int
                          result = binarySearch(arr, 0, n - 1, x);
    (result == -1) ? printf("Element is not present"
                            " in array")
                   : printf("Element is present at "
                            "index %d",
                            result);
    return 0;
}

                  

              
            

Java

              
                
                    // Java implementation of iterative Binary Search
 
import java.io.*;
 
class BinarySearch {
   
                        
    // Returns index of x if it is present in arr[].
    int
                          binarySearch(int arr[], int x)
                        
    {
        int l = 0, r = arr.length - 1;
        while (l <= r) {
            int m = l + (r - l) / 2;
 
            // Check if x is present at mid
            if (arr[m] == x)
                return m;
 
            // If x greater, ignore left half
            if (arr[m] < x)
                l = m + 1;
 
            // If x is smaller, ignore right half
            else
                r = m - 1;
        }
 
        // If we reach here, then element was
        // not present
        return -1;
    }
 
    // Driver code
    public
                          static void main(String args[])
    {
        BinarySearch ob = new BinarySearch();
        int arr[] = { 2, 3, 4, 10, 40 };
        int n = arr.length;
        int x = 10;
        int result = ob.binarySearch(arr, x);
                        
        if (result == -1)
            System.out.println(
                "Element is not present in array");
        else
            System.out.println("Element is present at "
                        
                               + "index " + result);
    }
}

                  

              
            

Python3

              
                
                    # Python3 code to implement iterative Binary
# Search.
 
 
# It returns location of x in given array arr
def binarySearch(arr, l, r, x):
 
    while
                          l <= r:
                        
 
        mid = l + (r - l) // 2
 
        # Check if x is present at mid
        if arr[mid] == x:
            return mid
 
        # If x is greater, ignore left half
        elif arr[mid] < x:
            l = mid + 1
 
        # If x is smaller, ignore right half
        else:
            r = mid - 1
 
    # If we reach here, then the element
    # was not present
    return
                          -1
 
 
# Driver Code
if __name__ ==
                          '__main__':
    arr = [2, 3, 4, 10, 40]
    x = 10
 
    # Function call
    result = binarySearch(arr, 0, len(arr)-1, x)
    if
                          result != -1:
        print("Element is present at index", result)
                        
    else:
        print("Element is not present in array")

                  

              
            

C＃

              
                
                    // C# implementation of iterative Binary Search
using System;
 
class GFG {
     
    // Returns index of x if it is present in arr[]
    static
                          int binarySearch(int[] arr, int x)
    {
        int l = 0, r = arr.Length - 1;
        while (l <= r) {
            int m = l + (r - l) / 2;
 
            // Check if x is present at mid
            if (arr[m] == x)
                return m;
 
            // If x greater, ignore left half
            if (arr[m] < x)
                l = m + 1;
 
            // If x is smaller, ignore right half
            else
                r = m - 1;
        }
 
        // If we reach here, then element was
        // not present
        return -1;
    }
 
    // Driver code
    public
                          static void Main()
    {
        int[] arr = { 2, 3, 4, 10, 40 };
        int n = arr.Length;
        int x = 10;
        int result = binarySearch(arr, x);
        if (result == -1)
            Console.WriteLine(
                "Element is not present in array");
        else
            Console.WriteLine("Element is present at "
                        
                              + "index " + result);
    }
}

                  

              
            

JavaScript

              
                
                    // Program to implement iterative Binary Search
 
  
// A iterative binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
 
 function binarySearch(arr, x)
{    
    let l = 0;
    let r = arr.length - 1;
    let mid;
                        
    while
                          (r >= l) {
         mid = l + Math.floor((r - l) / 2);
  
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
  
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            r = mid - 1;
             
                        
        // Else the element can only be present
        // in right subarray
        else
            l = mid + 1;
    }
  
    // We reach here when element is not
    // present in array
    return
                          -1;
}
 
    arr =new Array(2, 3, 4, 10, 40);
    x = 10;
                        
    n = arr.length;
    result = binarySearch(arr, x);
     
(result == -1) ? console.log("Element is not present in array")
               : console.log ("Element is present at index " + result);
                        
                
                        
// This code is contributed by simranarora5sos and rshuklabbb

                  

              
            

PHP

              
                
                    <?php
// PHP program to implement
                        
// iterative Binary Search
                        
 
// An iterative binary search 
// function
function binarySearch($arr, $l, 
                      $r, $x)
{
    while
                          ($l <= $r)
                        
    {
        $m = $l
                          + ($r - $l) / 2;
                        
 
        // Check if x is present at mid
        if ($arr[$m] == $x)
            return floor($m);
 
        // If x greater, ignore
        // left half
        if ($arr[$m] < $x)
            $l = $m
                          + 1;
 
        // If x is smaller, 
        // ignore right half
        else
            $r = $m
                          - 1;
    }
 
    // If we reach here, then 
    // element was not present
    return
                          -1;
}
 
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$n = count($arr);
$x = 10;
$result = binarySearch($arr, 0, 
                       $n - 1, $x);
if(($result == -1))
echo "Element is not present in array";
else
echo "Element is present at index ", 
                            $result;
 
// This code is contributed by anuj_67.
?>

                  

              
            

输出

元素出现在索引 3 处

时间复杂度： O(log N)
辅助空间： O(1)

2.递归二分查找算法：

创建一个递归函数并将搜索空间的中间部分与键进行比较。并根据结果返回找到键的索引或调用下一个搜索空间的递归函数。

递归二分查找算法的实现：

C++

              
                
                    // C++ program to implement recursive Binary Search
#include <bits/stdc++.h>
using namespace std;
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
                        
{
    if
                          (r >= l) {
        int mid = l + (r - l) / 2;
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
 
    // We reach here when element is not
    // present in array
    return -1;
}
 
// Driver code
int main()
{
    int
                          arr[] = { 2, 3, 4, 10, 40 };
    int
                          x = 10;
    int
                          n = sizeof(arr) / sizeof(arr[0]);
    int
                          result = binarySearch(arr, 0, n - 1, x);
    (result == -1)
        ? cout << "Element is not present in array"
        : cout << "Element is present at index " << result;
    return 0;
}

                  

              
            

C

              
                
                    // C program to implement recursive Binary Search
#include <stdio.h>
                        
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
                        
{
    if
                          (r >= l) {
        int mid = l + (r - l) / 2;
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
 
    // We reach here when element is not
    // present in array
    return -1;
}
 
// Driver code
int main()
{
    int
                          arr[] = { 2, 3, 4, 10, 40 };
    int
                          n = sizeof(arr) / sizeof(arr[0]);
    int
                          x = 10;
    int
                          result = binarySearch(arr, 0, n - 1, x);
    (result == -1)
        ? printf("Element is not present in array")
        : printf("Element is present at index %d", result);
    return 0;
}

                  

              
            

Java

              
                
                    // Java implementation of recursive Binary Search
class BinarySearch {
 
    // Returns index of x if it is present in arr[l..
    // r], else return -1
    int
                          binarySearch(int arr[], int l, int r, int x)
    {
        if (r >= l) {
            int mid = l + (r - l) / 2;
 
            // If the element is present at the
            // middle itself
            if (arr[mid] == x)
                return mid;
 
            // If element is smaller than mid, then
            // it can only be present in left subarray
            if (arr[mid] > x)
                return binarySearch(arr, l, mid - 1, x);
 
            // Else the element can only be present
            // in right subarray
            return binarySearch(arr, mid + 1, r, x);
        }
 
        // We reach here when element is not present
        // in array
        return -1;
    }
 
    // Driver code
    public
                          static void main(String args[])
    {
        BinarySearch ob = new BinarySearch();
        int arr[] = { 2, 3, 4, 10, 40 };
        int n = arr.length;
        int x = 10;
        int result = ob.binarySearch(arr, 0, n - 1, x);
        if (result == -1)
            System.out.println(
                "Element is not present in array");
        else
            System.out.println(
                "Element is present at index " + result);
                        
    }
}
/* This code is contributed by Rajat Mishra */

                  

              
            

Python3

              
                    # Python3 Program for recursive binary search.
 
# Returns index of x in arr if present, else -1
def binarySearch(arr, l, r, x):
 
    # Check base case
    if
                          r >= l:
                        
        mid = l + (r - l) // 2
 
        # If element is present at the middle itself
        if arr[mid] == x:
            return mid
 
        # If element is smaller than mid, then it
        # can only be present in left subarray
        elif arr[mid] > x:
            return binarySearch(arr, l, mid-1, x)
 
        # Else the element can only be present
        # in right subarray
        else:
            return binarySearch(arr, mid + 1, r, x)
                        
    # Element is not present in the array
    else:
        return -1
                        
# Driver Code
if __name__ ==
                          '__main__':
    arr = [2, 3, 4, 10, 40]
    x = 10
     
    # Function call
    result = binarySearch(arr, 0, len(arr)-1, x)
     
    if
                          result != -1:
        print("Element is present at index", result)
                        
    else:
        print("Element is not present in array")

C＃

              
                
                    // C# implementation of recursive Binary Search
using System;
 
class GFG {
 
    // Returns index of x if it is present in
    // arr[l..r], else return -1
    static
                          int binarySearch(int[] arr, int l, int
                          r, int x)
                        
    {
        if (r >= l) {
            int mid = l + (r - l) / 2;
 
            // If the element is present at the
            // middle itself
            if (arr[mid] == x)
                return mid;
 
            // If element is smaller than mid, then
            // it can only be present in left subarray
            if (arr[mid] > x)
                return binarySearch(arr, l, mid - 1, x);
                        
 
            // Else the element can only be present
            // in right subarray
            return binarySearch(arr, mid + 1, r, x);
                        
        }
 
        // We reach here when element is not present
        // in array
        return -1;
    }
 
    // Driver code
    public
                          static void Main()
    {
 
        int[] arr = { 2, 3, 4, 10, 40 };
        int n = arr.Length;
        int x = 10;
 
        int result = binarySearch(arr, 0, n - 1, x);
 
        if (result == -1)
            Console.WriteLine(
                "Element is not present in arrau");
        else
            Console.WriteLine("Element is present at index "
                              + result);
    }
}
 
// This code is contributed by Sam007.

                  

              
            

JavaScript

              
                
                    // JavaScript program to implement recursive Binary Search
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
function binarySearch(arr, l, r, x){
    if
                          (r >= l) {
        let mid = l + Math.floor((r - l) / 2);
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
                        
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
                        
    }
 
    // We reach here when element is not
    // present in array
    return
                          -1;
}
 
let arr = [ 2, 3, 4, 10, 40 ];
let x = 10;
let n = arr.length
let result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? console.log( "Element is not present in array")
               : console.log("Element is present at index " +result);
                        

                  

              
            

PHP

              
                
                    <?php
// PHP program to implement
                        
// recursive Binary Search
                        
 
// A recursive binary search
                        
// function. It returns location
// of x in given array arr[l..r] 
// is present, otherwise -1
                        
function binarySearch($arr, $l, $r, $x)
{
if ($r >= $l)
                        
{
        $mid = ceil($l
                          + ($r - $l) / 2);
                        
 
        // If the element is present 
        // at the middle itself
        if ($arr[$mid] == $x) 
            return floor($mid);
 
        // If element is smaller than 
        // mid, then it can only be 
        // present in left subarray
        if ($arr[$mid] > $x) 
            return binarySearch($arr, $l, 
                                $mid - 1, $x);
 
        // Else the element can only 
        // be present in right subarray
        return binarySearch($arr, $mid
                          + 1, 
                            $r, $x);
}
 
// We reach here when element 
// is not present in array
                        
return -1;
}
 
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$n = count($arr);
$x = 10;
$result = binarySearch($arr, 0, $n - 1, $x);
                        
if(($result == -1))
echo "Element is not present in array";
else
echo "Element is present at index ",
                            $result;
                             
                        
// This code is contributed by anuj_67.
?>

                  

              
            

输出

元素出现在索引 3 处

二分查找的复杂度分析：

时间复杂度：
- 最佳情况：O(1)
- 平均情况：O(log N)
- 最坏情况：O(log N)
辅助空间： O(1)，如果考虑递归调用栈则辅助空间为O(logN)。

二分查找的优点：

二分查找比线性查找更快，特别是对于大型数组。
比具有类似时间复杂度的其他搜索算法（例如插值搜索或指数搜索）更有效。
二分搜索折半查找(Binary Search)非常适合搜索存储在外部存储器（例如硬盘驱动器或云中）中的大型数据集。

二分查找的缺点：

数组应该是排序的。
二分查找要求将要查找的数据结构存储在连续的内存位置中。
二分查找要求数组的元素是可比较的，这意味着它们必须能够排序。

二分查找的应用：

二分搜索折半查找(Binary Search)可以用作机器学习中使用的更复杂算法的构建块，例如训练神经网络或查找模型的最佳超参数的算法。
它可用于计算机图形学中的搜索，例如光线追踪或纹理映射的算法。
它可用于搜索数据库。

折半查找 可视化交互式动画版

何时在数据结构中应用二分查找的条件：

二分查找算法：

二分查找如何工作？

如何实现二分查找？

1.迭代二分查找算法：

C++

C

Java

Python3

C＃

JavaScript

PHP

2.递归二分查找算法：

C++

C

Java

Python3

C＃

JavaScript

PHP

二分查找的复杂度分析：

二分查找的优点：

二分查找的缺点：

二分查找的应用：

折半查找可视化交互式动画版