堆排序可视化交互式动画版

堆排序是一种基于 二叉堆数据结构的比较排序技术。它类似于选择排序，我们首先找到最小元素并将最小元素放在开头。对其余元素重复相同的过程。

堆排序算法

要解决该问题，请遵循以下想法：

首先使用heapify将数组转换为堆数据结构，然后逐个删除Max-heap的根节点并替换为堆中的最后一个节点，然后对堆的根进行heapify。重复此过程，直到堆的大小大于 1。

从给定的输入数组构建一个堆。

重复以下步骤，直到堆只包含一个元素：

将堆的根元素（最大的元素）与堆的最后一个元素交换。

删除堆的最后一个元素（现在位于正确的位置）。

堆化堆的剩余元素。

排序数组是通过反转输入数组中元素的顺序获得的。

堆排序的详细工作原理

为了更清楚地理解堆排序，让我们采用一个未排序的数组并尝试使用堆排序对其进行排序。
考虑数组：arr[] = {4, 10, 3, 5, 1}。

构建完整二叉树： 从数组构建完整二叉树。

堆排序算法| 构建完全二叉树

转换为最大堆： 之后，任务是从未排序的数组构造一棵树，并尝试将其转换为最大堆。

要将堆转换为最大堆，父节点应始终大于或等于子节点

在此示例中，由于父节点 4 小于子节点 10， 因此将它们交换以构建最大堆。

现在，作为父级的 4 小于子级 5 ，因此再次交换这两个值，结果堆和数组应如下所示：

堆排序算法| Max Heapify构造二叉树

执行堆排序： 删除每一步中的最大元素（即，将其移动到结束位置并将其删除），然后考虑剩余元素并将其转换为最大堆。

从最大堆中删除根元素 (10) 。 为了删除这个节点，尝试将它与最后一个节点交换，即 (1)。 删除根元素后，再次对其进行堆化，将其转换为最大堆。

结果堆和数组应如下所示：

堆排序算法| 从 root 和 max heapify 中删除最大值

重复上面的步骤，就会像下面这样：

堆排序算法| 从根和最大堆中删除下一个最大值

现在再次删除根（即3）并执行heapify。

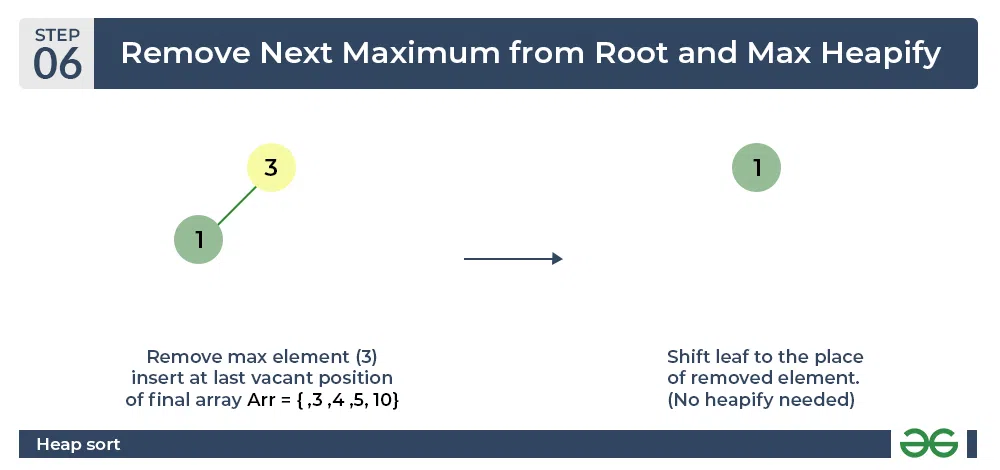
堆排序算法| 重复上一步

现在，当根再次被删除时，它就被排序了。排序后的数组将类似于 arr[] = {1, 3, 4, 5, 10} 。

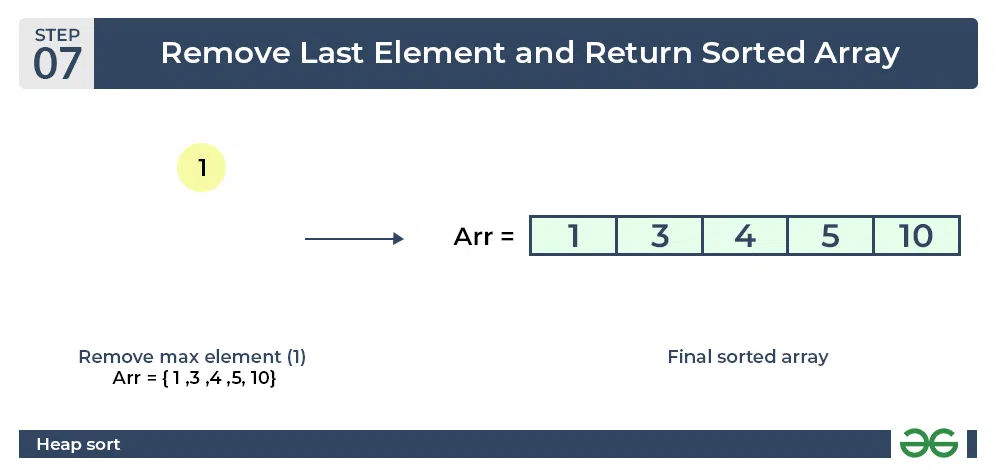
堆排序算法| 最终排序数组

堆排序的实现

C++

              
                
                    // C++ program for implementation of Heap Sort
 
#include <iostream>
using namespace std;
 
// To heapify a subtree rooted with node i
// which is an index in arr[].
// n is size of heap
void heapify(int arr[], int N, int i)
                        
{
 
    // Initialize largest as root
    int
                          largest = i;
 
    // left = 2*i + 1
    int
                          l = 2 * i + 1;
 
    // right = 2*i + 2
    int
                          r = 2 * i + 2;
 
    // If left child is larger than root
    if
                          (l < N && arr[l] > arr[largest])
        largest = l;
 
    // If right child is larger than largest
    // so far
    if
                          (r < N && arr[r] > arr[largest])
        largest = r;
 
    // If largest is not root
    if
                          (largest != i) {
        swap(arr[i], arr[largest]);
 
        // Recursively heapify the affected
        // sub-tree
        heapify(arr, N, largest);
    }
}
 
// Main function to do heap sort
void heapSort(int arr[], int N)
{
 
    // Build heap (rearrange array)
    for (int i = N / 2 - 1; i >= 0; i--)
                        
        heapify(arr, N, i);
 
    // One by one extract an element
    // from heap
    for (int i = N - 1; i > 0; i--) {
 
        // Move current root to end
        swap(arr[0], arr[i]);
 
        // call max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}
 
// A utility function to print array of size n
void printArray(int arr[], int N)
{
    for (int i = 0; i < N; ++i)
        cout << arr[i] << " ";
    cout << "\n";
}
 
// Driver's code
int main()
{
    int
                          arr[] = { 12, 11, 13, 5, 6, 7 };
    int
                          N = sizeof(arr) / sizeof(arr[0]);
 
    // Function call
    heapSort(arr, N);
 
    cout << "Sorted array is \n";
    printArray(arr, N);
}

                  

              
            

C

              
                
                    // Heap Sort in C
 
#include <stdio.h>
                        
 
// Function to swap the position of two elements
 
void swap(int* a, int* b)
{
 
    int
                          temp = *a;
    *a = *b;
                        
    *b = temp;
}
 
// To heapify a subtree rooted with node i
// which is an index in arr[].
// n is size of heap
void heapify(int arr[], int N, int i)
                        
{
    // Find largest among root,
    // left child and right child
 
    // Initialize largest as root
    int
                          largest = i;
 
    // left = 2*i + 1
    int
                          left = 2 * i + 1;
 
    // right = 2*i + 2
    int
                          right = 2 * i + 2;
 
    // If left child is larger than root
    if
                          (left < N && arr[left] > arr[largest])
 
        largest = left;
 
    // If right child is larger than largest
    // so far
    if
                          (right < N && arr[right] > arr[largest])
 
        largest = right;
 
    // Swap and continue heapifying
    // if root is not largest
    // If largest is not root
    if
                          (largest != i) {
 
        swap(&arr[i], &arr[largest]);
 
        // Recursively heapify the affected
        // sub-tree
        heapify(arr, N, largest);
    }
}
 
// Main function to do heap sort
void heapSort(int arr[], int N)
{
 
    // Build max heap
    for (int i = N / 2 - 1; i >= 0; i--)
                        
 
        heapify(arr, N, i);
 
    // Heap sort
    for (int i = N - 1; i >= 0; i--) {
 
        swap(&arr[0], &arr[i]);
 
        // Heapify root element
        // to get highest element at
        // root again
        heapify(arr, i, 0);
    }
}
 
// A utility function to print array of size n
void printArray(int arr[], int N)
{
    for (int i = 0; i < N; i++)
        printf("%d ", arr[i]);
    printf("\n");
}
 
// Driver's code
int main()
{
    int
                          arr[] = { 12, 11, 13, 5, 6, 7 };
    int
                          N = sizeof(arr) / sizeof(arr[0]);
 
    // Function call
    heapSort(arr, N);
    printf("Sorted array is\n");
    printArray(arr, N);
}
 
// This code is contributed by _i_plus_plus_.

                  

              
            

Java

              
                
                    // Java program for implementation of Heap Sort
 
public class HeapSort {
    public
                          void sort(int arr[])
    {
        int N = arr.length;
 
        // Build heap (rearrange array)
        for (int
                          i = N / 2 - 1; i >= 0; i--)
                        
            heapify(arr, N, i);
 
        // One by one extract an element from heap
        for (int
                          i = N - 1; i > 0; i--) {
            // Move current root to end
            int temp = arr[0];
            arr[0] = arr[i];
                        
            arr[i] = temp;
 
            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
 
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    void
                          heapify(int arr[], int N, int i)
    {
        int largest = i; // Initialize largest as root
        int l = 2 * i + 1; // left = 2*i + 1
        int r = 2 * i + 2; // right = 2*i + 2
 
        // If left child is larger than root
        if (l < N && arr[l] > arr[largest])
            largest = l;
 
        // If right child is larger than largest so far
        if (r < N && arr[r] > arr[largest])
            largest = r;
 
        // If largest is not root
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
 
            // Recursively heapify the affected sub-tree
            heapify(arr, N, largest);
        }
    }
 
    /* A utility function to print array of size n */
    static
                          void printArray(int arr[])
    {
        int N = arr.length;
 
        for (int
                          i = 0; i < N; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver's code
    public
                          static void main(String args[])
    {
        int arr[] = { 12, 11, 13, 5, 6, 7 };
        int N = arr.length;
 
        // Function call
        HeapSort ob = new HeapSort();
        ob.sort(arr);
 
        System.out.println("Sorted array is");
        printArray(arr);
    }
}

                  

              
            

Python3

              
                
                    # Python program for implementation of heap Sort
 
# To heapify subtree rooted at index i.
# n is size of heap
 
 
def heapify(arr, N, i):
    largest = i  # Initialize largest as root
                        
    l = 2 * i + 1     # left = 2*i + 1
    r = 2 * i + 2     # right = 2*i + 2
 
    # See if left child of root exists and is
    # greater than root
    if
                          l < N and arr[largest] < arr[l]:
        largest = l
                        
 
    # See if right child of root exists and is
    # greater than root
    if
                          r < N and arr[largest] < arr[r]:
        largest = r
                        
 
    # Change root, if needed
    if
                          largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # swap
 
        # Heapify the root.
        heapify(arr, N, largest)
 
# The main function to sort an array of given size
 
 
def heapSort(arr):
    N = len(arr)
                        
 
    # Build a maxheap.
    for
                          i in range(N//2 - 1, -1, -1):
        heapify(arr, N, i)
 
    # One by one extract elements
    for
                          i in range(N-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # swap
        heapify(arr, i, 0)
 
 
# Driver's code
if __name__ ==
                          '__main__':
    arr = [12, 11, 13, 5, 6, 7]
 
    # Function call
    heapSort(arr)
    N = len(arr)
                        
 
    print("Sorted array is")
    for
                          i in range(N):
        print("%d"
                          % arr[i], end=" ")
# This code is contributed by Mohit Kumra

                  

              
            

C＃

              
                
                    // C# program for implementation of Heap Sort
using System;
 
public class HeapSort {
    public
                          void sort(int[] arr)
    {
        int N = arr.Length;
 
        // Build heap (rearrange array)
        for (int
                          i = N / 2 - 1; i >= 0; i--)
            heapify(arr, N, i);
 
        // One by one extract an element from heap
        for (int
                          i = N - 1; i > 0; i--) {
            // Move current root to end
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
 
            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
 
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    void
                          heapify(int[] arr, int N, int i)
    {
        int largest = i; // Initialize largest as root
        int l = 2 * i + 1; // left = 2*i + 1
        int r = 2 * i + 2; // right = 2*i + 2
 
        // If left child is larger than root
        if (l < N && arr[l] > arr[largest])
            largest = l;
 
        // If right child is larger than largest so far
        if (r < N && arr[r] > arr[largest])
            largest = r;
 
        // If largest is not root
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
 
            // Recursively heapify the affected sub-tree
            heapify(arr, N, largest);
        }
    }
 
    /* A utility function to print array of size n */
    static
                          void printArray(int[] arr)
    {
        int N = arr.Length;
        for (int
                          i = 0; i < N; ++i)
            Console.Write(arr[i] + " ");
        Console.Read();
    }
 
    // Driver's code
    public
                          static void Main()
    {
        int[] arr = { 12, 11, 13, 5, 6, 7 };
        int N = arr.Length;
 
        // Function call
        HeapSort ob = new HeapSort();
        ob.sort(arr);
 
        Console.WriteLine("Sorted array is");
        printArray(arr);
    }
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

                  

              
            

JavaScript

              
                
                    // JavaScript program for implementation
// of Heap Sort
 
    function sort( arr)
    {
        var N = arr.length;
 
        // Build heap (rearrange array)
        for (var
                          i = Math.floor(N / 2) - 1; i >= 0; i--)
            heapify(arr, N, i);
 
        // One by one extract an element from heap
        for (var
                          i = N - 1; i > 0; i--) {
            // Move current root to end
            var temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
 
            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
 
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    function heapify(arr, N, i)
    {
        var largest = i; // Initialize largest as root
        var l = 2 * i + 1; // left = 2*i + 1
        var r = 2 * i + 2; // right = 2*i + 2
 
        // If left child is larger than root
        if (l < N && arr[l] > arr[largest])
            largest = l;
 
        // If right child is larger than largest so far
        if (r < N && arr[r] > arr[largest])
            largest = r;
 
        // If largest is not root
        if (largest != i) {
            var swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
 
            // Recursively heapify the affected sub-tree
            heapify(arr, N, largest);
        }
    }
 
    /* A utility function to print array of size n */
    function printArray(arr)
    {
        var N = arr.length;
        for (var
                          i = 0; i < N; ++i)
            document.write(arr[i] + " ");
         
    }
 
 
    var
                          arr = [12, 11, 13, 5, 6, 7];
    var
                          N = arr.length;
 
    sort(arr);
 
    document.write( "Sorted array is");
    printArray(arr, N);
 
 
// This code is contributed by SoumikMondal

                  

              
            

PHP

              
                
                    <?php
 
// Php program for implementation of Heap Sort
 
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
function heapify(&$arr, $N, $i)
{
    $largest = $i; // Initialize largest as root
    $l
                          = 2*$i + 1; // left = 2*i + 1
    $r
                          = 2*$i + 2; // right = 2*i + 2
 
    // If left child is larger than root
    if
                          ($l < $N && $arr[$l] > $arr[$largest])
                        
        $largest = $l;
 
    // If right child is larger than largest so far
    if
                          ($r < $N && $arr[$r] > $arr[$largest])
                        
        $largest = $r;
 
    // If largest is not root
    if
                          ($largest != $i)
    {
        $swap = $arr[$i];
        $arr[$i] = $arr[$largest];
        $arr[$largest] = $swap;
 
        // Recursively heapify the affected sub-tree
        heapify($arr, $N, $largest);
    }
}
 
// main function to do heap sort
function heapSort(&$arr, $N)
{
    // Build heap (rearrange array)
    for
                          ($i = $N / 2 - 1; $i >= 0; $i--)
                        
        heapify($arr, $N, $i);
 
    // One by one extract an element from heap
    for
                          ($i = $N-1; $i > 0; $i--)
    {
        // Move current root to end
        $temp = $arr[0];
            $arr[0] = $arr[$i];
            $arr[$i] = $temp;
 
        // call max heapify on the reduced heap
        heapify($arr, $i, 0);
                        
    }
}
 
/* A utility function to print array of size n */
function printArray(&$arr, $N)
{
    for
                          ($i = 0; $i < $N; ++$i)
        echo ($arr[$i]." ") ; 
         
} 
 
    // Driver's program
    $arr
                          = array(12, 11, 13, 5, 6, 7);
    $N
                          = sizeof($arr)/sizeof($arr[0]);
     
    // Function call
    heapSort($arr, $N);
 
    echo
                          'Sorted array is ' . "\n";
     
    printArray($arr , $N);
 
// This code is contributed by Shivi_Aggarwal
?>

                  

              
            

输出

排序后的数组是
5 6 7 11 12 13

堆排序的复杂度分析

时间复杂度： O(N log N)
辅助空间： O(log n)，由于递归调用堆栈。然而，对于迭代实现来说，辅助空间可以是O(1)。

关于堆排序的要点：

堆排序是一种就地算法。
它的典型实现不稳定，但可以使其稳定（请参阅此）
通常比实现良好的 QuickSort 慢 2-3 倍。缓慢的原因是缺乏参考位置。

堆排序的优点：

高效的时间复杂度： 在所有情况下，堆排序的时间复杂度均为 O(n log n)。这使得对大型数据集进行排序变得高效。 log n 因子来自二叉堆的高度，它确保算法即使在元素数量较多的情况下也能保持良好的性能。
内存使用 – 内存使用量可以最小化，因为除了保存要排序的初始项目列表所需的内存之外，它不需要额外的内存空间来工作
简单性—— 它比其他同样高效的排序算法更容易理解，因为它不使用递归等先进的计算机科学概念。

堆排序的缺点：

成本高昂 ：堆排序的成本很高。
不稳定 ：堆排序不稳定。它可能会重新排列相对顺序。
高效： 在处理高度复杂的数据时，堆排序不是很高效。

与堆排序相关的常见问题

Q1. 堆排序分为哪两个阶段？

堆排序算法由两个阶段组成。在第一阶段，数组被转换为最大堆。在第二阶段，最高的元素（即树根处的元素）被删除，剩余的元素用于创建新的最大堆。

Q2。为什么堆排序不稳定？

堆排序算法不是一个稳定的算法。此算法不稳定，因为在堆中执行的操作可能会更改等效键的相对顺序。

Q3。堆排序是“分而治之”算法的一个例子吗？

堆排序根本不是分而治之的算法。它使用堆数据结构来有效地对其元素进行排序，而不是使用“分而治之的方法”来对元素进行排序。

Q4。哪种排序算法更好——堆排序还是归并排序？

答案在于它们的时间复杂度和空间要求的比较。归并排序比堆排序稍快。但另一方面，合并排序需要额外的内存。根据要求，应选择使用哪一种。

Q5. 为什么堆排序比选择排序更好？

堆排序与选择排序类似，但有更好的方法来获取最大元素。它利用堆数据结构在常数时间内获取最大元素