拓扑排序-栈可视化交互式动画版

有向无环图 (DAG) 的拓扑排序是顶点的线性排序，使得对于每个有向边 uv，顶点 u 在排序中位于 v之前。

注意： 如果图不是 DAG ，则无法对图进行拓扑排序。

例子：

输入： 图表：

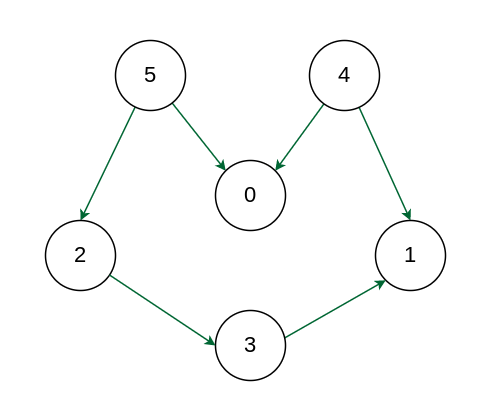
例子

输出： 5 4 2 3 1 0
解释： 拓扑排序中的第一个顶点始终是入度为 0 的顶点（没有入边的顶点）。下图的拓扑排序为“5 4 2 3 1 0”。一张图可以有不止一种拓扑排序。下图的另一种拓扑排序是“4 5 2 3 1 0”。

拓扑排序与深度优先遍历（DFS）：

在 DFS 中，我们打印一个顶点，然后递归地调用 DFS 来获取它的相邻顶点。在拓扑排序中，我们需要在其相邻顶点之前打印一个顶点。

例如， 在上面给出的图中，顶点“5”应该在顶点“0”之前打印，但与 DFS 不同的是，顶点“4”也应该在顶点“0”之前打印。所以拓扑排序与DFS不同。例如，所示图的DFS是“5 2 3 1 0 4”，但这不是拓扑排序。

拓扑排序算法：

先决条件 ： DFS

我们可以修改 DFS 来找到图的拓扑排序。在深度优先搜索中，

我们从一个顶点开始，首先打印它，然后
对其相邻顶点递归调用DFS。

在拓扑排序中：

我们使用临时堆栈。
我们不会立即打印顶点，
我们首先对其所有相邻顶点递归调用拓扑排序，然后将其压入堆栈。
最后，打印堆栈的内容。

注意： 只有当顶点的所有相邻顶点（及其相邻顶点等）都已在堆栈中时，才会将顶点压入堆栈

方法：

创建一个堆栈来存储节点。
初始化大小为 N的访问数组来保存访问节点的记录。
运行从0 到N 的循环：
如果访问 数组中的节点未标记为 True ，则调用递归函数进行拓扑排序并执行以下步骤：
- 在访问数组中将当前节点标记为 True 。
- 在与当前节点有向边的所有节点上运行循环
- 如果该节点在访问数组中未标记为 True ：
  - 在节点上递归调用拓扑排序函数
- 将当前节点压入堆栈。
打印堆栈中的所有元素。

图示拓扑排序算法：

下图是上述方法的说明：

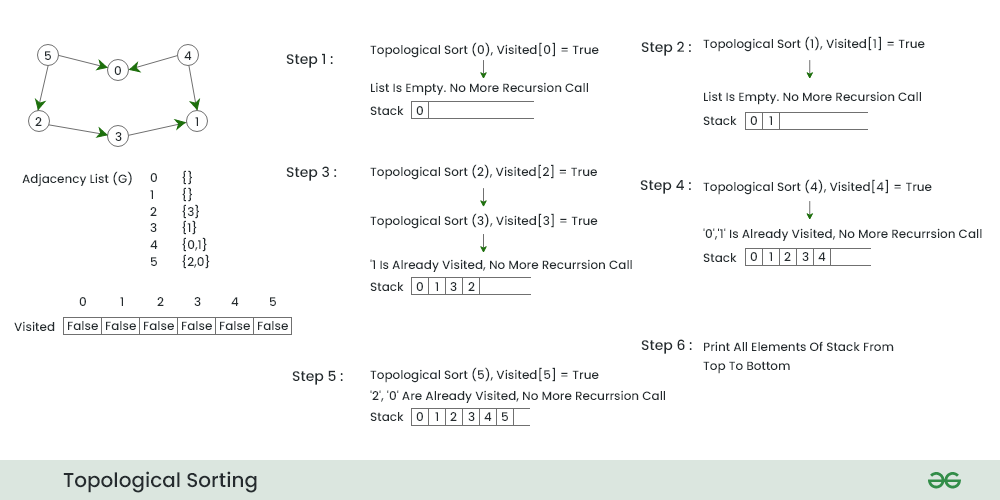
拓扑排序总体流程

步骤1：

我们从节点 0 开始 DFS，因为它有零个传入节点

我们将节点 0 压入堆栈并移动到具有最小数量相邻节点的下一个节点，即节点 1。

第2步：

在这一步中，由于该节点没有相邻节点，因此将节点1压入堆栈并移动到下一个节点。

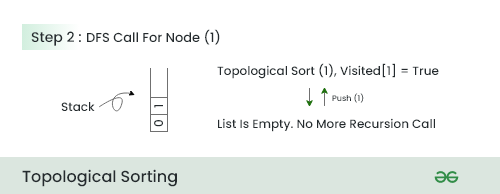
步骤3：

在这一步中，我们选择节点2，因为它在0和1之后的相邻节点数最少。

我们将节点 2 称为 DFS，并将从节点 2 开始遍历的所有节点按相反顺序压入。

所以先推 3 然后推 2 。

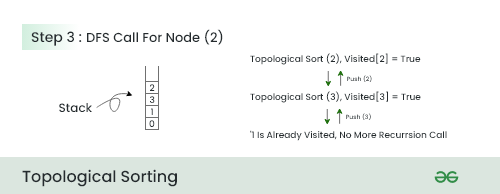
步骤4：

我们现在将节点 4 称为 DFS

因为 0 和 1 已经存在于堆栈中，所以我们只需将节点 4 压入堆栈并返回。

第5步：

在这一步中，因为 5 的所有相邻节点都已经在堆栈中，所以我们将节点 5 压入堆栈并返回。

步骤6： 这是拓扑排序的最后一步，我们从堆栈中弹出所有元素并按顺序打印它。

下面是上述方法的实现：

C++
Java
Python3
JavaScript

C++

              
                
                    // A C++ program to print topological
// sorting of a DAG
#include <bits/stdc++.h>
using namespace std;
 
// Class to represent a graph
class Graph {
    // No. of vertices'
    int
                          V;
 
    // Pointer to an array containing adjacency listsList
    list<int>* adj;
 
    // A function used by topologicalSort
    void topologicalSortUtil(int v, bool visited[],
                             stack<int>& Stack);
 
public:
    // Constructor
    Graph(int V);
 
    // function to add an edge to graph
    void addEdge(int v, int w);
 
    // prints a Topological Sort of
    // the complete graph
    void topologicalSort();
};
 
Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}
 
void Graph::addEdge(int v, int w)
                        
{
    // Add w to v’s list.
    adj[v].push_back(w);
}
 
// A recursive function used by topologicalSort
void Graph::topologicalSortUtil(int v, bool visited[],
                                stack<int>& Stack)
{
    // Mark the current node as visited.
    visited[v] = true;
 
    // Recur for all the vertices
    // adjacent to this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            topologicalSortUtil(*i, visited, Stack);
 
    // Push current vertex to stack
    // which stores result
    Stack.push(v);
}
 
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void Graph::topologicalSort()
{
    stack<int> Stack;
 
    // Mark all the vertices as not visited
    bool* visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;
 
    // Call the recursive helper function
    // to store Topological
    // Sort starting from all
    // vertices one by one
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
            topologicalSortUtil(i, visited, Stack);
 
    // Print contents of stack
    while (Stack.empty() == false) {
        cout << Stack.top() << " ";
        Stack.pop();
    }
 
    delete[] visited;
}
 
// Driver Code
int main()
{
    // Create a graph given in the above diagram
    Graph g(6);
    g.addEdge(5, 2);
    g.addEdge(5, 0);
    g.addEdge(4, 0);
    g.addEdge(4, 1);
    g.addEdge(2, 3);
    g.addEdge(3, 1);
 
    cout << "Following is a Topological Sort of the given "
            "graph \n";
 
    // Function Call
    g.topologicalSort();
 
    return 0;
}

                  

              
            

Java

              
                
                    // A Java program to print topological
// sorting of a DAG
import java.io.*;
import java.util.*;
 
// This class represents a directed graph
// using adjacency list representation
class Graph {
    // No. of vertices
    private
                          int V;
 
    // Adjacency List as ArrayList of ArrayList's
    private
                          ArrayList<ArrayList<Integer> > adj;
 
    // Constructor
    Graph(int v)
                        
    {
        V = v;
        adj = new ArrayList<ArrayList<Integer> >(v);
        for (int
                          i = 0; i < v; ++i)
            adj.add(new ArrayList<Integer>());
    }
 
    // Function to add an edge into the graph
    void
                          addEdge(int v, int w) { adj.get(v).add(w); }
 
    // A recursive function used by topologicalSort
    void
                          topologicalSortUtil(int v, boolean visited[],
                             Stack<Integer> stack)
    {
        // Mark the current node as visited.
        visited[v] = true;
        Integer i;
 
        // Recur for all the vertices adjacent
        // to thisvertex
        Iterator<Integer> it = adj.get(v).iterator();
        while (it.hasNext()) {
            i = it.next();
            if (!visited[i])
                topologicalSortUtil(i, visited, stack);
        }
 
        // Push current vertex to stack
        // which stores result
        stack.push(new Integer(v));
    }
 
    // The function to do Topological Sort.
    // It uses recursive topologicalSortUtil()
    void
                          topologicalSort()
    {
        Stack<Integer> stack = new Stack<Integer>();
 
        // Mark all the vertices as not visited
        boolean visited[] = new boolean[V];
        for (int
                          i = 0; i < V; i++)
            visited[i] = false;
 
        // Call the recursive helper
        // function to store
        // Topological Sort starting
        // from all vertices one by one
        for (int
                          i = 0; i < V; i++)
            if (visited[i] == false)
                topologicalSortUtil(i, visited, stack);
 
        // Print contents of stack
        while (stack.empty() == false)
            System.out.print(stack.pop() + " ");
    }
 
    // Driver code
    public
                          static void main(String args[])
    {
        // Create a graph given in the above diagram
        Graph g = new Graph(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);
 
        System.out.println("Following is a Topological "
                           + "sort of the given graph");
        // Function Call
        g.topologicalSort();
    }
}
// This code is contributed by Aakash Hasija

                  

              
            

Python3

              
                
                    # Python program to print topological sorting of a DAG
from collections import defaultdict
 
# Class to represent a graph
                        
 
 
class Graph:
    def
                          __init__(self, vertices):
        self.graph =
                          defaultdict(list)  # dictionary containing adjacency List
        self.V = vertices  # No. of vertices
 
    # function to add an edge to graph
    def
                          addEdge(self, u, v):
        self.graph[u].append(v)
 
    # A recursive function used by topologicalSort
    def
                          topologicalSortUtil(self, v, visited, stack):
 
        # Mark the current node as visited.
        visited[v] = True
 
        # Recur for all the vertices adjacent to this vertex
        for i in
                          self.graph[v]:
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
                        
 
        # Push current vertex to stack which stores result
        stack.append(v)
 
    # The function to do Topological Sort. It uses recursive
    # topologicalSortUtil()
    def
                          topologicalSort(self):
        # Mark all the vertices as not visited
        visited = [False]*self.V
        stack = []
                        
 
        # Call the recursive helper function to store Topological
        # Sort starting from all vertices one by one
        for i in
                          range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
                        
 
        # Print contents of the stack
        print(stack[::-1])  # return list in reverse order
                        
 
 
# Driver Code
if __name__ ==
                          '__main__':
    g = Graph(6)
    g.addEdge(5, 2)
    g.addEdge(5, 0)
    g.addEdge(4, 0)
    g.addEdge(4, 1)
    g.addEdge(2, 3)
    g.addEdge(3, 1)
 
    print("Following is a Topological Sort of the given graph")
 
    # Function Call
    g.topologicalSort()
 
# This code is contributed by Neelam Yadav

                  

              
            

Javascript

              
                
                    // Javascript for the above approach
 
    // This class represents a directed graph
    // using adjacency list representation
    class Graph{
 
        // Constructor
        constructor(v)
        {
            // Number of vertices
            this.V = v
 
            // Adjacency List as ArrayList of ArrayList's
            this.adj = new Array(this.V)
            for (let i = 0 ; i < this.V ; i+=1){
                this.adj[i] = new Array()
            }
        }
 
        // Function to add an edge into the graph
        addEdge(v, w){
            this.adj[v].push(w)
        }
 
        // A recursive function used by topologicalSort
        topologicalSortUtil(v, visited, stack)
        {
            // Mark the current node as visited.
            visited[v] = true;
            let i = 0;
 
            // Recur for all the vertices adjacent
            // to thisvertex
            for(i = 0 ; i < this.adj[v].length ; i++){
                if(!visited[this.adj[v][i]]){
                    this.topologicalSortUtil(this.adj[v][i], visited, stack)
                }
            }
 
            // Push current vertex to stack
            // which stores result
            stack.push(v);
        }
 
        // The function to do Topological Sort.
        // It uses recursive topologicalSortUtil()
        topologicalSort()
        {
            let stack = new Array()
 
            // Mark all the vertices as not visited
            let visited = new Array(this.V);
                        
            for (let i = 0 ; i < this.V ; i++){
                visited[i] = false;
            }
 
            // Call the recursive helper
            // function to store
            // Topological Sort starting
            // from all vertices one by one
            for (let i = 0 ; i < this.V ; i++){
                if (visited[i] == false){
                    this.topologicalSortUtil(i, visited, stack);
                }
            }
 
            // Print contents of stack
            while (stack.length != 0){
                console.log(stack.pop() + " ")
            }
        }
    }
 
    // Driver Code
    var
                          g = new Graph(6)
    g.addEdge(5, 2)
    g.addEdge(5, 0)
    g.addEdge(4, 0)
    g.addEdge(4, 1)
    g.addEdge(2, 3)
    g.addEdge(3, 1)
     
    console.log("Following is a Topological sort of the given graph")
     
    // Function Call
    g.topologicalSort()
     
    // This code is contributed by subhamgoyal2014.

                  

              
            

输出

以下是给定图的拓扑排序
5 4 2 3 1 0

时间复杂度： O(V+E)。上面的算法只是带有额外堆栈的 DFS。所以时间复杂度与DFS辅助空间相同
： O(V)。堆栈需要额外的空间

注意： 这里，我们也可以使用向量来代替堆栈。如果使用向量，则以相反的顺序打印元素以获得拓扑排序。

拓扑排序的应用：

拓扑排序主要用于根据作业之间给定的依赖关系来调度作业。
在计算机科学中，此类应用出现在：
- 指令调度
- 在电子表格中重新计算公式值时公式单元格计算的顺序
- 逻辑综合
- 确定要在 make 文件中执行的编译任务的顺序
- 数据序列化
- 解决链接器中的符号依赖性

相关文章：

卡恩的拓扑排序算法
有向无环图的所有拓扑排序

如果您发现任何不正确的内容，或者如果您想分享有关上述主题的更多信息，请发表评论