归并排序可视化交互式动画版

归并排序 被定义为一种排序算法，其工作原理是将数组划分为更小的子数组，对每个子数组进行排序，然后将已排序的子数组合并在一起以形成最终的排序数组。

简单来说，归并排序的过程就是将数组分成两半，对每一半进行排序，然后将已排序的两半合并在一起。重复这个过程，直到整个数组排序完毕。

归并排序算法

归并排序是如何工作的？

归并排序是一种递归算法，它不断地将数组分成两半，直到无法进一步划分为止，即数组只剩下一个元素（只有一个元素的数组总是已排序）。然后将已排序的子数组合并为一个已排序的数组。

请参阅下图以了解合并排序的工作原理。

插图：

让我们考虑一个数组 arr[] = {38, 27, 43, 10}

最初将数组分成相等的两半：

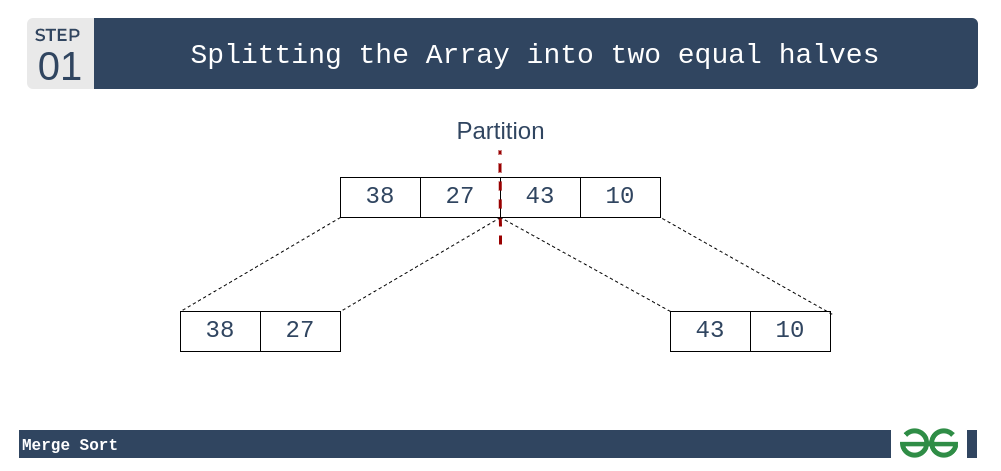
归并排序：将数组分成两半

这些子阵列进一步分为两半。现在它们变成了不能再被分割的单位长度数组，并且单位长度数组总是排序的。

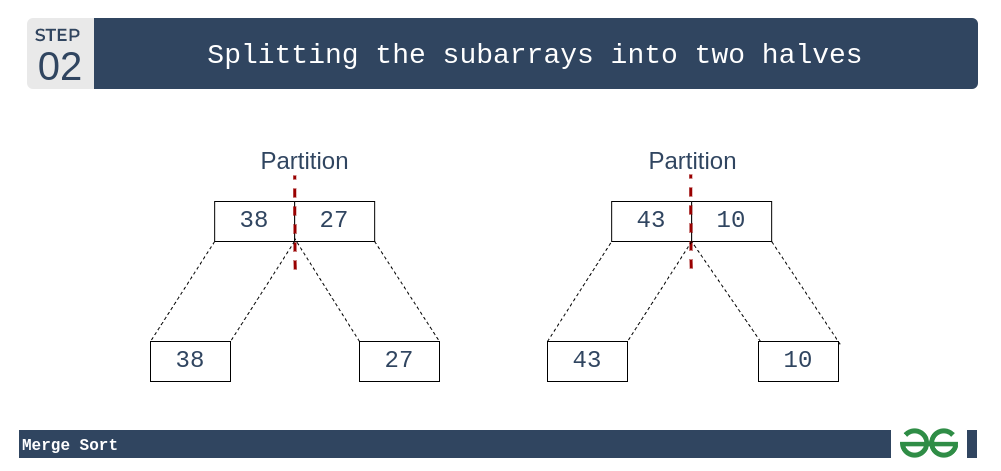
归并排序：将子数组分成两半（这里是单位长度的子数组）

这些排序子数组合并在一起，我们得到更大的排序子数组。

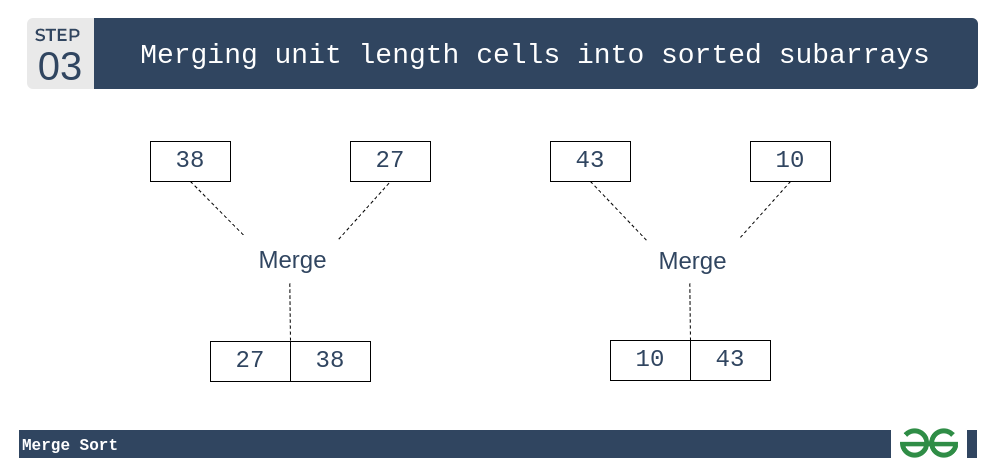
归并排序：将单位长度的子数组合并成已排序的子数组

这个合并过程一直持续到从较小的子数组构建排序数组为止。

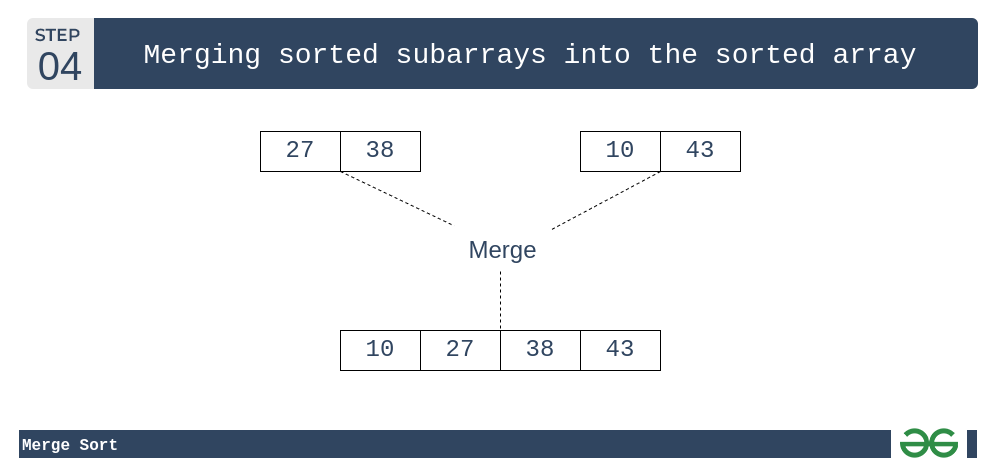
归并排序：将已排序的子数组合并，得到已排序的数组

下图显示了示例数组 {38, 27, 43, 3, 9, 82, 10} 的完整合并排序过程。

下面是归并排序的代码实现。

C++

              
                
                    // C++ program for Merge Sort
#include <bits/stdc++.h>
using namespace std;
 
// Merges two subarrays of array[].
// First subarray is arr[begin..mid]
// Second subarray is arr[mid+1..end]
void merge(int array[], int const left, int const mid,
           int const right)
{
    int
                          const subArrayOne = mid - left + 1;
    int
                          const subArrayTwo = right - mid;
                        
 
    // Create temp arrays
    auto *leftArray = new int[subArrayOne],
         *rightArray = new int[subArrayTwo];
 
    // Copy data to temp arrays leftArray[] and rightArray[]
    for (auto i = 0; i < subArrayOne; i++)
                        
        leftArray[i] = array[left + i];
    for (auto j = 0; j < subArrayTwo; j++)
                        
        rightArray[j] = array[mid + 1 + j];
 
    auto indexOfSubArrayOne = 0, indexOfSubArrayTwo = 0;
    int
                          indexOfMergedArray = left;
 
    // Merge the temp arrays back into array[left..right]
    while (indexOfSubArrayOne < subArrayOne
           && indexOfSubArrayTwo < subArrayTwo) {
        if (leftArray[indexOfSubArrayOne]
                        
            <= rightArray[indexOfSubArrayTwo]) {
            array[indexOfMergedArray]
                = leftArray[indexOfSubArrayOne];
            indexOfSubArrayOne++;
        }
        else {
            array[indexOfMergedArray]
                = rightArray[indexOfSubArrayTwo];
            indexOfSubArrayTwo++;
        }
        indexOfMergedArray++;
    }
 
    // Copy the remaining elements of
    // left[], if there are any
    while (indexOfSubArrayOne < subArrayOne) {
        array[indexOfMergedArray]
            = leftArray[indexOfSubArrayOne];
        indexOfSubArrayOne++;
        indexOfMergedArray++;
    }
 
    // Copy the remaining elements of
    // right[], if there are any
    while (indexOfSubArrayTwo < subArrayTwo) {
        array[indexOfMergedArray]
            = rightArray[indexOfSubArrayTwo];
        indexOfSubArrayTwo++;
        indexOfMergedArray++;
    }
    delete[] leftArray;
    delete[] rightArray;
}
 
// begin is for left index and end is right index
// of the sub-array of arr to be sorted
void mergeSort(int array[], int const begin, int const end)
{
    if
                          (begin >= end)
        return;
 
    int
                          mid = begin + (end - begin) / 2;
    mergeSort(array, begin, mid);
    mergeSort(array, mid + 1, end);
    merge(array, begin, mid, end);
}
 
// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
    for (int i = 0; i < size; i++)
        cout << A[i] << " ";
    cout << endl;
}
 
// Driver code
int main()
{
    int
                          arr[] = { 12, 11, 13, 5, 6, 7 };
    int
                          arr_size = sizeof(arr) / sizeof(arr[0]);
 
    cout << "Given array is \n";
    printArray(arr, arr_size);
 
    mergeSort(arr, 0, arr_size - 1);
 
    cout << "\nSorted array is \n";
    printArray(arr, arr_size);
    return 0;
}
 
// This code is contributed by Mayank Tyagi
// This code was revised by Joshua Estes

                  

              
            

C

              
                
                    // C program for Merge Sort
                        
#include <stdio.h>
                        
#include <stdlib.h>
 
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
                        
{
    int
                          i, j, k;
    int
                          n1 = m - l + 1;
    int
                          n2 = r - m;
 
    // Create temp arrays
    int
                          L[n1], R[n2];
 
    // Copy data to temp arrays L[] and R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
 
    // Merge the temp arrays back into arr[l..r
    i = 0;
                        
    j = 0;
                        
    k = l;
                        
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        }
        else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
 
    // Copy the remaining elements of L[],
    // if there are any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    // Copy the remaining elements of R[],
    // if there are any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}
 
// l is for left index and r is right index of the
// sub-array of arr to be sorted
void mergeSort(int arr[], int l, int r)
                        
{
    if
                          (l < r) {
        int m = l + (r - l) / 2;
 
        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
 
        merge(arr, l, m, r);
    }
}
 
// Function to print an array
void printArray(int A[], int size)
{
    int
                          i;
    for (i = 0; i < size; i++)
        printf("%d ", A[i]);
    printf("\n");
}
 
// Driver code
int main()
{
    int
                          arr[] = { 12, 11, 13, 5, 6, 7 };
    int
                          arr_size = sizeof(arr) / sizeof(arr[0]);
 
    printf("Given array is \n");
    printArray(arr, arr_size);
 
    mergeSort(arr, 0, arr_size - 1);
 
    printf("\nSorted array is \n");
    printArray(arr, arr_size);
    return 0;
}

                  

              
            

Java

              
                
                    // Java program for Merge Sort
import java.io.*;
 
class MergeSort {
 
    // Merges two subarrays of arr[].
    // First subarray is arr[l..m]
    // Second subarray is arr[m+1..r]
    void
                          merge(int arr[], int l, int m, int r)
    {
        // Find sizes of two subarrays to be merged
        int n1 = m - l + 1;
        int n2 = r - m;
 
        // Create temp arrays
        int L[] = new
                          int[n1];
        int R[] = new
                          int[n2];
 
        // Copy data to temp arrays
        for (int
                          i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int
                          j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];
 
        // Merge the temp arrays
 
        // Initial indices of first and second subarrays
        int i = 0, j = 0;
 
        // Initial index of merged subarray array
        int k = l;
        while (i < n1 && j < n2) {
                        
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            }
            else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }
 
        // Copy remaining elements of L[] if any
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }
 
        // Copy remaining elements of R[] if any
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }
 
    // Main function that sorts arr[l..r] using
    // merge()
    void
                          sort(int arr[], int l, int r)
    {
        if (l < r) {
 
            // Find the middle point
            int m = l + (r - l) / 2;
 
            // Sort first and second halves
            sort(arr, l, m);
            sort(arr, m + 1, r);
 
            // Merge the sorted halves
            merge(arr, l, m, r);
        }
    }
 
    // A utility function to print array of size n
    static
                          void printArray(int arr[])
    {
        int n = arr.length;
        for (int
                          i = 0; i < n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver code
    public
                          static void main(String args[])
    {
        int arr[] = { 12, 11, 13, 5, 6, 7 };
 
        System.out.println("Given array is");
        printArray(arr);
 
        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr.length - 1);
 
        System.out.println("\nSorted array is");
        printArray(arr);
    }
}
/* This code is contributed by Rajat Mishra */

                  

              
            

Python3

              
                
                    # Python program for implementation of MergeSort
 
 
def mergeSort(arr):
    if
                          len(arr) > 1:
 
         # Finding the mid of the array
        mid = len(arr)//2
 
        # Dividing the array elements
        L = arr[:mid]
                        
 
        # Into 2 halves
        R = arr[mid:]
                        
 
        # Sorting the first half
        mergeSort(L)
 
        # Sorting the second half
        mergeSort(R)
 
        i = j = k = 0
 
        # Copy data to temp arrays L[] and R[]
        while i < len(L) and
                          j < len(R):
            if L[i] <=
                          R[j]:
                arr[k] = L[i]
                        
                i += 1
            else:
                arr[k] = R[j]
                        
                j += 1
            k += 1
 
        # Checking if any element was left
        while i < len(L):
            arr[k] = L[i]
                        
            i += 1
            k += 1
 
        while j < len(R):
            arr[k] = R[j]
                        
            j += 1
            k += 1
 
 
# Code to print the list
                        
def printList(arr):
    for
                          i in range(len(arr)):
        print(arr[i], end=" ")
    print()
 
 
# Driver Code
if __name__ ==
                          '__main__':
    arr = [12, 11, 13, 5, 6, 7]
    print("Given array is")
    printList(arr)
    mergeSort(arr)
    print("\nSorted array is ")
    printList(arr)
 
# This code is contributed by Mayank Khanna

                  

              
            

C#

              
                
                    // C# program for Merge Sort
                        
using System;
 
class MergeSort {
 
    // Merges two subarrays of []arr.
    // First subarray is arr[l..m]
    // Second subarray is arr[m+1..r]
    void
                          merge(int[] arr, int l, int m, int r)
    {
        // Find sizes of two
        // subarrays to be merged
        int n1 = m - l + 1;
        int n2 = r - m;
 
        // Create temp arrays
        int[] L = new
                          int[n1];
        int[] R = new
                          int[n2];
        int i, j;
 
        // Copy data to temp arrays
        for (i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];
 
        // Merge the temp arrays
 
        // Initial indexes of first
        // and second subarrays
        i = 0;
        j = 0;
 
        // Initial index of merged
        // subarray array
        int k = l;
        while (i < n1 && j < n2) {
                        
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            }
            else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }
 
        // Copy remaining elements
        // of L[] if any
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }
 
        // Copy remaining elements
        // of R[] if any
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }
 
    // Main function that
    // sorts arr[l..r] using
    // merge()
    void
                          sort(int[] arr, int l, int r)
    {
        if (l < r) {
 
            // Find the middle point
            int m = l + (r - l) / 2;
 
            // Sort first and second halves
            sort(arr, l, m);
            sort(arr, m + 1, r);
 
            // Merge the sorted halves
            merge(arr, l, m, r);
        }
    }
 
    // A utility function to
    // print array of size n
    static
                          void printArray(int[] arr)
    {
        int n = arr.Length;
        for (int
                          i = 0; i < n; ++i)
            Console.Write(arr[i] + " ");
        Console.WriteLine();
    }
 
    // Driver code
    public
                          static void Main(String[] args)
    {
        int[] arr = { 12, 11, 13, 5, 6, 7 };
        Console.WriteLine("Given array is");
        printArray(arr);
        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr.Length - 1);
        Console.WriteLine("\nSorted array is");
        printArray(arr);
    }
}
 
// This code is contributed by Princi Singh

                  

              
            

Javascript

              
                
                    // JavaScript program for Merge Sort
 
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
function merge(arr, l, m, r)
{
    var
                          n1 = m - l + 1;
    var
                          n2 = r - m;
 
    // Create temp arrays
    var
                          L = new Array(n1); 
    var
                          R = new Array(n2);
 
    // Copy data to temp arrays L[] and R[]
    for
                          (var i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for
                          (var j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
 
    // Merge the temp arrays back into arr[l..r]
 
    // Initial index of first subarray
    var
                          i = 0;
 
    // Initial index of second subarray
    var
                          j = 0;
 
    // Initial index of merged subarray
    var
                          k = l;
 
    while
                          (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        }
        else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
 
    // Copy the remaining elements of
    // L[], if there are any
    while
                          (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    // Copy the remaining elements of
    // R[], if there are any
    while
                          (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}
 
// l is for left index and r is
// right index of the sub-array
// of arr to be sorted
                        
function mergeSort(arr,l, r){
    if(l>=r){
        return;
    }
    var
                          m =l+ parseInt((r-l)/2);
    mergeSort(arr,l,m);
    mergeSort(arr,m+1,r);
    merge(arr,l,m,r);
}
 
// Function to print an array
function printArray( A, size)
{
    for
                          (var i = 0; i < size; i++)
       console.log(  A[i] + " ");
}
 
 
var arr = [ 12, 11, 13, 5, 6, 7 ];
    var
                          arr_size = arr.length;
 
    console.log(  "Given array is ");
    printArray(arr, arr_size);
 
    mergeSort(arr, 0, arr_size - 1);
 
    console.log( "Sorted array is ");
    printArray(arr, arr_size);
 
// This code is contributed by SoumikMondal

                  

              
            

PHP

              
                
                    <?php
/* PHP recursive program for Merge Sort */
 
// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
function merge(&$arr, $l, $m, $r)
{
    $n1
                          = $m - $l + 1;
                        
    $n2
                          = $r - $m;
 
    // Create temp arrays
    $L
                          = array();
                        
    $R
                          = array();
                        
   
                        
    // Copy data to temp arrays L[] and R[]
    for
                          ($i = 0; $i < $n1; $i++)
        $L[$i] = $arr[$l + $i];
    for
                          ($j = 0; $j < $n2; $j++)
        $R[$j] = $arr[$m + 1 + $j];
 
    // Merge the temp arrays back into arr[l..r]
    $i
                          = 0;
    $j
                          = 0;
    $k
                          = $l;
                        
    while
                          ($i < $n1 && $j < $n2) {
                        
        if ($L[$i] <= $R[$j]) {
            $arr[$k] = $L[$i];
            $i++;
        }
        else {
            $arr[$k] = $R[$j];
            $j++;
        }
        $k++;
    }
 
    // Copy the remaining elements of L[], 
    // if there are any
    while
                          ($i < $n1) {
                        
        $arr[$k] = $L[$i];
        $i++;
        $k++;
    }
 
    // Copy the remaining elements of R[], 
    // if there are any
    while
                          ($j < $n2) {
                        
        $arr[$k] = $R[$j];
        $j++;
        $k++;
    }
}
 
// l is for left index and r is right index of the
// sub-array of arr to be sorted
function mergeSort(&$arr, $l, $r)
{
    if
                          ($l < $r) {
                        
        $m = $l
                          + (int)(($r - $l) / 2);
                        
 
        // Sort first and second halves
        mergeSort($arr, $l, $m);
        mergeSort($arr, $m + 1, $r);
                        
 
        merge($arr, $l, $m, $r);
    }
}
 
// Function to print an array
function printArray($A, $size)
{
    for
                          ($i = 0; $i < $size; $i++)
        echo $A[$i]." ";
    echo
                          "\n";
}
 
// Driver code
$arr = array(12, 11, 13, 5, 6, 7);
$arr_size = sizeof($arr);
 
echo "Given array is \n";
printArray($arr, $arr_size);
 
mergeSort($arr, 0, $arr_size - 1);
 
echo "\nSorted array is \n";
printArray($arr, $arr_size);
return 0;
 
//This code is contributed by Susobhan Akhuli
?>

                  

              
            

输出

给定数组是
12 11 13 5 6 7
排序后的数组是
5 6 7 11 12 13

归并排序的复杂度分析：

时间复杂度： O(N log(N))，归并排序是一种递归算法，时间复杂度可以表示为以下递归关系。

T(n) = 2T(n/2) + θ(n)

上述递归可以使用递归树方法或主方法来解决。属于主方法的情况II，递推解为θ(Nlog(N))。在所有 3 种情况（最差、平均和最佳）下，归并排序的时间复杂度均为 θ(Nlog(N))，因为归并排序始终将数组分为两半，并且需要线性时间来合并两半。

辅助空间： O(N)，在合并排序中，所有元素都复制到辅助数组中。所以归并排序需要N个辅助空间。

归并排序的应用：

对大型数据集进行排序： 合并排序特别适合对大型数据集进行排序，因为它保证最坏情况的时间复杂度为 O(n log n)。
外部排序： 归并排序常用于外部排序，当待排序的数据太大而无法放入内存时。
自定义排序： 合并排序可以适应处理不同的输入分布，例如部分排序、接近排序或完全未排序的数据。
倒数计数问题

归并排序的优点：

稳定性 ：归并排序是一种稳定的排序算法，这意味着它保持输入数组中相等元素的相对顺序。
保证最坏情况下的性能： 归并排序的最坏情况时间复杂度为 O(N logN)，这意味着即使在大型数据集上它也能表现良好。
可并行化 ：合并排序是一种天然可并行化的算法，这意味着它可以轻松并行化以利用多个处理器或线程。

归并排序的缺点：

空间复杂度： 归并排序在排序过程中需要额外的内存来存储合并后的子数组。
非就地： 合并排序不是就地排序算法，这意味着它需要额外的内存来存储排序后的数据。这对于关注内存使用的应用程序来说可能是一个缺点。
对于小数据集并不总是最佳的： 对于小数据集，合并排序比其他一些排序算法（例如插入排序）具有更高的时间复杂度。这可能会导致非常小的数据集的性能降低。

快速链接：

关于合并排序的最新文章
排序的编码练习。
归并排序测验