顺序查找-乱序表 可视化交互式动画版
线性搜索，顺序查找
被定义为一种顺序
搜索算法
，从一端开始，遍历列表中的每个元素，直到找到所需的元素，否则搜索将继续，直到数据集的末尾。
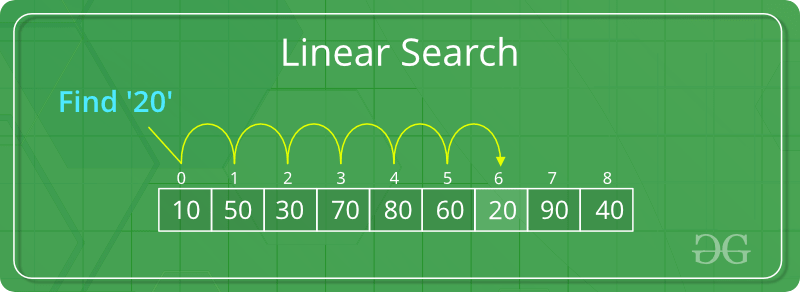
线性搜索，顺序查找算法
线性搜索，顺序查找算法如何工作？
在线性搜索，顺序查找算法中，
-
每个元素都被视为该键的潜在匹配项并进行相同检查。
-
如果找到任何元素等于该键，则搜索成功并返回该元素的索引。
-
如果没有找到与键相等的元素，则搜索结果为“未找到匹配项”。
例如：
考虑数组
arr[] = {10, 50, 30, 70, 80, 20, 90, 40}
且
key
= 30
步骤1：
从第一个元素（索引0）开始，将
key
与每个元素（arr[i]）进行比较。
-
将 key 与第一个元素 arr[0] 进行比较。
由于不相等，迭代器将移动到下一个元素作为潜在的匹配项。
![将 key 与 arr[0] 进行比较](https://media.geeksforgeeks.org/wp-content/uploads/20230519161339/Linear-search-algorithm-1.webp)
将 key 与 arr[0] 进行比较
-
将 key 与下一个元素 arr[1] 进行比较。
由于不相等，迭代器将移动到下一个元素作为潜在的匹配项。
![将 key 与 arr[1] 进行比较](https://media.geeksforgeeks.org/wp-content/uploads/20230519161415/Linear-search-algorithm-2.webp)
将 key 与 arr[1] 进行比较
步骤2：
现在，当将arr[2]与key进行比较时，值匹配。
因此，线性搜索，顺序查找算法将产生一条成功消息，并在找到 key 时返回元素的索引（此处为 2）。
![将 key 与 arr[2] 进行比较](https://media.geeksforgeeks.org/wp-content/uploads/20230519161442/Linear-search-algorithm-3.webp)
将 key 与 arr[2] 进行比较
线性搜索，顺序查找算法的实现：
下面是线性搜索，顺序查找算法的实现：
-
C
-
C++
-
Java
-
Python3
-
C＃
-
PHP
-
JavaScript
C
#include <stdio.h>
int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++)
if (arr[i] == x)
return i;
return -1;
}
int main(void)
{
int
arr[] = { 2, 3, 4, 10, 40 };
int
x = 10;
int
N = sizeof(arr) / sizeof(arr[0]);
int
result = search(arr, N, x);
(result == -1)
? printf("Element is not present in array")
: printf("Element is present at index %d", result);
return 0;
}
|
C++
#include <bits/stdc++.h>
using namespace std;
int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++)
if (arr[i] == x)
return i;
return -1;
}
int main(void)
{
int
arr[] = { 2, 3, 4, 10, 40 };
int
x = 10;
int
N = sizeof(arr) / sizeof(arr[0]);
int
result = search(arr, N, x);
(result == -1)
? cout << "Element is not present in array"
: cout << "Element is present at index " << result;
return 0;
}
|
Java
import java.io.*;
class GFG {
public
static int search(int arr[], int N, int x)
{
for (int
i = 0; i < N; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
public
static void main(String args[])
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int result = search(arr, arr.length, x);
if (result == -1)
System.out.print(
"Element is not present in array");
else
System.out.print("Element is present at index "
+ result);
}
}
|
Python3
def search(arr, N, x):
for
i in range(0, N):
if (arr[i] == x):
return i
return
-1
if __name__ ==
"__main__":
arr = [2, 3, 4, 10, 40]
x = 10
N = len(arr)
result = search(arr, N, x)
if(result ==
-1):
print("Element is not present in array")
else:
print("Element is present at index", result)
|
C#
using System;
class GFG {
public
static int search(int[] arr, int N, int x)
{
for (int
i = 0; i < N; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
public
static void Main()
{
int[] arr = { 2, 3, 4, 10, 40 };
int x = 10;
int result = search(arr, arr.Length, x);
if (result == -1)
Console.WriteLine(
"Element is not present in array");
else
Console.WriteLine("Element is present at index "
+ result);
}
}
|
PHP
<?php
function search($arr, $n, $x)
{
for($i = 0; $i < $n; $i++) {
if($arr[$i] == $x)
return $i;
}
return
-1;
}
$arr = array(2, 3, 4, 10, 40);
$x = 10;
$result = search($arr, sizeof($arr), $x);
if($result == -1)
echo
"Element is not present in array";
else
echo
"Element is present at index " ,
$result;
?>
|
Javascript
function search(arr, n, x)
{
for
(let i = 0; i < n; i++)
if (arr[i] == x)
return i;
return
-1;
}
let arr = [ 2, 3, 4, 10, 40 ];
let x = 10;
let n = arr.length;
let result = search(arr, n, x);
(result == -1)
? console.log("Element is not present in array")
: console.log("Element is present at index " + result);
|
线性搜索，顺序查找的复杂度分析：
时间复杂度：
-
最佳情况：
在最好的情况下，键可能出现在第一个索引处。
所以最好的情况复杂度是 O(1)
-
最坏的情况：
在最坏的情况下，键可能出现在最后一个索引处，即与列表中开始搜索的末尾相反的位置。
因此，最坏情况的复杂度是 O(N)，其中 N 是列表的大小。
-
平均情况：
O(N)
辅助空间：
O(1)，因为除了迭代列表的变量之外，没有使用其他变量。
线性搜索，顺序查找的优点：
-
无论数组是否已排序，都可以使用线性搜索，顺序查找。
它可以用于任何数据类型的数组。
-
不需要任何额外的内存。
-
它是一种非常适合小型数据集的算法。
线性搜索，顺序查找的缺点：
-
线性搜索，顺序查找的时间复杂度为 O(N)，这反过来又使得大型数据集的搜索速度变慢。
-
不适合大型阵列。
什么时候使用线性搜索，顺序查找？
-
当我们处理小数据集时。
-
当您搜索存储在连续内存中的数据集时。